LТехнические науки. Автоматизированные системы управления на производстве

Садыков Р., Золотов А., Степанова О.

Семипалатинский государственный университет имени Шакарима,

г. Семей

РАЗРАБОТКА системы управления лесосушильной камеры на основе математической модели процесса

Организация автоматического управления сушкой древесины должна осуществляться с позиции энергетической эффективности. При этом целесообразно решить задачу синтеза оптимального закона управления отдельным агрегатом сушки древесины с позиции определенного критерия оптимальности при соблюдении требований технологии, но формулирование критерия и построение модели не рассматриваются разработчиками как единый процесс. Это приводит к серьезным затруднениям при решении задач оптимального управления и созданию управляющих устройств, закон функционирования которых практически мало учитывает свойства объектов управления. Желательно, чтобы критерий давал возможность аналитического решения задачи оптимального управления.

Ключевым этапом в разработке системы управления на базе УВК считается создание математической модели процесса, которая представляет собой основу алгоритмов контроля и управления. Главным требованием, предъявляемым к математической модели, является отражение тех сторон функционирования лесосушильных камер, знание которых необходимо для управления этими камерами, т.е. цель математического описания лесосушильных камер заключается в разработке алгоритма управления, хотя желательно, чтобы модель можно было применить и для поиска оптимальных технологических режимов на стадии проектирования сушильных агрегатов [1]. Разработка модели включает три этапа [2]. Первый этап - построение теоретической аналитической модели, обеспечивающей качественную сходимость с процессом. На втором этапе вводится простейший алгоритм адаптации и оценивается адекватность модели процессу. На третьем этапе на основании длительной экспериментальной проверки дрейфа параметров модели совершенствуется алгоритм адаптации.

Рассмотрим лесосушильную камеру как объект регуляции температуры агента сушки.

Количество тепла, Q, которое передается от калорифера в камеру за время dt, определяется уравнением теплового баланса:

,

(1)

где K_K – коэффициент теплопередачи;

F_K – поверхность калорифера;

Q_П и Q_С – температуры пара в калорифере и агента сушки в камере.

Рассматривая динамику объекта по каналу «температура пара - температура агента сушки в камере», допускают, что температура агента сушки по объему одинаковая и отклонения температуры пара небольшие: Q_П= Q_П.О. ± ∆_П.

Тепло, переданное в камеру от калорифера за бесконечно малый промежуток времени dt, тратится на:

- нагревание калорифера: ;

- металла в камере: ;

- покрытие потерь: ;

- теплообмен с древесиной: .

Уравнение теплового баланса запишется:

(2)

где с_М – теплоемкость металла;

Т_К – масса металла в камере;

F_ОГ – поверхность ограждений;

Q_НАР – температура внешней среды;

k_ОГ – средний коэффициент теплопередачи ограждений;

α – коэффициент теплоотдачи в процессе сушки;

F_Д – поверхность древесины;

Q_Д – температура древесины.

В установленном режиме, когда dQ_К/dt=0, уравнение (2) будет иметь вид:

(3)

(4)

Если: , тогда при ΔQ_к=ΔQ_П и уравнение (4) примет вид:

; ,

(5)

где Т – постоянная времени.

Из уравнения (5) очевидно, что по каналу «температура пара – температура агента сушки» в камере объект является инерционным звеном.

Рассмотренная математическая модель не учитывает время запаздывания в реальных условиях. Поэтому модель можно записать в общем виде:

,

(6)

Таким образом, камера периодического действия может быть представлена последовательным включением апериодического звена и звена чистого запаздывания.

При выводе уравнений принимаем, что при малых изменениях температуры агента сушки в камере, за короткие промежутки времени, температура древесины остается постоянной. В этом случае теплоемкость не оказывает влияния на инерционность камеры [2].

В первом приближении объект регулирования ОР (вакуумная камера) описывается передаточной функцией:

,

(7)

где k_об – коэффициент передачи объекта;

τ₀ – запаздывание объекта;

Т – постоянная времени объекта.

Рассчитаем k_об, используя формулу (3):

,

(8)

Тогда = 0,21.

Постоянная времени объекта будет равна:

,

(9)

тогда =2,73.

Согласно характеристик лесосушильной камеры [2] отношение:

, тогда

В системе регулирования, согласно методики [3] выбираем непрерывный ПИ-регулятор.

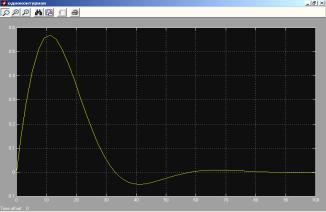
Параметры регулятора рассчитываем с помощью среды MATLAB. Введя рассчитанные в уравнениях (8) и (9) коэффициенты в соответствующие блоки получили переходную характеристику, изображенную на рисунке 1.

Рисунок 1.

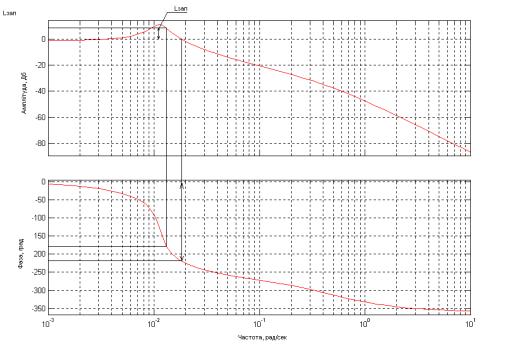
Проведем исследование запаса устойчивости системы по амплитуде и фазе. Для этого в среде MATLAB построим графики АЧХ и ФЧХ системы (рисунок 2).

Рисунок 2. АЧХ и ФЧХ системы

Из построенных графиков видно, что запас устойчивости по амплитуде составляет: L_зап=10 Дб, а запас устойчивости по фазе: L_зап=220 градусов. Данные значения превышают минимально допустимые, а потому можно сказать, что система является устойчивой.

Литература:

1. Расев А.И. Сушка древесины: Учебное пособие. Изд. 4-е. – М.: МГУЛ, 2000. - 178 с.

2. Гостев В.И. Системы управления с цифровыми регуляторами. Справочник. – Киев.: Техника, 1990. - 280 с.

3. Емельянов А.И., Капник О.В. Проектирование систем автоматизации технологических процессов. Справочное пособие. 3-е изд. перераб. и доп. – М.: Энергоатомиздат, 1983. - 399 с.
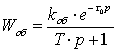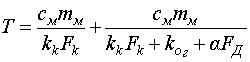