Технические науки/6. Электротехника и радиоэлектроника

Ст. преп. Мирзакулова Ш.А., ст. преп. Балгабекова Л.О.

Алматинский университет энергетики и связи

ИССЛЕДОВАНИЕ СЕТЕВОГО ТРАФИКА НА САМОПОДОБИЕ МЕТОДОМ АБСОЛЮТНЫХ МОМЕНТОВ

Согласно теории телетрафика – природа сетевого трафика соответствует Пуассоновскому процессу и промежуток времени между произвольными двумя соседними событиями распределен по показательному закону. Начиная с 1993 года, после публикации результатов исследований структуры сетевого трафика американскими учеными W.Leland, M.Taqqu, W.Willinger и D.Wilson появилась проблема самоподобия. Количество исследований и измерений характеристик сетевого трафика растет, что свидетельствует о ее актуальности. Свойство самоподобия характеризуется тем, что при изменении шкалы измерений корреляционная структура рассматриваемого самоподобного процесса не изменяется.

В работе [1] В.И. Нейман определил, что самоподобный процесс выражен в медленном убывании дисперсии, долговременной зависимости и флуктуационном характере спектра мощности таких процессов.

Для оценивания степени самоподобия трафика в сети был введен параметр Херста (Hurst), обозначаемый буквой «Н». При Н=0,5 самоподобие отсутствует. А значения Н близкие к единице соответствуют высокой степени самоподобия процесса. Существует ряд методов оценивания параметра Херста и все они отличаются друг от друга сложностью вычислений и точностью получаемого результата. Среди них метод абсолютных моментов дает достаточно точные результаты [2].

Исследуем статистические свойства распределения пакетов (временной ряд) однородного потока протокола ARP и осуществим оценку степени самоподобия трафика с применением метода абсолютных моментов [2].

В течение пяти часов измерен сетевой трафик в режиме реального времени, за это время отслежено 493 пакета протокола ARP, вычислены числовые значения распределения этой случайной величины (таблица 1).

Таблица 1 – Числовые характеристики случайной величины

Наименование	Значение
Математическое ожидание	1,165
Дисперсия	3,254
Среднеквадратическое отклонение	1,8
Коэффициент вариации	1,55

На основании данных таблицы 1 видно, что измеренный трафик не обладает свойствами простейшего потока (пуассоновского) пакетов. На рисунке 1 показано распределение количества пакетов протокола ARP в единицу времени, на которой видно неравномерность интенсивности поступления пакетов и пульсирующий характер трафика с наличием всплесков.

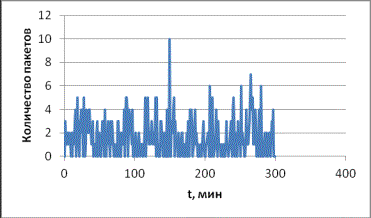
Рисунок 1 – Распределение числа пакетов ARP в единицу времени

При сравнительно небольшом среднем значении поступления пакетов имеются пиковые значения. Для приведенного трафика математическое ожидание числа пакетов составляет 1,64 на интервале 300 минут, а пиковые значения достигают 6, 7 и выше (10 пакетов). Соответственно дисперсия и среднеквадратическое отклонение равны 4,39 и 2,095. На рисунке 2 показано распределение вероятностей интервалов между пакетами ARP. Для оценки степени самоподобия трафика методом абсолютных моментов исходная последовательность длиной N разделяется на блоки с длиной m.

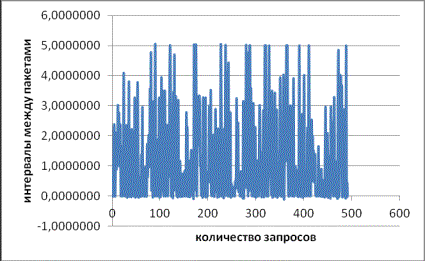
Рисунок 2 – Распределение интервалов между пакетами ARP

Для каждого блока рассчитывается дисперсия и математическое ожидание:

(1)

После этого для каждого блока находился n-й момент.

(2)

Далее строится график зависимости средних значений (дисперсий) абсолютных моментов для последовательности от m. С помощью полученных точек построена аппроксимирующая прямая (рисунок 3). экспериментальных данных.

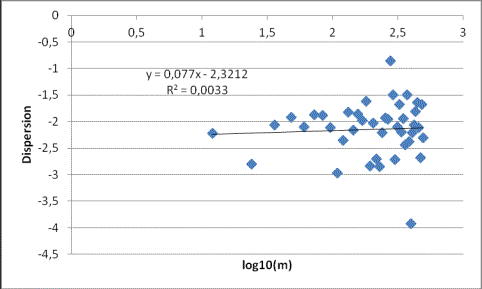
Рисунок 3 – Дисперсионно-временной график

Получившийся наклон линии равен β. С помощью β найден коэффициент самоподобности H= 1−β=1-0,077=0,923.

В результате исследования было выявлено, что измеренный трафик протокола ARP обладает свойствами самоподобия. Чем ближе H к 1, тем больше процесс самоподобен.

Литература:

1 В.И. Нейман, Самоподобные процессы и их применение в теории телетрафика //Тр.МАС. – 1999. - №1(9). – С. 1-15.

2 О. И. Шелухин, А.М. Тенякшев, А.В. Осин Моделирование информационных систем. Учебное пособие. – М.: Радиотехника, 2005. – 368с.