Dr. Sc. Vitrenko
V.A.
Postgraduate
Kashura M.A.
East Ukrainian
National University V. Dahl
Simulation of temperature processes in the
interaction gear teeth with teeth screw hyperboloid lap
Introduction. Modern manufacturing process gear
manufacturer must provide details of relevant operating conditions and accuracy
requirements at minimum cost. The main factors affecting the choice of the
process are: the design and size of gear; procurement type and material,
requirements for accuracy and heat treated wheels and the volume of
production. The proper assignment of the cutting for machining has a big
impact on the quality of the machined surface.
One of the parameters that accompany the process
of treatment and affects quality is the temperature that occurs between the
surface of the treated parts and tools. The high temperature exposure can
lead to the burn marks, deformation work surface, micro-cracking, etc.
Contact temperature is of interest to study, because influence
the quality of the treated surface [12].
The purpose of the article. Construct a mathematical
model and calculate the temperature encountered in the processing of the tooth
spur gear screw hyperboloidal lap.
The main part. Consider the circuit grinding gear teeth
helical hyperboloid lap as the transfer to the crossed axes, where the lap
rotates on its axis and performs translational motion with supply S, the gear
rotates around the axis (Fig. 1). The equation of the relative sliding
velocity can be written as follows:
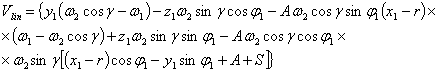(1)
Fig. 1. Diagram of teeth grinding spur
gear screw hyperboloid lap.
To determine the contact cutting temperature
should consider the example of the interaction of the surface of the tooth with
the gear tooth surface tool (lap pressed to the wheel with the force of the
treated S d and rotate with a certain angular velocity ω, the relative
sliding velocity V lin) (Fig. 2).
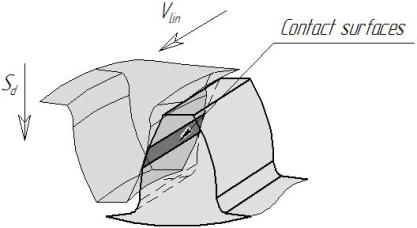
Fig. 2. Scheme contact surfaces
treated tooth and the tooth wheel of lap
Under the force of Sd, by the
elasticity of the materials and tools produced wheel contact patch, which has a
rectangular shape. The image size of the contact area of the surface of
lap and gear can be determined by the formulas of the theory of elasticity [9].
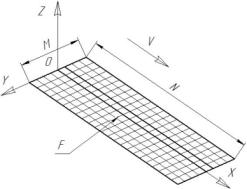
Contact pattern (area F) can be represented as a
set of rods with insulated side walls (Fig. 3).
|
Fig. 3. The scheme of the contact. |
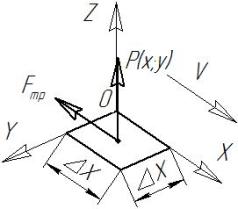
Fig. 4. Scheme at the direction of the
forces. |
At each point of the contact forces are
presented in Fig. 4, which 
is the force of friction -
friction 
- normal load acting, 
at the center of each cell and the contact is defined as the product of
voltage in each cell of the contact in their area.
To determine the voltage 
at each point of contact area used
formula by Hertz.
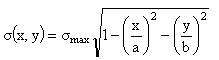, (2)
where - the maximum voltage in the center of the
contact patch.
In this scheme contact gear screw hyperboloidal
lap, the maximum tension 
can be defined by the formula [9]:
. (3)
where 
the coefficient, the value of
which is determined by the table [9], page 642.
The temperature at the surface of the rod,
located in the contact area can be determined by the example of a semi-infinite
body heated by a heat flux of constant power [11]. Temperature distribution
over the thickness of the body at any given time is determined by the formula:
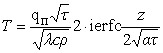(4)
in this case the function, hence the expression
(4) will be:
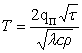(5)
where:
-thermal conductivity, c - specific heat, and 
the density [12], 
the contact time, duration of
exposure to the heat source to the point half - cell length of the contact,
which is equal to the surface grid step along the x-axis (Fig. 4).
- heat flux on the surface of cells of the contact, which can be determined
from:
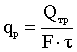(6)
where
F - the contact area of the cell;
- the amount of heat that results from the work of friction forces at the
time 
, determined from the expression:
(7)
where 
is the coefficient of heat flux
distribution (assuming equal to 0.5 [14]).
- power of friction is determined from (7):
. (8)
In the simulation process, contact temperatures
grinding gear made of steel St35, screw hyperboloid lap made of cast iron GG20,
the calculation is performed in turn for each m-th band of the contact. The
initial temperature distribution along the length of the rod is considered
known and equal to zero, and the power for the time 
constant of the heat source. After the calculation of the temperature
at the end of the first to the direction of travel of the rod from the heat
source 
in the course of time 
, a transition to the next bar. At the second bar for the same period
of time effective heat source 
(the value of which is determined
as the difference between the temperature-induced source 
(for the time 
- passed two bars) and
temperature on the action of the same power source 
for the time 
). Thus calculated the temperature change in the core of the change in
temperature 
and additive, which occurred after
the end of the source 
through time 
. Thus computations were performed M times, followed by a transition
to the consideration of the next strip contact, examination, which for the
first while moving the rod again take zero initial conditions.
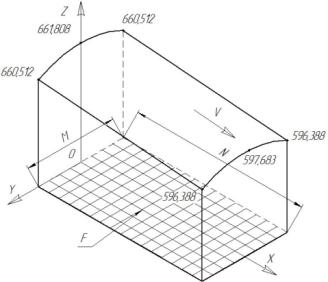
Research results. The calculation by the present model, the
values of temperature (Fig. 5) (relative sliding velocity Vlin =
0.256 m/s, a pressing force P = 100 N).
Temperature occurs on the surface of cells of
the contact gear tooth reaches 661 C.
Fig. 5. The temperature field on the
surface of the contact
Conclusions. Based on the processing method of
teeth spur gears helical hyperboloidal lap the technique of calculating the
temperature in the treatment area, with which you can select the optimal modes
grinding, allows get high precision and avoid burn marks, deformation work
surface and microcracks.
References: 1. Abrasive and diamond material
processing: Directory / [A.N. Reznikov, E.I. Aleksentsev,
M.I. Barat] - Mashinostroenie, 1977. - 391 p.
2. Vitrenko A.V. Finishing and
hardening treatment tooth spur gears / A.V. Vitrenko, I.A. Kirichenko
// Reliability tools and optimization of systems: a collection of research
papers. - Kramatorsk, 2007. - Vyp.21. - S. 202 - 206.
3. Vitrenko O.S. Increasing the
accuracy of the hardening of teeth rolling through the development of
fundamentally new geometry technology:
Dis. Candidate. tech. Science / VNU them. V.Dal,
2010.
4. Lashnev S.I. Shaping and gear parts
blockboards we worm tools / S.I. Lashnev. - Mashinostroenie,
1971. - 215 p.
5. N.I. Kolchin. Methods for
calculating the production and control gear products / N.I. Kolchin,
F.L. Litvin. - L: Mechanical Engineering, 1952. - 269 p.
6. Markeev A.P. Engineering mechanics:
A Textbook for universities. - Moscow: CheRo, 1999 - 572 p.
7. Manufacture of gears: Directory /
[S.N. Kalashnikov, A.S. Kalashnikov, G.I. Kogan and others];
under red. B.A. Thais. - [3rd ed., Rev. and add.]. -
Mashinostroenie, 1990. - 464.
8. Guide to the strength of materials /
G.S. Pisarenko, A.P. Yakovlev, V.V. Matveyev, Ed. G.S.
Pisarenko -2nd ed., Rev. And add. - Kiev: Nauk. Dumka, 1988.-736
p. - ISBN 5-12-000299-4.
9. Goldfarb E.M. Heat engineering
metallurgical processes. - Moscow, Metallurgy, 1967. - 439 p.
10. Calculation and study of friction
during braking / A.V. Chichinadze. -M.: Science, 1967.
11. Sheveleva G.I. The theory of
morphogenesis and contact of moving bodies. Monograph / G.I.
Sheveleva. - Moscow: Stankin, 1999. - 494 p.
12. Basov G.G. / To the calculation of
temperature on the surface of spot of comb of wheel with the lateral surface of
head of rail //, Gorbunov N.I., Popov S.V. IV International congress
"Mechanical engineering technologies` 04. " Sofia. - Year
XI, Volume 8/76, September 2004. - Section 6, p. 133-135.
13. Manufacturing Processes 2. Fritz Klocke,
Aaron Kuchle, RWTH edition Engineering (Springer-11647) Springer, 2009 p. 433.
14. Influence of
surface condition on the fatigue behaviour of specimens made of a SAE 5115
case-hardened steel. S. Laue, H. Bomas., F. Hoffmann. Fatigue & Fracture of
Engineering Materials & Structures. Volume 29, Issue 3, pages 229–241,
March 2006.