Экология/3.Радиационная
безопасность и социально-экологические проблемы
Д.ф.-м.н. Бутусов О.Б.1, чл.-корр. РАН, д.т.н. Мешалкин В.П.2,3,
к.т.н. Редикульцева Н.И.1, д.э.н. Белозерский А.Ю.2
1Московский
государственный машиностроительный университет (МАМИ),
2Российский
химико-технологический университет им. Д.И.Менделеева
3Институт
общей и неорганической химии им. Н.С.Курнакова РАН
Математическое моделирование
распространения радиоактивных загрязнений при разрушении хранилищ радиоактивных
отходов
Разработаны многоуровневая нечетко-дифференциальная модель распространения радиоактивных загрязнений (РЗ) в геологических слоях с учетом неопределенности и алгоритм решения системы нечетко-дифференциальных уравнений модели, основанный на представлении нечетких интервальных переменных с помощью центров и длин интервалов неопределенности. В настоящее время проблема обеспечения безопасности геологических хранилищ радиоактивных отходов (РАО) имеет актуальное значение в связи с развитием мощностей атомной энергетики, что приводит к постоянному росту и накоплению количества РАО. На сегодняшний день признано (в том числе и МАГАТЭ), что наиболее эффективным и безопасным решением проблемы окончательного захоронения РАО является их захоронение в могильниках на глубине не менее 300-500 м в глубинных геологических формациях с соблюдением принципа многобарьерной защиты и обязательным переводом жидких радиоактивных отходов в твердое состояние. Однако, несмотря на принятые меры хранилища РАО не являются абсолютно надежными. Разрушения геологических хранилищ РАО обусловлены образованием разломов, трещин или зон дробления слоев горных пород, которые приводят к изменениям изоляционных, сорбционных и теплофизических свойств различных блоков горных пород, в которых размещены хранилища. Разрушение, или разгерметизация, хранилищ РАО во многом обусловлена выделением большого количества теплоты в результате протекания радиоактивных реакций в хранилищах, при этом выделение теплоты в РАО существенно влияет на величину периода герметичности хранилища [1-3]. При разгерметизации хранилища РАО вода, находящаяся в микротрещинах горных пород, просачивается внутрь хранилища, а затем вместе с растворенными в ней РЗ диффундирует в обратном направлении. Далее в результате диффузии происходит перенос радиоактивных загрязнений в различных направлениях, в том числе и к земной поверхности. В зарубежной литературе скорость диффузии РЗ получила термин «скорость вытекания». Вместе с периодом герметизации хранилища эти две характеристики являются наиболее неопределенными. Для их моделирования также как в [4] были использованы интервальные числа. Неопределенность физико-химических параметров геологической среды была частично компенсирована использованием многоуровневой модели. Для математического описания распространения РЗ в геологических слоях использована следующая многоуровневая система интервальных дифференциальных уравнений в частных производных
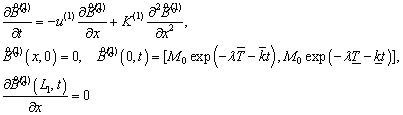
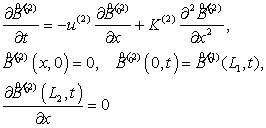 (1)
(1)
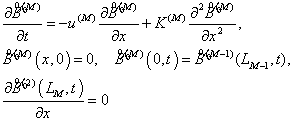
где ![]() - концентрация РЗ в m-м
геологическом слое;
- концентрация РЗ в m-м
геологическом слое; ![]() скорость адвекции РЗ в m-м
геологическом слое,
скорость адвекции РЗ в m-м
геологическом слое, ![]() - коэффициент диффузии в m-м
геологическом слое, λ – постоянная радиоактивного распада. Основными
источниками неопределенности приняты следующие параметры: T – период
герметичности, k – скорость вытекания РЗ из
хранилища. В качестве граничных условий использованы условия сопряжения
концентраций РЗ на границах слоев. Волнистая черта сверху обозначает
интервальное число, обычная черта снизу и сверху обозначает соответственно
нижнюю и верхнюю границы интервального числа. В первой краевой задаче системы
(1) использована экспоненциальная модель диффузии РЗ из источника загрязнения.
- коэффициент диффузии в m-м
геологическом слое, λ – постоянная радиоактивного распада. Основными
источниками неопределенности приняты следующие параметры: T – период
герметичности, k – скорость вытекания РЗ из
хранилища. В качестве граничных условий использованы условия сопряжения
концентраций РЗ на границах слоев. Волнистая черта сверху обозначает
интервальное число, обычная черта снизу и сверху обозначает соответственно
нижнюю и верхнюю границы интервального числа. В первой краевой задаче системы
(1) использована экспоненциальная модель диффузии РЗ из источника загрязнения.
Для численного решения системы интервальных дифференциальных краевых задач (1) использована полностью неявная вычислительная схема с разностями против потока. При этом уравнения m-й краевой задачи с помощью операций интервальной алгебры приводятся к системе уравнений для границ интервалов неопределенности:
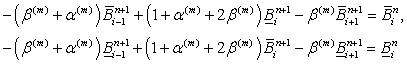 (2)
(2)
где ![]() ,
i - индекс пространственного узла и n - индекс временного слоя. Система
алгебраических уравнений (2) имеет шестидиагональную матрицу. Для упрощения
задачи предложено привести систему уравнений (2) к двум независимым системам
уравнений с трехдиагональными матрицами, для чего вместо нижних и верхних
границ интервалов неопределенности использованы центры и длины этих интервалов:
,
i - индекс пространственного узла и n - индекс временного слоя. Система
алгебраических уравнений (2) имеет шестидиагональную матрицу. Для упрощения
задачи предложено привести систему уравнений (2) к двум независимым системам
уравнений с трехдиагональными матрицами, для чего вместо нижних и верхних
границ интервалов неопределенности использованы центры и длины этих интервалов:
![]() .
При этом границы интервалов могут быть рассчитаны по следующим формулам
.
При этом границы интервалов могут быть рассчитаны по следующим формулам ![]() ,
где N – количество временных шагов.
,
где N – количество временных шагов.
Разработанная математическая модель
была использована для компьютерного моделирования движения волны РЗ от
хранилища РАО к земной поверхности для изотопа - ![]() с постоянной
радиоактивного распада
с постоянной
радиоактивного распада ![]() год-1. При
этом следует отметить, что скорость адвекции очень мала и составляет согласно
[4]
год-1. При
этом следует отметить, что скорость адвекции очень мала и составляет согласно
[4] ![]() м/год, где квадратные скобки обозначают
границы интервала неопределенности. Примем, что скорость вытекания РЗ из
хранилища составляет примерно
м/год, где квадратные скобки обозначают
границы интервала неопределенности. Примем, что скорость вытекания РЗ из
хранилища составляет примерно ![]() 1/год.
Процесс распространения РЗ к земной поверхности аналогичен движению волнового
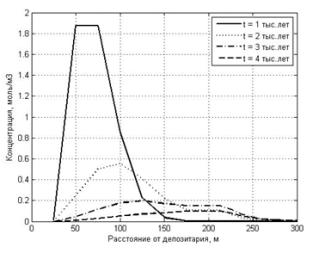
фронта. На рис.1 приведены результаты компьютерного моделирования. Суммарное
загрязнение, представленное на рис.1, является суммой загрязнений в первом (0 –
200м) и втором (200 – 300м) геологических слоях. Скорость подъема РЗ к
поверхности зависит в основном от скоростей адвекции в слоях и от скорости
вытекания РЗ из хранилища. Примем скорость адвекции в первом слое V1 =
0.05м/год, во втором слое V2
= 0.1м/год. При таких скоростях модельное время прохождения волнового фронта РЗ
для первого слоя составляет примерно 4 тыс. лет, а для второго слоя – одну
тысячу лет (см. рис.1а). Как следует из рис.1а, в начале максимум концентрации
расположен вблизи хранилища, а затем начинает равномерно распределяться по всей
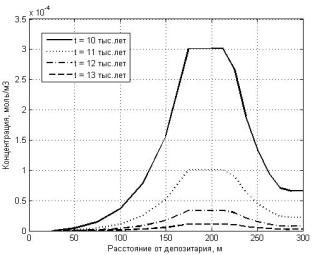
глубине геологического захоронения РАО. На рис.1б представлено распределение РЗ
для установившегося стационарного режима (формы графиков рис.1.б геометрически
подобны). При этом максимум распределения РЗ расположен на границе между
геологическими слоями. Это обусловлено более высокой скоростью адвекции РЗ во
втором геологическом слое, что приводит к быстрому оттоку РЗ от границы раздела
слоев. Постепенное уменьшение значения максимума обусловлено как переходом к
более равномерному распределению, так и вытеканием РЗ на земную поверхность.
Приблизительную оценку времени вытекания РЗ из хранилища можно получить
разделив начальную массу РАО (M0
~ 100 моль) на скорость вытекания (k ~ 0.01 год-1), что составляет около 10 тыс. лет.
1/год.
Процесс распространения РЗ к земной поверхности аналогичен движению волнового
фронта. На рис.1 приведены результаты компьютерного моделирования. Суммарное
загрязнение, представленное на рис.1, является суммой загрязнений в первом (0 –
200м) и втором (200 – 300м) геологических слоях. Скорость подъема РЗ к
поверхности зависит в основном от скоростей адвекции в слоях и от скорости
вытекания РЗ из хранилища. Примем скорость адвекции в первом слое V1 =
0.05м/год, во втором слое V2
= 0.1м/год. При таких скоростях модельное время прохождения волнового фронта РЗ
для первого слоя составляет примерно 4 тыс. лет, а для второго слоя – одну
тысячу лет (см. рис.1а). Как следует из рис.1а, в начале максимум концентрации
расположен вблизи хранилища, а затем начинает равномерно распределяться по всей
глубине геологического захоронения РАО. На рис.1б представлено распределение РЗ
для установившегося стационарного режима (формы графиков рис.1.б геометрически
подобны). При этом максимум распределения РЗ расположен на границе между
геологическими слоями. Это обусловлено более высокой скоростью адвекции РЗ во
втором геологическом слое, что приводит к быстрому оттоку РЗ от границы раздела
слоев. Постепенное уменьшение значения максимума обусловлено как переходом к
более равномерному распределению, так и вытеканием РЗ на земную поверхность.
Приблизительную оценку времени вытекания РЗ из хранилища можно получить
разделив начальную массу РАО (M0
~ 100 моль) на скорость вытекания (k ~ 0.01 год-1), что составляет около 10 тыс. лет.
а б
Рис.1. Движение волны радиоактивного загрязнения от хранилища к земной поверхности для радиоактивного изотопа I129: а – для периодов t = 1, 2, 3, 4 тыс. лет.; б - для периодов t = 10, 11, 12, 13 тыс. лет
Литература
1. Advanced Nuclear Fuel cycles and Radioactive Waste Management. NEA No. 5990. – London: OECD NEA, 2006. – 246p.
2. Бутусов О.Б., Мешалкин В.П., Попов Д.В., Тюкаев Д.А. Компьютерное моделирование радиоактивного загрязнения окружающей среды при разрушениях геологических хранилищ радиоактивных отходов с учетом неопределенности // Теоретические основы химической технологии. – 2013. – Т.47. - №6. – С.639 – 645.
3. Бутусов О.Б., Попов Д.В., Редикульцева Н.И. Компьютерное моделирование нечеткого уравнения переноса радиоактивных загрязнений // Известия МГТУ «МАМИ» - 2012. – т.4. – №2(14). – с.305-308.
4. Uncertainty in Industrial Practice: A guide
to Quantitative Uncertainty Management / Ed. by E. de Rocquigny, N. Devictor
and S. Tarantola. – New York: John Wiley & Sons, 2008. – 340p.