Кіф’як І.І, Жибчин Н.І

науковий керівник: к.ф.-м.н., доцент Дрінь Я.М.,

Буковинський державний фінансово-економічний університет,

м. Чернівці

«ЕКОНОМЕТРИЧНА МОДЕЛЬ ЗАЛЕЖНОСТІ ВАЛОВОГО ВНУТРІШНЬОГО ПРОДУКТУ ВІД ІНДЕКСІВ СІЛЬСЬКОГОСПОДАРСЬКОЇ ПРОДУКЦІЇ»

Досвід економічного моделювання показує, що використання економетричних моделей для прогнозування в економіці має вагоме місце. По-перше, проведення досліджень не потрібно використовувати великі кошти. По-друге проаналізовані дані, отримані за допомогою економетричних моделей, себе виправдовують. Останнім часом дослідження певних економічних явищ за допомогою економетричних моделей інтенсифікувались.

Для дослідження були використані статистичні дані за 2002-2012 роки. У таблиці 1 наведено дані про ВВП та індексів сільськогосподарської продукції за відповідні роки [3,4].

Таблиця 1.Співвідношення ВВП та індексів сільськогосподарської продукціїза 2002-2012 роки

( у % до попереднього року)

Роки	Валовий внутрішній продукт	Індекс продукції рослинництва	Індекс продукції тваринництва
2002	105,2	98,5	105,7
2003	109,6	85,9	93,9
2004	112,1	133,1	100,5
2005	102,7	97,5	105,1
2006	107,3	101,8	103,6
2007	107,9	90,9	98
2008	102,3	128,6	98,7
2009	85,2	95,3	104,2
2010	104,1	95,9	103,4
2011	105,2	130,4	101,3
2012	100,9	91,9	103,9

І. Специфікація моделі. Виберемо за незалежні змінні Х₁ – індекс продукції рослинництва, Х₂– індекс продукції тваринництва, за залежну змінну Y – ВВП. Розрахунки проведені за допомогою програми MS Exel, показали, що залежності між Х₁, Х₂та Y можна подати лінійною множинною моделлю з високим ступенем узгодженості R².

ІІ. Обчислення статистичної оцінки для вектора та побудова моделі. Оцінки параметрів лінійної економетричної моделі здійснювались за методом найменших квадратів з якого випливає формула оцінки параметрів лінійної регресії:

,

де - транспонована матриця до матриці[2].

Тож матриця на буде такого вигляду:

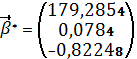
Отже, виходячи з [2], знайдені такі оцінкивектора {β₀, β₁,β₂}:

β₀ = 179,285, β₁ =0,078 , та β₂ = -0,822.

На основі цих даних побудуємо модель використовуючи формулу:

; ,

ІІІ. Аналіз ступеня адекватності побудованої моделі та вибіркових даних. Обчислимо вектор за формулою . Результати розрахунків наведені в таблиці 2. Правильність виконаних розрахунків можна перевірити, порівнюючи значення та , де

,

оскільки , попередні розрахунки правильні.

Визначимо ступінь адекватності моделі за статистичними даними, порівнюючи відхилення між фактичними значеннями та результатами обчислень за моделлю. Запишемо їх як елементи вектора [2].

Середнє значення , отже, розбіжностей не існує, а це означає що модель адекватна.

IV. Перевірка статистичної значущості коефіцієнта детермінації R²та критерію Фішера. Коефіцієнт детермінації R² = 0,2265 показує, що на 22,65 % варіація валового внутрішнього продукту пояснюється варіацією індексів сільськогосподарської продукціїпродукції.

Також дуже високий коефіцієнт кореляції вказує на тісну близьку до функціональної, залежність незалежних змінних Х₁ та Х₂ з залежною змінною Y.

Статистичну значущість моделі перевіряємо за допомогою F-критерію. Фактичне значення критерію порівнюємо з табличним значенням при ступенях вільності k₁ = 2, k₂ = 8і рівні значущості α = 0,05 . Оскільки гіпотеза про істотність зв’язку між залежною і незалежними змінними в даній економетричній моделі підтверджується, тобто лінійна форма зв’язку в моделі вибрана правильно.

V. Визначення дисперсій оцінок та їх стандартних помилок. Знайдемо тепер незміщену оцінку для дисперсії залишків за формулою:

де n = 11, m = 2.

Отже, незміщена оцінка для дисперсії залишків = 47,703. Далі ми знаходимо коваріаційну матрицю оцінок параметрів для виявлення дисперсій, яка визначається за формулою:

.

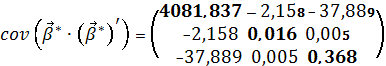
Визначивши матрицю ми знаходимо дисперсії оцінок параметрів, де вони дорівнюють добуткам діагональних елементівc_ijматриці [2]. Отже, дисперсії оцінок параметрів такі:

4081,837; 0,016;0,368.

Середньоквадратичні відхилення оцінок параметрів такі:

63,889; 0,126; 0,606.

Перевіримо статистичну значущість параметрів β₀, β₁та β_2. Для цього ми скористаємось критерієм Стьюдента, де спостережувані значення статистичних критеріїв дорівнюють:

.

Для побудови двобічної критичної області при α = 0,05, k = n – m – 1 = =11 – 2 – 1 = 8 знаходимо (α/2,k) = (0,025;13) = 2,306. Оскільки, , то відкидаємо гіпотезу про присутність мультиколінеарності.

VI. Розрахунок довірчих інтервалів для оцінок параметрів β₀, β₁та β₂. Довірчі інтервали оцінок параметрів такі:

31,957<<326,614 ;

-0,212<<0,369;

-2,221<<0,576 .

На основі побудованої регресії можна зробити висновок, що ВВП, який залежить від індексівсільськогосподарської продукції, рівних середнім значенням = 104,53 % та = 101,66 %, дорівнювала би при β₀ = – середньому значенню залежної змінної = 103,864. Збільшення індексупродукції рослинництва(на 0,08 %) та зменшеннятваринництва (0,82 %)за один рік призводить до збільшення ВВП. Фактори, включені в модель пояснюють «поведінку» ВВП на 22,65%.

VII. Розрахунок прогнозного значення та побудова для нього довірчих інтервалів. Оскільки значення ВВП залежить від індексів сільськогосподарськоїпродукції, доцільно розрахувати точковий прогноз та довірчі інтервали прогнозу. Для цього задамо вектор прогнозних значень незалежних змінних x_p =96,95 – індекспродукції рослинництва та 111,74 – індекс продукції тваринництва[1]. Ці дані ми взяли з прогнозів індексів сільськогосподарської продукції на 2014 рік. Тож, прогнозне значення ВВП дорівнює

;

тобто прогнозний ВВП на 2014 рік становить 98,94%.

Далі ми знаходимо можливе відхилення s_p:

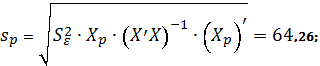
де – матриця прогнозних значень, - транспонована матриця до матриці . Отже, похибка ВВП дорівнює 64,26 %.

Обчислюємо нижню та верхню межу прогнозного значення :

-53,21<<243,17

Отже, потенційний ВВП на 2014 рік може коливатися приблизно від -53,21 % до 243,17 %.

VIII. Визначення часткових коефіцієнтів еластичності. Ми визначаємо коефіцієнти еластичності за такою формулою:

;

Коефіцієнти еластичності до β₁та β₂ дорівнюють:

0,001;-0,004

0,001 інформує про те , що при збільшенні індексупродукції рослинництва на k відсотків значення залежної змінної Y (ВВП) збільшиться на 0,1kвідсотків, а при зменшеннііндексу продукції тваринництва на k відсотків значення залежної змінної Y збільшиться на 0,4kвідсотків.

Отже, на основі отриманого економетричного рівняння можна стверджувати про наявність між ВВП та індексами сільськогосподарськоїпродукції лінійної форми зв’язку. Встановлено, що великий вплив на ВВП має індекс продукції тваринництва.

Використання економетричного моделювання дозволяє визначити ефективність впливу на ВВП індексів сільськогосподарської продукції. За допомогою отриманих моделей можна робити прогноз щодо ВВП на майбутні періоди.

Список використаної літератури

1. Україна: Перспективи розвитку – консенсус-прогноз: Міністерство економічного розвитку і торгівлі України, 2013. – 35 с.

2. Економетрія: Навч. Посіб. / В.І. Жлуктенко, Н.К. Водзянова, С.С. Савіна, О.В. Колодінська; За загальною редакцією кандидата економічних наук С.І. Наконечного. – К.: Видавництво Європ. ун-ту, 2005. – 552 с.

3. Статистичний щорічник України за 2011 рік. – К.: Техніка,2012. – 558 с.

4. Валовий внутрішній продукт за 1996-2011 рр.: [Електронний ресурс] : Державний комітет статистики України. — Режим доступу: http://www.ukrstat.gov.ua.