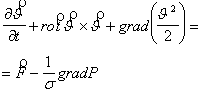Исаева Д.А.,
Бабылханова Г.Н., Ташенова А.
Таразский
государственный университет имени М.Х. Дулати. Казахстан
Энергетическая интерпретация уравнений
движения вязкой жидкости в форме Абдураманова
Этапы развития гидродинамики условно
можно увязать с динамикой составления основных дифференциальных уравнений
движения потока жидкости (см. таблицу).
Таблица
Динамика
составления основных дифференциальных уравнений движения потока жидкости
|
Наименование дифференциальных уравнений движения твердых тел и
жидкости |
Структура дифференциальных уравнений |
|
Дифференциальное уравнение Ньютона для движения твердых тел [1] |
|
|
Дифференциальное уравнение Эйлера для движения идеальной жидкости [2] |
|
|
Дифференциальное уравнение движения идеальной жидкости в форме Громеки [3] |
|
|
Дифференциальное уравнение движения идеальной жидкости в форме Ламба-Громеки [4] |
|
|
Дифференциальное уравнение движения реальной жидкости в форме Навье-Стокса[5,6] |
|
|
Дифференциальное уравнение движения реальной жидкости в форме Абдураманова [7] |
|
При этом
приняты следующие обозначения:
![]() - скорость потока жидкости;
- скорость потока жидкости; ![]() - массовая сила;
- массовая сила; ![]() ;
; ![]() - плотность жидкости; Р- давление; u-потенциал силы, Е-удельная
энергия,
- плотность жидкости; Р- давление; u-потенциал силы, Е-удельная
энергия, ![]() ; ν-коэффициент кинаматической вязкости;
Δ-лапласиан,
; ν-коэффициент кинаматической вязкости;
Δ-лапласиан, ![]() ; t- время;
; t- время; ![]() - вектор «вторых вихрей»,
- вектор «вторых вихрей», ![]() .
.
Из уравнений
(6) видно, что вихрь от вихря (![]() ) так же как вязкость, уменьшает массовую силу, сообщающую
частицам жидкости соответствующие ускорения.Вихрь от вихря так же уменьшает
скорость движения потока жидкости.
) так же как вязкость, уменьшает массовую силу, сообщающую
частицам жидкости соответствующие ускорения.Вихрь от вихря так же уменьшает
скорость движения потока жидкости.
Не менее
интересную структуру получают дифференциальные уравнения движения жидкости,
представленные в форме Ламба-Громеки, если учесть влияние вязкости, ![]() , то есть
, то есть
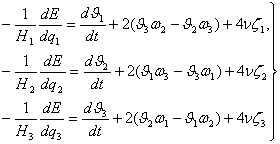 (7)
(7)
где Н1, Н2,
Н3- - коэффициенты Лямэ; q1, q2, q3-
криволинейные координаты, ![]()
![]()
![]() - компоненты вектора скорости;
- компоненты вектора скорости; ![]()
![]()
![]() - компоненты вектора угловой скорости вращения частиц;
- компоненты вектора угловой скорости вращения частиц; ![]()
![]()
![]() - компоненты вектора «вторых вихрей».
- компоненты вектора «вторых вихрей».
Уравнение (7) в вектором виде представляется короче
![]() , (8)
, (8)
где Е – запас энергии потока
жидкости, ![]() ;
;
u –
потенциал силы.
Таким образом, удельная энергия потока жидкости уменьшается тем больше, чем
больше степень не стационарности течения, вихреобразования и преобразования
первичных вихрей на «вторых вихрей».
Для стационарных потоков эти уравнения
имеют вид:
![]() (9)
(9)
то
есть запас энергии расходуется на образования «первых и вторых вихрей».
В случае когда имеет место винтовое движение, то
![]() (10)
(10)
или
![]()
Следовательно уравнение (9) имеет следующий вид:
![]() (11)
(11)
или
![]() (12)
(12)
то есть запас энергии расходуется на преодоление сопротивления,
возникающих «вторыми вихрями» и вязкостью
жидкости.
ЛИТЕРАТУРА
- Ньютон И. Математические начала натуральной философии. Перевод на русский язык акад. А.Н. Крылова М., 1987. -701с.
- Эйлер Л. Общие законы движения жидкостей. Механика жидкости и газа №6, 1999, с.26…54. Перевод З.Н. Добровольской с французского мемуара Л.Эйлера.
- Громека И.С. Некоторые случаи движения несжимаемой жидкости. М.: АН СССР, 1952. –с.76….132.
- Ламб Г. Гидродинамика. –М-Л.: ОГИЗ, 1947. -928с.
- Чугаев Р.Р. Развитие и формирование технической механики жидкости (гидравлики) –Л.: 1975, с..25.
- Штеренлихт Д.В. Гидравлика – М., 1984, 639с.
- Абдураманов А. Механика вихревых и винтовых потоков жидкости и ее приложение в гидротехнике, ч.1, Ташкент, 1982. -81с.