Математика/2. Перспективы информационных систем
Магистрант Онгарбаев С.К.
Западно-Казахстанский
государственный университет имени Махамбета Утемисова, Казахстан
МАТЕМАТИКА САБАҒЫНА ОҚУШЫЛАРДЫҢ
ҚЫЗЫҒУШЫЛЫҒЫН АРТТЫРУДА ЭЛЕКТРОНДЫҚ РЕСУРСТАРДЫ
ПАЙДАЛАНУ
Үздіксіз білім беру
жүйесінде математиканы оқытудың мақсаттарын іс
жүзіне асыру үрдісі дидактиканың қағидаларын,
мазмұнын, оқыту формалары мен құралдарын зерттей келе, білім алушыларға қазіргі заман
мектеп математика бағдарламасының негізгі рухани
мазмұндық-әдістемелік бағыттары жөнінде білім
бере отырып, қазіргі замандағы білім беру әдістерін
және қазіргі мәдени-әлеуметтік кезеңнің
ерекшеліктерін ескере отырып, математиканы оқытудың жаңа әдістемелерін,
ақпараттық технологияларды пайдалануды, креативтік
әдістемелер мен интерактивтік тәсілдерді қолдануды,
математикадан үздіксіз білім берудің ұлттық жүйесін дамытудың
ғылыми-әдіснамалық негізін ескеруді, әлемдік білім беру
кеңістігінің ерекше өлшем бірлігі ретінде математикадан
үздіксіз білім берудің қазақстандық
жүйесінің мәдени-мазмұндық,
рухани-қазыналық, әлеуметтік-этникалық ерекшеліктерін
зерттеуді талап етіп отыр.
Зерттеу жұмысы осы
кездегі мәдени-әлеуметтік кезең мен қазіргі
заманғы математиканы оқыту әдістемелерін ескере отырып,
математикадан Қазақстандағы ұлттық үздіксіз
білім беру жүйесін дамытудың ғылыми-әдістемелік
негіздерінің бірі ретінде Қазақстандағы 12 жылдық үздіксіз білім беру жүйесіне өту
жағдайында мектеп математикасын оқытуда компьютерлік анимацияларды
пайдалану әдістемесін жасау, сипаттама беру және математиканы
оқыту әдістемесіне енгізу; сол арқылы жеке
тұлғаны дамыту бойынша халықаралық бағдарламаны,
сонымен бірге Қазақстан Республикасының Ұлттық
үздіксіз білім беру жүйесін модернизациялаудың мемелекеттік
бағдарламасын қолдау және қолданысқа енгізу болып
табылады. Ал, соңғы
нәтиже ретінде: оқу материалын сапалы игеру және білім
алушылардың жеке-тұлғасын дамыту көзделініп отыр.
Оқушыларды математика
сабағына қызықтыру негізінде олардың логикалық
ойлау үрдісін өздерінде қалыптастыру арқылы
базалық бағдарламаны игеруі мен өзіндік дамуға
бағыттау математикадан білім берудің негізі болып табылады. Бұл
өз кезегінде жаңа ақпарат технологиялары мен
әдістемелік құрылымдарға сүйенеді:
математикалық ойлауды қалыптастыру, математикалық білім
алуға логикалық бағытты қалыптастыру, дарынды
оқушыларға терең білім беруді қамтамасыз ету,
математикалық дүние танымды қалыптастыру, математиканы
ұнатпайтын оқушыларды математикаға қызықтыру, оларға
білім беруде математиканы оқытудың
психологиялық-педагогикалық аспектілерін ескеру т.б..
Осындай жаңа технологиялық әдістемелердің
бірі оқытуда компьютерлік анимацияларды пайдалану. Компьютерлік анимация
техникаларының комбинациялары әртүрлі болады (расторлық
анимация, векторлық графика т.б). Ал нағыз анимацияны жасау
үшін Flash-технологиясы қажет деп есептейміз.
Flash – ағылшын тілінен
аударғанда «найзағай», «жарқ ету» дегенді білдіреді.
Бұл атау осы технологияның өзінің мәнін
және оның даму қарқынын көрсетеді [1].
Математиканы оқыту дидактикасына қатысты идеяларды
іске асыру үшін CD-де әртүрлі мультимедиялық жобалар
мен телевизиялық графиктер үшін анимациялар жасауда осы технологияны
пайдалану жеткілікті бола алады. Оқыту бағдарламалары үшін
жасалатын әртүрлі үрдістерді көрсету үшін, ойын
элементтерін оқытуда пайдалану үшін, математикалық
тәуелділіктердің графиктерін, диаграммаларды, олардың
қозғалысын көрсету үшін бұл таптырмайтын
әдіс. Дайын материалдардан гөрі әрбір оқытушы
өзінің жеке анимациясын қарапайым болса да жасағаны
дұрыс. Бұл біреудің жұмысын рұқсатсыз
пайдаланудан да сақтайды.
Бағдарламалық
анимация құрастырылатын элементар нысандар өте
қарапайым бола алады (шеңберлер, кесінділер, нүктелер,
үшбұрыштар т.б.) немесе өздері анимациясы бар клиптер де бола
алады.
Flash-технологиясы математикалық есептеулер жүргізуге
бағытталмаған, сондықтан мұнда күрделі
математикалық есептеулер жүргізу қажет емес [1. – 332-333 бб.].
Біздің мақсатымыз
Flash-технологиясын үйрету емес, математиканы оқытуда оның
мүмкіндіктерін пайдаланатын әдістемелік идеялар жөнінде айту
болып табылады. Ал, математиканың кез-келген тақырыптарының
бірін оқытудың жақсы әдісінің идеясын берсе,
оның анимациясын жасауды орта қол кез-келген компьтердің
маманы іске асырып бере алады.
Біз көркем сурет
туындыларын тамашалағанда, әсіресе тіршілік, қозғалыс
белгісі бар, тірі табиғат бейнеленген суреттерге назар аударамыз.
Қозғалыс элементі сезілмейтін ешнәрсе адам баласын қызықтырмайды. Қозғалыстағы
әрекеттер бейнеленген қызықты әдістемелер
деңгейлік және табиғи бейімділіктер бойынша саралап
оқытуды ескере отырып жасалуы тиіс, нысанды қызықты
тапсырмалар жүйесін және компьютерлік технологияларды математиканы
оқытуда қолданатын әдістемелер жасалғанда және
тәжірибеде қолданысқа енгізгенде баланың инстинкті
табиғи бейімділіктерін ескерумен қатар, үлкен де, кіші де
адамдарды кәдімгі қозғалыстың
қызықтыратынын ескеріп, математиканы оқытуды
«қозғалту» қажет деп есептейміз. Бұны іске асыруда біз
құралдарды [2], өмірде пайдаланатын, күнделікті қолданатын заттарды [3] және компьютерлік анимацияларды [4]
пайдаланғанымыз жөн.
Белгілі американдық
психолог Э.Торндайк: «Заттардың қозғалуы – баланың
заттарға назар аударуы мен физикалық қозғалысқа
рахаттанып қарауының инстинктивті бейімділігі... Мысалы, бөлшектер
алма мен пышақтың көмегімен оңай игеріледі», – деп жазған [4. – 18-19 бб. ].
Математиканы оқытуда
компьютерлік анимацияның көмегімен элементтердің көбін
қозғалтуға болады. Мысалы: бөлшектердің алымдары
мен бөлімдерін, олардың бүтін бөліктерін, толықтауыш
көбейткіштерін, ортақ бөлімдерін, квадрат
теңдеулердің графиктері арқылы түбірлерінің бар
жоғын білу, дискриминанттың теріс, оң, ноль болу шарттарын;
теңдеулер құру, матрицаларға амалдар қолдануда
элементтерді орынан жылжыту, теңсіздіктердің шешімдерінің
суреттерін қиылыстыру, теоремалар мен олардың
дәлеледемелерін, суреттері мен графиктерін жылжыту арқылы
дәлелдеуді көрнекілендіру, планиметриялық және стереометриялық есептер
құру мен шығаруда белгісіздер мен есептің шартын
түсіну, салу есептерінің шығарылу жолын көрсету т.б.
Күрделілігі жоғары геометриялық есептерді
шығарғанда дайын сызбаларды пайдаланудан гөрі, сызу
үрдісін біртіндеп, логикалық үрдісте сызып отыру,
түсінуге оңай екені белгілі. Міне, осы үрдісті компьютерлік
анимация логикалық жүйе бойынша сыза отырып, есепті тез
түсінуге, эстетикалық жағымды әсер алуға септігін
тигізеді.
1-Мысал. Үш белгісізі
бар үш сызықтық теңдеулер жүйесін
құрастыру.
Айталық,
құрастырылмақ сызықтық теңдеулер
жүйесінің шешімі 
болсын, яғни 
. Құрастырылатын сызықтық
теңдеудің коэффициенттері мен олардың таңбаларын
қалауымызша алып, теңдеулер жүйесін
құрастырайық:
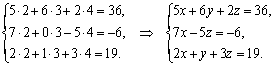
Есепті
құрастырудың компьютерлік анимациясын жасағанда
коэффициенттерді белгілі ретпен қозғалтып, оқушының
назарын қажетті бағытқа қызықтырып
бағыттауға болады.
2-Мысал. Берілген үш
белгісізі бар үш сызықтық теңдеулер жүйесін
Крамер әдісін пайдаланып шешу
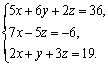
Есепті шешу үрдісіндегі
анықтауыштарды есептеу ережесін оңай игеру үшін компьютерлік
анимациясының көмегімен, көбейтіліп қосылатын сандарды
біркелкі түспен ерекшелендіріп, жылжытып әкеп қосып, білім
алушының ережені еркін меңгеруіне жағдай жасауға
болады.
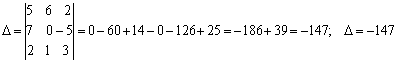
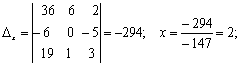
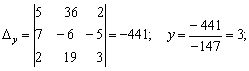
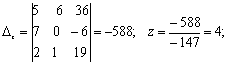
Жауабы: 
.
3-Мысал.
Жазықтықтағы екі түзудің параллельдік
белгісінің (оларды үшінші түзумен қиғандағы
пайда болған ішкі айқыш бұрыштардың теңдігі
бойынша) компьютерлік анимациясын жасауды сызықтарды
қозғалысқа келтіріп, тең бұрыштарды
анимацияның көмегімен жалтырату арқылы оқушының
назарын аудару қажет.
4-Мысал. Фаллес теоремасы
бойынша берілген кесіндіні төрт теңдей бөліктерге бөлу
үрдісінің компьютерлік анимациясын жасасаңыз,
кесіндінің ұшынын жүргізілетін түзудің
анимациясын көрсетіп, пайда болған бұрыштың
қабырғаларына салынатын кесінділердің теңдігіне,
соңғы кесіндінің соңғы ұшы мен
бөлінуге тиіс кесіндінің соңғы үштарын
анимацияның көмегімен қосып, қосу сызығына
жүргізілген параллель түзулерді ерекше жарқыратып,
оқушының назарын аудару қажет.
5-Мысал. Ені кеңдеу, ал ұзындығы
қысқалау тақтайдан үш рет кесіп, бір рет желімдеу
арқылы ұзындығы ұзынырақ, ал ені тарлау
сөре жасаудың әдісін ойлап табыңыз (стандарт емес
ойлау).
Берілген тақтайды 
деп белгілейік.
Есептің шартын орындау үшін тақтайды 
диагоналінің
бойымен қиып, пайда болған екі үлкен тікбұрышты
үшбұрыштарды сол диагональ бойымен қарама-қарсы
бағытта анимацияның көмегімен жылжытып, ортасын диагональ
бойымен желімдеу кажет. Осы үрдісте пайда болған артық екі
фигураны (шеткі екі кіші тікбұрышты үшбұрышты) тағы да
анимацияның көмегімен қиып тастасақ, есептің
шартына сай келетін сөре дайын болады.
Есепті шығару
үрдісінің компьютерлік анимациясы стандартық емес ойлауға анимацияның
көмегімен оқушының назарын аударады.
6-Мысал. Пифагор теоремасының А.Эйнштейннің дәлелдемесі
мен орта ғасырлық шығыс ғалымы әль-Нәзір
дәлелдемесінің [5] компьютерлік анимациясын жасағанда Пифагор фигурасындағы
негізгі тік бұрышты үшбұрышты, оның
қабырғасына саланған шаршыларды әртүрлі
түске бояп, жүргізілетін сызықтарға
оқушының назарын аудары қажет. Бұл анимация катеттерге
салынған шаршыларды гипотерузаға салынған шаршыға
жылжытып әкеліп, толық қамту арқылы оқышыны
Пифагор теоремасының геометриялық мағынасын түсінуіне
үлкен септігін тигізеді.
Математикадан білім берудің негізі
қызықты математикадан, дидактикалық ойындардан, компьютерлік
технологиялардан құралуы тиіс, бұның қорытындысы
теориялық білімдерді, математикалық заңдылықтарды
практикада сауатты қолдануға әкелмек.
Біз математиканы оқыту
үрдісінде баланы қызықтыратын, логикалық ойлауды
белсенділендіретін, математиканы «құрғақ пән»,
«табиғат пен өмірден алшақ пән» деген ұғымдардан,
көзсіз «академиялылыққа» ұмтылудан арылтып,
табиғатты танып білуге, оны қорғауға құштар
ұрпақ өсіруге септігін тигізетін оқыту технологияларын
тынбай іздестіруге бағыт ұстау қажет деген ойдамыз.
Математикадан білім беруде
математиканы оқытудың біз «қызықты әдістемесі»
деп атаған әдістемеміз, соңғы компьютерлік
технологияларды сабақ үрдісінде пайдалана отырып, білім
алушылардың математикалық, логикалық және оңтайлы
ойлауын оятып, математика пәніне қызығушылыққа
жетелейтін ғылыми мақсаты бар жаңа әдістеме.
Әдебиеттер
1.Черкасский В.Т. Эффективная анимация во Flash. – М.: Кудиц-образ, 2002. – С.: 4-332.
2. 9. Gitlow H., Gitlow S., Oppelheim A.,
Oppelheim R. Tools and methods for the improvement of quality. – Boston, 1989.
– 603 p.
3 Торндайк Э. Л. Бихевиоризм
(инстинкты и способности). //
[Электрондық ресурс]. – 2012. –
Сайттағы жету режимі: http://ethologi.
ru /library?/id =149.
4. Джанабердиева С.А. Образовательные технологии гуманитаризации преподавания для учащихся не успевающих по математике в общеобразовательной школе. / Материалы III международной научно-практической конференции «ИТОЭУ». – Воронеж, 2006. – С. 142-148.
5. Генкин Г.З. Этюд об аркусах. //М: Математика в школе, 2005. – № 5. – 47 с.
6. Теорема Пифагора / Коллекция доказательств - [Электрондық ресурс]. – 2012. – Сайттағы жету режимі: http://tambov.fio.ru/vjpusk/vjp016/rabot/15dokasatelstwo.htm
7. Теорема Пифагора // [Электрондық ресурс]. – 2012. – Сайттағы жету режимі:
http://www.cut-the-knot.com/pythagoras/