Mathematics / 4. Applied Mathematics /

O.F. Ryaboshtan, Ph.D. A.M. Milenin, Ph.D. S.M. Skofenko

Kharkov National Technical University of Agriculture after P. Vasilenko

Construction of two-dimensional linear frame bypass gas turbine blade

Analytical description of two-dimensional contours using interpolation formulas is not always easy due to the fact that does not involve getting certain lines on the surface.The problem of obtaining a linear frame bypass gas turbine blade is fundamental to the design of the fairings, and connect various transitional surfaces while filling the space curvilinear quadrangle (portions of space).

Suppose that the order of band II

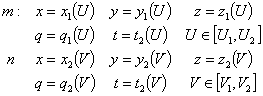
The remaining partial derivatives , bands are calculated from the known relations:

,

, (3)

The task is to build on the edges of the frame cover and satisfying the specified equipment. Obviously, it is not the only solution, both in terms of application, and uncertainty in the choice of "transverse" tangents and second derivatives on the edges bypass portions of space (they are the first and second derivatives of the frame lines).

Let us consider the following scheme design. For each of the projections and apply the formula bypass flat second-order smoothness, for example

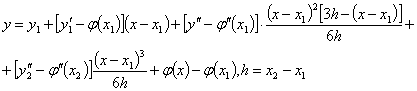(4)

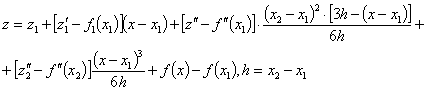(5)

In order to apply Equation (4) and (5) if, using the specified , , , , on the edges bypass portions interscapulum, somehow determine , , , . This choice is not unique and is carried out with the help of equations

, (6)

. (7)

It is best to set the value (of the set of admissible) and plane and determine according to the formulas and .

Suppose such a choice is made and functions , , , defined on the edges.

To fill the entire compartment establish between and conformity

(8)

Before calculating the bypass function is desirable, given band by means (8) expressed in terms of (let it be) , , … , . Then equation (4) and (5) would have a single parameter .

Function two-parameter

. (9)

Options and determined by solving a system of equations with , , , .

Thus, the input feature for (5) and defines its parameters.

After determining the functions and written by equations (4) and (5), the joint consideration of which gives the desired equation compartment consisting of line .

When considering compartment conjugating two surfaces, each of which is assigned a coupling line, and calculated the transverse tangent function and the second derivatives along the connecting line. Normally, parametric line interface and their derivatives can be assigned as , , , . Naturally, the functions are consistent with the functions of the normal curvature of the surface and along the connecting line. With this organization, a method for designing gas turbine blades pairing occurs on the second order parametric smooth both surfaces of the lines, which makes it possible to organize the whole surface of the through parameterization. This is convenient for solving a complex engineering problems.