А.И. Долгарев

ИСПРАВЛЕНИЕ НЕТОЧНОСТЕЙ В РАБОТАХ О ПОВЕРХНОСТЯХ

В работах [1 – 3] в формулах и формулировках некоторых утверждений по вине автора допущены неточности. В связи с этим приношу читателям свои извинения. Как это ни досадно, но неточности влекут негативное отношение к работам и автору. Если бы неточности в тексте не влияли на восприятие содержания, то о неточностях можно было бы не заботиться. Вместе с тем, осуждаемые огрехи относятся к математическим текстам. Во многих случаях неточности в текстах автора могут быть устранены на основе других фрагментов текстов в результате внимательного прочтения текста, при условии, что читатель понимает детали и основную линию работы, выстраеваемую автором.

Сначала приведу неточности, допущенные мною, укажу, как они устраняются, какими правильными формулами и формулировками они устраняются, точнее: какими правильными формулами и формулировками они должны быть заменены. После этого проанализирую свои тексты на предмет устранения допущенных опечаток.

1. Коэффициенты формы кривизны поверхности

Рассматриваются далее регулярные поверхности 3-мерного евклидова пространства. В [1] впервые получены формулы, выражающие коэффициенты формы кривизны (второй квадратичной формы) поверхности = через коэффициенты ее метрической формы (первой квадратичной формы). Имеем известные формулы:

, , , ; , , .

Находим: , . Перемножаем равенства с учетом , получаем 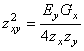. Выполняется

1. УТВЕРЖДЕНИЕ. Справедливо неравенство

. (1)

# В левой части равенства перед утверждением записана неотрицательная величина , следовательно, (1) выполняется. #

Это очень важный факт, он нигде не отмечен ввиду его очевидности. Из утверждения 1 получается

2. СЛЕДСТВИЕ. Знаки величин и одинаковы. #

Поэтому имеет смысл формула

= .

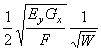Заметим, что в формуле для в [1, c. 56] допущена опечатка: вместо напечатано . В обзоре [2] факт (1) не отмечен, а указанная опечатка исправлена. Утверждение 1 и его следствие 2 должны быть выделены; они используются в установлении значимых фактов.

2. Формулы кривизны

Выражения коэффициентов формы кривизны поверхности через коэффициенты метрической формы позволили выявить новые возможности метрической формы поверхности. В частности, в [3] рассматриваются формулы для средней кривизны поверхности и нормальной кривизны линий на поверхности. Средняя кривизна поверхности ошибочно записана в виде:

.

Правильное значение средней кривизны поверхности таково:

.

Здесь используется следствие 2. Так как знаки величин и одинаковы, то подкоренное выражение неотрицательно. Нормальная кривизна линий на поверхности в направлении в [3] ошибочно записана в виде:

,

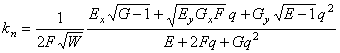правильная формула такова:

.

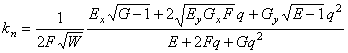И здесь использовано следствие 2. Указанные формулы в ошибочном виде переписаны в обзоре [2] и в [4].

3. О формуле Гаусса

В работе [1] ошибочно утверждается, что в книге [5] формула Гаусса неверна. В подтверждение приведен пример с поверхностью = .

Вычислены производные 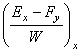, 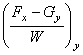вместо 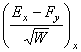, , 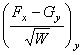содержащихся в рассматриваемой формуле Гаусса

.

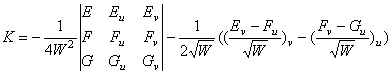Вывод, сделанный в [1], неверен.

4. Об основной теореме теории поверхностей

По недоразумению в обзоре [2] дана не та формулировка основной теоремы теории поверхностей. Содержание основной теоремы теории поверхностей состоит в том, что в ней указываются условия определяемости поверхности. В середине XIX века было установлено, что регулярная поверхность 3-мерного евклидова пространства однозначно, с точностью до положения, определяется заданием коэффициентов первой и второй основных квадратичных форм и при этом должны выполняться формулы Гаусса – Петерсона – Кодацци. После получения в [1] выражений коэффициентов второй квадратичной формы поверхности через коэффициенты первой квадратичной формы

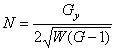, , (2)

(формулы из [2]) содержание основной теоремы теории поверхностей претерпело изменения. Теперь это содержание таково.

3. ОСНОВНАЯ ТЕОРЕМА. [3, теорема 5] Регулярная евклидова поверхность коэффициентами метрической формы (первой основной квадратичной формы) поверхности определяется однозначно, с точностью до положения в пространстве. #

В выводе формул (2) не использованы формулы Гаусса – Петерсона – Кодацци, поэтому они не упоминаются в формулировке основной теоремы. Формулировка теоремы 3 ассоциируется с результатами по теории евклидовых поверхностей, приведенными в обзоре [6]. В работах, цитируемых в [6], установлено, что поверхность евклидова пространства определяется коэффициентами метрической формы (первой основной квадратичной) при условии наличия формул Гаусса – Петерсона – Кодацци. Для поверхностей 3-мерного пространства последнее условие в [1] снято.

В работе [4], опубликованной одновременно с [2], дана верная формулировка основной теоремы, а в [2] по необъяснимым причинам приведена формулировка, не соответствующая содержанию основной теоремы; в ссылке на первоисточник ошибочно указана работа [1] вместо работы [3].

5. Комментарии к неточностям

Смысл рассматриваемого вопроса иногда позволяет установить правильность приводимого в тексте работы результата. Понятно, что рискованно использовать всякий результат без обоснования. Если уж есть обоснование результата, то в обоснование нужно скрупулезно вникать. Это всегда полезно, но не всегда способствует достижению цели.

Указанная в п. 1 опечатка в [1] исправима по смыслу текста. В тексте не рассматриваются функции и их производные. Всюду речь идет о производных функции . Проверка по полученному значению производной подтверждает, что должен быть записан квадрат производной .

Формулы для средней кривизны поверхности и нормальной кривизны линий на поверхности в [1] в тексте работы призывается получить на основе полученных выше формул (2). Приведенные формулы не являются распространенными, поэтому нуждаются в проверке.

Объявленная в [1] неправильность формулы Гаусса из [5] ниже по тексту работы [1] обосновывается. Неправильность известной формулы вызывает сомнения, поэтому предложенное обоснование требует того, чтобы в него вникнуть. В п.3 найдена и указана ошибка в обосновании. Это заметит и внимательный читатель.

Утверждение 1 и следствие 2 из него могут быть выделены при внимательном чтении текста работы [1]. Невыделение в тексте работы указанных утверждений является упущением автора.

Подмена в [2] смысла основной теоремы теории поверхностей недопустима. В других работах автора этого нет, но все-таки, подмена недопустима.

Приведенные комментарии не снимают с автора ответственности за допущенные неточности, ошибки и опечатки. Здесь содержится призыв к внимательному отношению к текстам во избежание получения неверных сведений.

Список литературы

1. Долгарев А.И. Новый вид основной теоремы Гаусса в евклидовой теории поверхно-

стей.// Materiali IX mezinarodni vedecko-praktika conference «Dni vediy – 2013» - Dil

32. Matematika. Vystavba a archtektura: Praga. Publiching House “Education and

Skience”. s.r.o. – 2013. С. 55 – 60.

2. Долгарев И.А. и Долгарев А.И. Определяемость евклидовой поверхности. Обнов-

ленная основная теорема теории поверхностей (обзор теории поверхностей).// Mate-

rialy IX Miedzynarodowej naukowi-praktycznej konferencji “Perspektywiczne opra-

cowania sa nauka I technikami – 2013” Volume 33. Matematyka.: Przemysl. Nauka i

studia – 2013, C. 27 – 47.

3. Долгарев А.И. Добавочные возможности первой квадратичной формы евклидовой поверхности. // Materialy IX Miedzynarodowej naukowi-praktycznej konferencji “Dinamika naukowych badan – 2013” Volume 12. Matematyka. Fizyka. Nowoczesne informacyjne technologie. Chemia I chemiczne technologie: Przemysl. Nauka i studia – 2013, C. 20 – 26.
4. Долгарев И.А., Долгарев А.И. Обновленная основная теорема теории поверхностей в курсе геометрии. // Информационные технологии в математике и математическом образовании. Материалы II Всероссийской научно-методической конференции. Красноярск: КГПУ – 2013, С. 327 – 331.

5. Позняк Э.Г., Шикин Е.В. Дифференциальная геометрия. – М.: Изд-во МГУ, 1990. – 384с.

6. I. Ivanova-Karatopraklieva, P.E. Markov, I. Kh. Sabitov. Bending of surfaces. III. Fundamentalnaya i prikladnaya matematika, vol 12. (2006), no 1, pp. 3 – 56.