Математика / 5. Математическое моделирование

Пирогова А. В.

Одесский национальный морской университет, Украина

Идентификация обыкновенных дифференциальных уравнений

При исследовании переходных процессов в детерминированных динамических системах с сосредоточенными параметрами используются математические модели в виде обыкновенных дифференциальных уравнений (ОДУ). Эти модели можно установить путем параметрической идентификации элементов действующих систем на базе экспериментальных данных [1].

Как правило, экспериментальные зависимости Xе(τ) (воздействие на объект) и Yе(τ) (реакция объекта) обычно зашумлены.

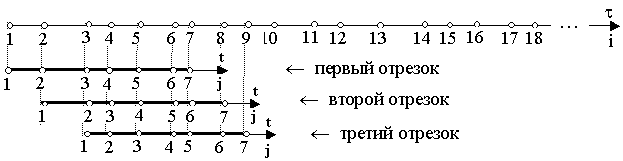
Вся область изменения величин Xe(τ) и Ye(τ) разбивается на отрезки времени Dt, перекрывающие друг друга. Используется метод скользящих отрезков (Рис.1). На каждом выделенном отрезке используется локальная в пределах каждого отрезка независимая переменная t.

Рис. 1. Схема разбиения области отрезки при идентификации

Для решения задачи идентификации используется метод наименьших квадратов при котором:

¾ проводится аппроксимация зависимостей Xе(t) и Yе(t) на отрезках оси времени гладкими функциями (полиномы невысоких степеней) и определяются производные , , ;

¾значения функций и производных подставляются в идентифицируемое уравнение и определяется сумма квадратов невязок левой и правой частей уравнения d для всех рассматриваемых моментов времени;

¾значения коэффициентов идентифицируемого дифференциального уравнения определяются путем минимизации суммы квадратов невязок левой и правой частей уравнения.

Качество идентификации уравнений существенно зависит от удачного выбора количество моментов времени на отрезке аппроксимации Jm и порядка аппроксимирующего полинома Kpol.

Важным является оценка достоверности результатов идентификации. Поэтому предварительно осуществляется сглаживание [2] зашумленных экспериментальных зависимостей Xе(τ) ® Xs(τ) и Yе(τ) ® Ys(τ).

Качество результатов идентификации математической модели объекта оценивается сравнением значений Ys(τ) и восстановленных значений Ych(τ) полученных путем решения идентифицированного уравнения надежным численным методом. При этом в качестве воздействия рассматривается Xs(τ).

В качестве оценки используется среднеквадратичное отосительное рассогласование Ych(t) и Ysm(t) (Sigmsm).

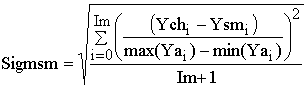, (1)

где Im – количество записей в выборке (количество моментов времени).

Для оценки влияния значений Jm и Kpol проводилась идентификация уравнения первого порядка при разных видах воздействия, при разном уровне зашумления и при вариации параметров настройки Kpol, Jm. Относительная погрешность Y нормировалась по максимальному изменению значения Y в пределах всего переходного процесса.

Искалось точное аналитическое решение Уа при заданном воздействии Х. Для имитации результатов эксперимента на воздействие X и решение Уа накладывались полосы шума. Центр полосы шума Dsh совпадал с кривой аналитического решения.

Исследования показали, что оптимальными являются значения:

5< kn <8, 0.002 < Sigmsm <0.003, (2)

где kn= Jm/ Kpol.

Таким образом можно организовать итерационное управление процессом идентификации обыкновенного дифференциального уравнения последовательно увеличивая значение Kpol при фиксированном значении kn. Итерационный процесс завершается при достижении заданного значения Sigmsm [3].

Литература:

1. Челабчи В.В., Челабчи В.Н. К вопросу идентификации динамических объектов / Вторая Международная научно-практическая конференция «Спецпроект: анализ  научных исследований»: Сб. научных работ. Том 3. – Днепропетровск: НАЦ ”ЕРА”, 2005. –с. 52-55.

2. Меркт Р.В., Челабчи В.В., Челабчи В.Н. Особенности сглаживания экспериментальных зависимостей методом скользящих отрезков / Сб. научных трудов по материалам международной научно-практической конференции «Современные направления теоретических и прикладных исследований ‘2011». Том 8. Физика и математика. – Одесса: Черноморье, 2011. с.18-22.