Математика / 5. Математическое моделирование

Высоченко В.В.

Одесский национальный морской университет, Украина

Управление проекционным решением обыкновенных дифференциальных уравнений

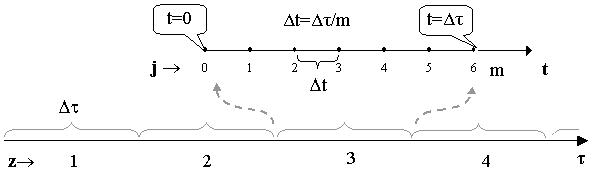
Основная идея метода заключается в том, что на отрезках Dt оси независимой переменной τ в качестве решения Y принимается функция определенного типа, но с неизвестными пока параметрами (коэффициентами). В пределах каждого отрезка Dt используется локальная независимая переменная t [1]. (Рис.1). Таким образом, создается последовательность отрезке z, каждый из которых включает достаточное количество m внутренних узловых точек j (Рис.1).

Рис. 1 Схема индексации узлов сетки при проекционном решении

На каждом отрезке проводится аппроксимация зависимости Υ(t) полиномом степени kn.

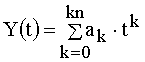. (1)

Значения коэффициента а₀ определяется из удовлетворения начальному условию или решению полученному на предыдущем отрезке интегрирования.

Выражения для функции и ее производных подставляются в решаемое уравнение. Записывается выражение для функционала S, который представляет собой сумму квадратов невязок (разностей значений правой и левой частей уравнения) для значений переменной t отнесенных к рассматриваемому отрезку. Коэффициенты аппроксимирующей функции для Υ(t) находятся путем минимизации функционала S.

Значение функционала S будет минимальным при выполнении ряда условий (7).

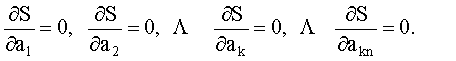(2)

Удовлетворяя каждому приведенному условию можно записать систему линейных алгебраических уравнений (СЛАУ), которая решается прямым методом.

Получение достоверного решения на каждом отрезке возможно при удачном выборе управляющих параметров m и kn. При настройке решения на каждом отрезке Dt осуществляется управляемый подбор значений kn, m с целью обеспечения желаемого уровня погрешности решения.

Для оценки эффективности проекционного решения удобно использовать среднеквадратичное значение относительной невязки s_о [1], [2].

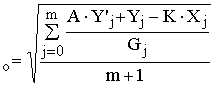, (3)

где .

Для выявления корреляции между максимальными (dYmax) и средними (dYsr) значениями относительной погрешности решения и оценкой s_o проводилось проекционное численное решения уравнения (4) при различных видах воздействия и при вариации параметров настройки Dt, kn, m. Численное решение сравнивалось с точным аналитическим решением. Относительная погрешность нормировалась по максимальному изменению значения Y в пределах всего переходного процесса.

, (4)

где А, D – заданные коэффициенты уравнения, X – воздействие.

Для выявления корреляции между максимальными (dYmax) и средними (dYsr) значениями относительной погрешности решения и оценкой s_o проводилось проекционное численное решения уравнения (4) при различных видах воздействия и при вариации параметров настройки Dt, kn, m. Численное

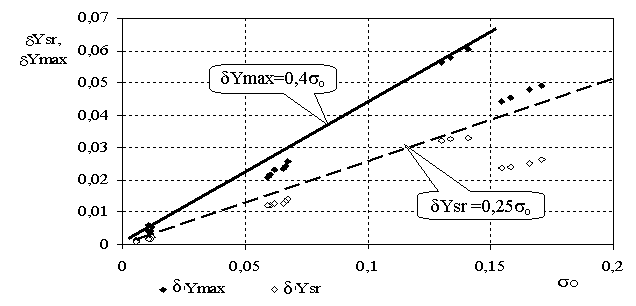
решение сравнивалось с точным аналитическим решением. Результаты исследований представлены на рис. 2.

Рис. 2 Зависимость уровня относительных погрешностей решения от s_о

На рис. 2 сплошными линиями выделены области, в которых обеспечивается заданный уровень относительной погрешности проекционного решения.

Література:

1. Челабчи В.В. Оперативное управление проекционно-сеточным методом при решении обыкновенных дифференциальных уравнений / Сборник научных трудов SWorld. Выпуск 4. Том 3. Физика и математика. – Одесса: КУПРИЕНКО, 2012 - с.49-53.

2. Меркт Р. В., Челабчи В. Н., Челабчи В. В. Организация управления решением обыкновенных дифференциальных уравнений проекционно-сеточным методом // Наука в інформаційному просторі : матеріали IX міжнар. наук.-практ. конф. , т 7.–Дніпропетровськ: Біла К.О., -2013. с. 86-90.