Математика/5. Математическое моделирование

К.э.н.Шевченко Н.Ю

Донбасская государственная машиностроительная академия, Украина

принятие решений в условиях неопределенности на основе модели статистической игры

Организация сбыта в системе предприятия и его управления играет весьма важную роль в том смысле, что осуществляет обратную связь производства с рынком, является источником информации о спросе и потребностях потребителей, что актуализирует разработку сбытовой стратеги предприятия [1].

Cбытовые стратегии условного предприятия для продвижения своей продукции на отмеченных сегментах рынка представим следующим образом:

– продажа через торговую сеть предприятия (стратегия 1);

– реализация товара через оптовых покупателей (стратегия 2);

– реализация товара через предприятия, работающие по методу самообслуживания (стратегия 3).

Представим задачу выбора оптимального канала сбыта продукции в виде статистической игры [2]:

1) первый игрок – руководство предприятия (ЛПР), выбор стратегии которого базируется на множестве взаимоисключающих стратегий, одну из которых необходимо выбрать;

2) второй игрок – внешняя середа или обозначенные сегменты рынка для продукции предприятия, которые формируют множество сценариев ;

3) функционал оценивания , элементы которого выступают количественной оценкой эффективности сбытовой стратегии в условиях рыночного сегмента .

Функционал оценивания будет иметь вид:

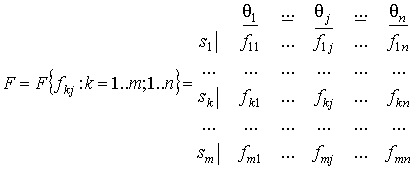, (1)

где – количественная оценка стратегии в условиях сегмента ;

– количество стратегий ();

– количество сегментов рынка (=5);

, (2)

– доля в общем годовом объеме реализации продукции в зависимости от стратегии и сегмента ;

– годовой объем реализации продукции на каждом сегменте рынка , тыс.грн;

– затраты на рекламу в зависимости от стратегии и сегмента , доли;

– затраты на сбыт (включая оплату посреднических услуг) в зависимости от стратегии и сегмента , доли.

Далее для выбора оптимальной стратегии целесообразно использовать несколько критериев выбора оптимальной альтернативы, с учетом того что решение принимается в условиях риска [2]:

– критерий Байеса (показывает средний выигрыш при условии наличия вектора вероятностей выбора сегмента , ):

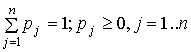, (3)

где 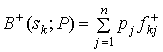– математическое ожидание эффективности альтернативы ;

– критерий минимальной дисперсии (показывает стабильность получения среднего выигрыша):

, (4)

где 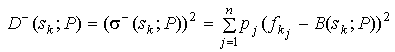– дисперсия эффективности решения ;

– критерий Вальда (получение гарантированного результата):

; (5)

– критерий доминирующего результата (оптимистический результат):

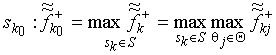; (6)

– критерий минимального риска Севиджа (оценка риска недополучения возможной прибыли):

, (7)

. (8)

Каждый из критериев дает представление об оптимальной альтернативе в различных ситуациях принятия решений, показывая возможный размер прибыли в случае выбора руководством предприятия определенной стратегии сбыта при обозначенном сегменте рынка.

Трудность заключается в формировании вектора вероятностей выбора сегмента , что выступает в качестве состояний внешней среды в ситуации выбора оптимальной стратегии сбыта.

Для формирования данного вектора воспользуемся методом одномерного шкалирования.

Постановка задачи: эксперты оценивали сегменты рынка с точки зрения перспективности и возможности их освоения. В качестве экспертов выступил руководящий состав предприятия. Необходимо оценить относительную важность сегментов и проверить достоверность полученных оценок.

Представим алгоритм метода [3].

Вычисляется матрица

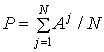, (9)

где – ранжировка, данная –м экспертом. Элемент матрицы интерпретируют как вероятность предпочтения –го сегмента –му.

Находится по формуле:

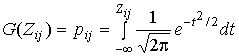, (10)

с использование таблиц нормального распределения, исходя из известных . Величина измеряется в единицах стандартного отклонения.

Образуется матрица , подсчитывается сумма оценок 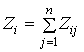и среднее значение . Величина принимается за искомую оценку объекта .

Далее определяются величины по формуле (2.10), которые нормируются по формуле:

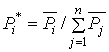, (11)

где – называют показателями относительной важности объекта.

Проверку на непротиворечивость осуществляют следующим образом: по формуле (10) находят и вычисляют разности между полученными значениями и исходными , определяют среднее отклонение:

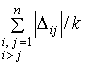, (12)

где – количество разностей.

Если 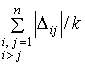мало, то это свидетельствует о непротиворечивости полученных экспертных ранжировок.

Таким образом, модель выбора оптимальной сбытовой стратегии предприятия состоит из реализации двух алгоритмов: алгоритма определения относительной важности обозначенных сегментов рынка, используемых в качестве состояний внешней среды; алгоритма выбора оптимальной стратегии сбыта на основе статистической игры. Представленная модель позволяет сформировать оптимальную стратегию поведения при организации сбыта продукции производственных и торговых предприятий. Выбор стратегии зависит от отношения руководства компании к риску.

ЛИТЕРАТУРА

1. Герчикова И.Н. Менеджмент: Учебник. – 4-е изд., перераб. и доп. – М.: Банки и биржи, ЮНИТИ, 2010. – 512 с.

2. Верченко П. І. Ризикологія: навч.-метод. посіб. для самост. вивч. дисц. / П. І. Верченко, Г. І. Великоіваненко, Н. В. Демчук. – К. : КНЕУ, 2006. – 176 с.

3. Теория выбора и принятие решений: учебное пособие. – М. : Наука. Главная редакция физико-математической литературы, 1982. – 328 с.