УДК
ӨЗАРА БАЙЛАНЫС ТЕОРЕМАСЫН ҚОЛДАНУ
АРҚЫЛЫ, ОРТАСЫНДА ДӨҢГЕЛЕК ТЕСІГІ БАР, ШЕКСІЗ
ПЛАСТИНАНЫҢ ЫҒЫСУЫ МЕН КЕРНЕУІН АНЫҚТАУ
ИСПОЛЬЗОВАНИЯ
ТЕОРЕМЫ ВЗАИМНОСТИ ДЛЯ ОПРЕДЕЛЕНИЯ НОРМАЛЬНОГО СМЕЩЕНИЯ И КАСАТЕЛЬНОГО
НАПРЕЖЕНИЯ БЕСКОНЕЧНОЙ ПЛАСТИНЫ С КРУГЛЫМ ОТВЕРСТИЯМ ВНУТРИ
USES OF THE THEOREM OF RECIPROCITY FOR
DEFINITION OF NORMAL SHIFT AND TANGENT TENSION OF THE INFINITE PLATE WITH ROUND
OPENINGS INSIDE
Аманжол А., Атшыбай
Ғ.
Е.А. Бөкетов
атындағы Қарағанды мемлекеттік университеті
Мақалада шеттік элементтер әдістері
арқылы, серпімділік теориясының жалпы шеттік есептерін жазық
қойылыммен шешу қарастырылған. Белгілі болғандай,
мұндай есептер 
контурымен шектелген 
жазық облыста
қарастырылады. 
облысы
ақырғы (облыс 
контурының
ішінде), не шексіз болуы
мүмкін (облыс 
контурынан тыс). Кез
келген жағдайда, 
контурының
әрбір 
нүктесін біз 
жанама, 
нормаль
ығысулармен және де 
жанама, 
нормаль кернеулермен
(немесе күштер) байланыстырамыз. Бұл шамалар әдеттегідей, 
нүктесінің
локальды координат жүйесімен беріледі. Біз шеттік интегралдардың тура
әдісі түрінде белгілі біршама өзгеше тәсілді
қолдандық. Осы әдіс шекарада белгісіз ығысулар мен
кернеулерді берілген шеттік шартпен тура табуға мүмкіндік береді. Бұл
әдіс өзара байланыс теоремасына негізделген
В статье рассматривается с методы
граничных элементов, предназначены для решения общих краевых задач теории
упругости в плоской постановке. Как известно, такие задачи характеризуются
плоской областью 
, ограниченной контуром 
. Область 
может быть либо
конечной (область внутри контура 
), либо бесконечной (область вне контура 
). В любом случае, с каждой точкой 
контура 
мы связываем
касательные и нормальные смещения 
, 
и касательные
и нормальные напряжения (или усилия) 
и 
. Эти величины задаются, как обычно, относительно локальной
системы координат 
точки 
. Мы используем несколько другой подход, известный как прямой
метод граничных интегралов, который позволяет находить неизвестные смещения и
напряжения на границе прямо через заданные граничные условия. В основе этого
подхода лежит теорема линейной теории упругости, называемая теоремой взаимности.
In article
it is considered with methods of boundary elements, are intended for the
solution of the general regional tasks of the theory of elasticity in flat
statement. It is known that such tasks are characterized by the flat area 
limited to a contour
of 
. The area 
can be or final (area
in a contour 
), or infinite (area out of a contour 
). Anyway, with each point of 
contours 
we connect tangent
and normal shifts of 
, 
and tangents and
normal tension (or efforts) 
and 
. These sizes are set, as usual, rather local system of
coordinates of 
of a point of 
. We use some other approach known as a direct method of
boundary integrals which allows to find unknown shifts and tension on border
directly through the set boundary conditions. At the heart of this approach the
theorem of the linear theory of the elasticity, called by the reciprocity
theorem lies.
Шеттік есеп 
облысының 
контурында 
, 
ығысулармен
және 
,
кернеулермен сипатталады делік. Әрі қарай
басқа есеп 
облысының сол 
контурында 
ығысулармен және
кернеулермен сипатталады делік. Сонда
өзара байланыс теоремасы бірінші күштер (
және 
) жүйесінің екінші (
) жылжулар
жүйесіне көбейтіндісінің жұмысы, екінші күштер (
)
жүйесінің бірінші (
,
) жылжулар жүйесі көбейтіндісінің
жұмысына тең. Мұны математикалық түрде былай
жазуға болады:
, (1)
мұнда интегралдау
барлық 
контуры бойынша орындалады.
Егер бірінші (штрихталмаған)
есептің шешімі белгісіз, ал екінші
(штрихталған) есептің шешімін білгілі болсын. Бұл
екінші есептің шешімін бақылау, немесе тестілік шешім деп атайтын
боламыз.
Енді бұрын шеттік элементтерді
талқылаған әдістердегі сияқты, бір-біріне түзу сызықты
кесінділермен жанасқан 
элементтердің көмегімен, 
контурын аппроксимациалауға болады делік.
Сонда (1) теңдеуін мына түрде ұсынуға болады [1]:
, (2)
Мұнда 
ұзындығы 
тең j-ші
кесінді. Егер әрі қарай қарастырылған есеп үшін
шекарадағы ығысу мен кернеуді әр кесінді шектеуінде
тұрақты деп алсақ, онда (2) келесі теңдік орынды:
, (3)
мұнда 
, 
және 
, 
— 
-ші кесіндінің ортасындағы кернеу мен
ығысудың мәні.
Кесінділер саны (шеттік элементтер) 
-ге тең болғандықтан, біз
соңында 
, 
және 
, 
шеттік 
параметрді аламыз.
Олардың жартысы шеттік шарттармен берілген, біз оларды
қанағаттандырғымыз келеді, ал басқа жартысы –
белгісіздер, біз оларды табуымыз керек. Әзірше бізге сонымен қатар
тестілік есептің (
, 
және 
, 
) шешуі белгілі
делік, (3) теңдеуде 
белгісіздер бар екенін көріп
тұрмыз. Осыдан, осы белгісіздерді табу үшін (3) теңдеуге
ұқсас тағы
теңдеу қажет. Басқаша айтқанда,
берілген 
облысы үшін әртүрлі 
бақылау шешімдері болу керек.
Енді шекарада әрбір 
-ші элементтің ортасында шоғырланған 
жанама мен 
нормаль күшін түсіріп,
қажетті 
бақылау шешімдер жүйесін
табуға болатыны көрсетеміз.
Алдымен 
бақылау шешімдері
шоғырланған жанама 
, 
күштеріне жауап
береді деп санап, (3)-ді былай жазамыз:
(4)
Сол сияқты 
бақылау шешімдері үшін
шоғырланған нормаль 
, 
күштеріне жауап беретін
(5)
теңдеуді ескеріп, (4)
және (5) теңдеулерін келесі түрде ұсынуға болады:
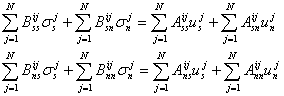, (6)
мұнда 
1-ден 
-ге дейін мәндерді қабылдайды,
ал әсер
етудің коэффициенттерін бақылау шешімдері арқылы есептеп
алуға болады [2].
Шеттік
интегралдардың тура әдісінде шеттік әсер ету коэффициенттерін
шоғырланған күштерді (
,
құраушылармен) 
контурының 
-ші кесіндісінің орта нүктесіне түсіру
және (4) пен (5)-ке сәйкес 
-ші кесіндінің бойындағы осы күштен
болған ығысу мен кернеуді интегралдау жолымен алады. 
-ді 1-ден 
-ге дейін,
яғни 
шоғырланған күштерді контур бойынша кезек-кезек
ескеріп, қажетті (6) алгебралық теңдеулер жүйесін
аламыз. 
әсер ету коэффициенттерін есептегенде (6)-де
қолайлылық үшін басы 
контурының 
-ші кесіндісінің ортасында 
, 
жергілікті координат жүйесін
қолданамыз (1-сурет). Біз 
-ші кесіндісінің ортасына түсірілген шоғырланған
күш әсерінен болған
-ші кесіндідегі ығысу мен кернеуді есептейміз (1-сурет
[
] нүктесі). Бұл күштердің i-ші кесіндеге параллель және перпендикуляр
құраушылары сәйкесінше 
, 
тең. 1-суреттен 
және
бағыттағы күштің
құраушылары келесі өрнектермен анықталатынын оңай
көруге болады:
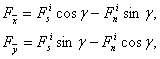(7)
мұнда 
.
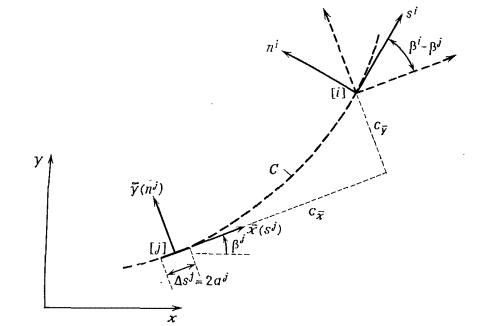
1-сурет. Шеттік
интегралдардың жергілікті координатын анықтау.
,
нүктесіне, яғни [
] (1-сурет) нүктесіне түсірілген, 
,
күшінен болған ығысу мен
кернеу өрнегін жазуға болады.
Шеттік
интегралдардың тура әдісін мысалмен сипаттау үшін шексіздікте
бір өс бойымен созылып тұрған шексіз пластинкадағы дөңгелек
ақау туралы есепті қарастырайық. Дөңгелек
ақау туралы есеп шекараның төрттен бірін жуықтайтын 25
шекаралық элемент кезінде TWOBI программасын қолдану арқылы
шығаруға болады [3]. Есепте 
, мұнда 
— шексіздікке созатын
кернеудің мәні. Бұл есеп – кернеуде шеттік есеп
болғандықтан (TWOBI-да күштік шеттік қосымша кернеу
үшін), белгісіздер 
және 
ығысулары болып табылады. 1- кестеде [3] әдебиетте қарастырылған
есептің шешуімен мақалада қарастырылған есептің
шешулері салыстырылған.
1-Кесте.
Ақау шекарасының радиалды және тангенциалды ығысуы
(TWOBI)
|
( |
|
|
||
|
Қарастырылған есеп (n=25) |
Аналитикалық
шешім |
Қарастырылған есеп (n=25) |
Аналитикалық
шешім |
|
|
0,02 0,06 0,10 0,46 0,50 0,54 0,90 0,94 0,98 |
894 883 863 333 252 171 —360 —380 —390 |
899 888 868 331 250 169 —368 —388 —399 |
—41 —120 —198 —638 —643 —638 —198 —120 —41 |
—41 — 122 —201 —605 —650 —645 —201 — 122 —41 |
Әдебиеттер
тізімі
1.
Снеддон И.Н. Преобразование Фурье. – М.:ИЛ, 1951г.
2.
С.Крауч, А.Старфилд Методы граничных элементов в механике твердого тела:
Пер. С англ.- М.:Мир, 1987.-
328с.,ил.
3.
Бреббиа К., Уокер С. Применение метода граничных элементов в технике.-
М.:Мир, 1982.
4.
Громадка II Т., Лей Ч. Комплексный
метод граничных элементов в инженерных задачах: Пер. с англ. — М.: Мир,
1990. — 303 с, ил.
5.
Бенерджи П., Баттерфилд Р. Методы граничных элементов в прикладных науках. — М.: Мир, 1984.
References
1. Sneddon I.N. Fourier
transforms, 1951. –McGraw-Hill, 1951.
2. S. Crouch,
A.Starfild Metody of boundary elements
in mechanics of a solid body: Lane.
With English - M.:World, 1987.
– 328p.
silt.
3. Brebbia C. Walker S. Application of a method of
boundary elements in equipment. - M.: World, 1982.
4. Gromadka II T., Pour H. Complex method of
boundary elements in engineering tasks: The lane with English — M.:
World, 1990. — 303 p, silt.
5. Benerdzhi P.,
Batterfild River. Methods of boundary elements in applied sciences. — M.:
World, 1984.