ЛОГИСТИЧЕСКАЯ КРИВАЯ

ПРИ АППРОКСИМАЦИИ КИНЕТИЧЕСКИХ ПРОЦЕССОВ

В ГЕТЕРОГЕННЫХ СИСТЕМАХ

Данилов А.М., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Материаловеды для аппроксимации кинетических процессов в гетерогенных системах используют логистическую кривую [1]:

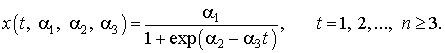
Оценим возможность такой аппроксимации.

Имеем:

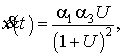
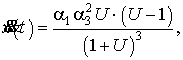
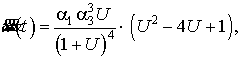
где .

Абсцисса точки B перегиба

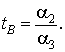(1)

Значение не зависит от a₂ и a₃, и при любых их значениях

. (2)

При любом a₃

. (3)

Условия (2), (3) дают ограничения использования логистической кривой при аппроксимации кинетических процессов [2] (во многих случаях ).

Существуют и другие ограничения. Действительно, абсциссы точек A, C определяются из условия , что дает

Откуда

,

то есть

или

Откуда

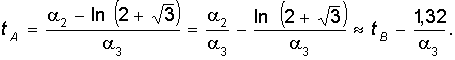
Аналогично

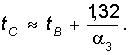
Как видим, точки A и C симметричны относительно точки B. При этом

.

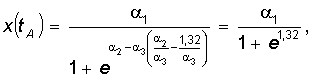
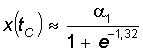Как видим, , также не зависят от a₂, a₃.

Отметим, что точка A будет находиться в правой полуплоскости тогда и только тогда, когда

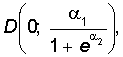
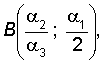
Из вышеизложенного следует, что логистическая кривая проходит через точки 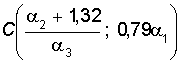и через точку 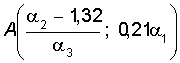при ); рис.1.

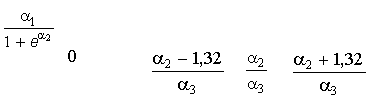
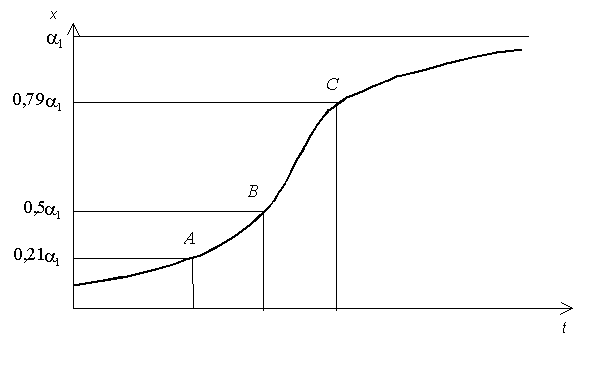
Рис. 1. Характерные точки логистической кривой

Указанные ограничения учитывались при разработке модели кинетического процесса набора прочности радиационно-защитного композита.

Литература

1. Демиденко Е.З. Оптимизация и регрессия монография. – М.: Наука. - 1989. – 296 с.

2. Данилов А.М., Гарькина И.А., Домке Э.Р. Математическое и компьютерное моделирование сложных систем. – Пенза: ПГУАС, 2011. – 296 с.