К.т.н., доцент Абрамов
П.Б.
Военно-воздушная
академия им.проф.Н.Е.Жуковского и Ю.А.Гагарина, Россия
Альтернативный
подход к моделированию систем
массового обслуживания на основе марковских форм
Моделирование систем массового обслуживания (СМО) в настоящее время приобретает все большую актуальность. Это обусловлено прежде всего тем фактом, что современные системы и сети передачи и обработки информации по своей сути являются системами массового обслуживания.
Альтернативным классическому подходу к моделированию систем массового обслуживания является применение марковских форм с внешними потоками событий. Для n-канальной СМО с отказами структурный граф подобной модели имеет вид, приведенный на рисунке 1.
Рис.1. Структурный граф n-канальной СМО с отказами
Здесь каждая вершина графа отвечает отдельному структурному элементу (каналу) системы. Между ними перемещаются потоки заявок на обслуживание. Автором в ряде трудов [1-3] показано, что для этой модели справедливы модифицированные дифференциальные уравнения Колмогорова-Чепмена. Начальные условия для задачи Коши в данном случае принимаются нулевыми. В [1] доказаны теоремы о существовании, единственности и устойчивости решения предложенного аналитического описания динамики системы.
В стационарном режиме для каждой из вершин графа может быть записано условие равенства сумм входящих и выходящих потоков событий:
. (1)
Это уравнение получается из соответствующего дифференциального уравнения при равенстве производной нулю. Отсюда имеем:
; 
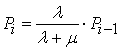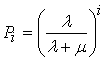. (1)
Отношение, возводимое в степень, всегда меньше единицы, поскольку величина μ в модели не равна нулю. Следовательно, справедливо соотношение 1 > P1 > P2 > P3 >…> Pn > 0, кроме того
(2)
Можно сделать вывод, что все величины Pi в полной мере удовлетворяют требованиям, предъявляемым к вероятности по определению.
Основная особенность состоит в том, что события, которым отвечают вероятности Pi, не составляют полную группу, а сумма вероятностей не равна единице, как это имеет место в классической теории. Вероятность отказа СМО в целом равна вероятности такого события, что занятыми окажутся все каналы:
, (3)
где ρ = λ/μ – нагрузка СМО.
В классической теории СМО выражение (3) трактуется как вероятность отказа n независимых одноканальных СМО. Это не вполне верное утверждение. Адекватным представлением n независимых одноканальных СМО будет модель на основе графа, приведенного на рисунке 2.
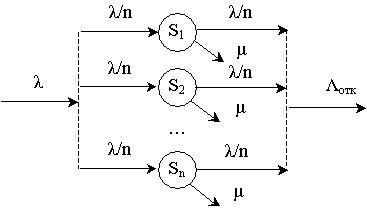
Рис.2. Структурный граф n независимых одноканальных СМО
Здесь входящий поток сначала равновероятно делится на n потоков интенсивностью λ/n, а затем каждый из этих новых потоков направляется в отдельную СМО. Заявка в i-ой СМО может получить отказ даже тогда, когда все остальные свободны. Суммарная интенсивность исходящего потока равна
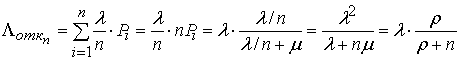. (4)
Вероятность отказа составит:
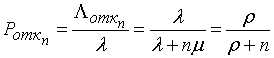. (5)
С учетом того факта, что относительная пропускная способность СМО определяется как q=1-Pотк, окончательно имеем следующие оценки:
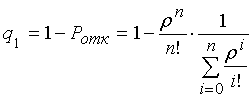– согласно классической
теории; (6)
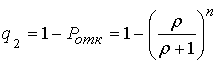– для структурной модели; (7)
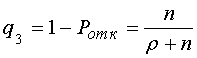– для n независимых
одноканальных СМО. (8)
Сравнение результатов для 10-канальной СМО приведено на рисунке 3.
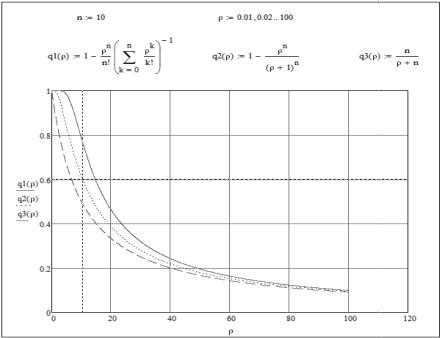
Рис.3. Зависимость пропускной способности СМО от нагрузки ρ.
Можно видеть, что асимптотика функций при ρ→∞ одинакова. Вместе с тем, на рабочем склоне характеристики существенно отличаются. Согласно предложенным оценкам (7) вероятность обслуживания потока в n-канальной СМО может превышать вероятность обслуживания потока в n одноканальных СМО (8) на величину ΔР1=0,1, что объясняется возможностью передачи заявок между каналами в случае их занятости.
В то же время классическая теория (6) повышает эту оценку еще на ΔР2=0,2, что нежелательно. Из инженерной практики общеизвестно правило о необходимости предусматривать 15-20% запас пропускной способности системы. Следовательно, применяя предложенный структурный подход, мы получаем более адекватные оценки. Кроме того, модель с незамкнутыми входами и выходами позволяет легко наращивать анализируемую структуру, выстраивая модели многофазных СМО и даже сетей массового обслуживания.
Литература:
1. Абрамов П.Б. Основы теории марковских форм с внешними потоками событий [Текст]: монография / П.Б.Абрамов – Воронеж: «Издательско-полиграфический центр «Научная книга». – 2014. – 185с.:ил. ISBN: 978-5-4446-0373-4.
2. Абрамов П.Б. Модель стационарного режима динамики средних с внешними потоками событий // Приборы и системы. Управление, контроль, диагностика. – 2012. – №6. – С.43—49. ISSN: 2073-0004
3.
Абрамов П.Б., Чурсин М.А. Анализ существования и устойчивости решения для
марковских моделей разомкнутых систем массового обслуживания. // Вестник
Воронежского Государственного университета, Серия: Системный анализ и
информационные технологии. – 2012. – №1. – с.56-61. ISSN: 1995-5499.