Д.ф.-м.н. Игошин В.А., магистрант Кузин А.М.

Нижегородский государственный технический университет
им. Р. Е. Алексеева

Инфинитезимальные симметрии квазиплоскости

В докладе сообщается о результатах, примыкающих к многолетним исследованиям первого автора, посвященным проблеме геометризации физических полей, или – что почти одно и то же - проблеме создания единой теории поля; точнее сказать – теории единого поля. На этом пути отметим два великих открытия. Это, во-первых, принцип наименьшего действия Мопертюи-Эйлера-Лагранжа-Якоби (VIII – IX века), согласно которому траектории консервативной динамической системы с любым фиксированным уровнем полной энергии совпадают с геодезическими линиями римановой метрики (без кручения) в форме Якоби. При этом кинетическая энергия моделируется римановой метрикой, а геометрическим эквивалентом потенциальной служит коэффициент конформности между кинетической энергией и метрикой Якоби. Во-вторых, это – специальная и общая теории относительности (СТО и ОТО, соответственно), созданные А. Эйнштейном в начале прошлого столетия. В рамках ОТО гравитация оказалась эквивалентом кривизны псевдориманова пространства (без кручения).

Евклидова плоскость изучается почти два с половиной тысячелетия, начиная с Евклида – создателя «евклидовой геометрии». Характеристическим свойством, выделяющим в классе римановых пространств произвольной размерности подкласс так называемых плоских пространств является обращение в нуль 4-валентного тензора кривизны риманова пространства. К таким пространствам относится евклидова плоскость. Другая важная характеристика римановых пространств – кручение, а – точнее – 3-валентный тензор кручения. Пространствам без кручения посвящены работы многих математиков, таких как Э. Картан, Софус Ли, Т. Леви-Чивита, Каган В.Ф., Солодовников А. С., Рашевский П. К., Шапиро Я. Л., Игошин В. А. и другие. Эти пространства активно применялись и применяются в физике.

Римановы пространства с кручением введены Э. Картаном в 1922 году. Они остаюся практически забытыми. В отличие от кривизны кручение является «вещью в себе» для многих математиков, даже специалистов – геометров. Недавно геометрией «крученых» пространств заинтересовался Игошин В.А. в связи с классической проблемой геометризации физики. Ему удалось построить геометрическую модель: 1) постоянного магнитного поля (см. материалы международной научно-технической конференции «Информационные системы и технологии (ИСТ-2012)», Нижний Новгород), 2) постоянного электрического поля (см. материалы конференции ИСТ-2013). Геометрическим эквивалентом поля оказался тензор кручения; кривизна же, в отличие от модели ОТО, обращается в нуль. Эти результаты показывают, что крученые пространства играют существенную роль в проблеме геометризации физики. Именно поэтому их исследование приобретает приоритетный характер.

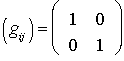2. Ниже речь идет о некоторых аспектах геометрии квазиплоскости – крученой евклидовой плоскости. Метрический тензор собственно евклидовой плоскости совпадает с тензором Кронекера, задаваемым единичной матрицей Грама . При заданном тензоре кручения функции метрической связности выражаются через этот тензор: .

В геометрии пространств аффинной связности важную роль играют так называемые движения (симметрии) таких пространств, как конечные (дискретные), так и бесконечно малые (непрерывные). Последние задаются векторными полями и носят название инфинитезимальных движений. Существуют различные классы симметрий: аффинные движения, сохраняющие связность; геодезические движения, сохраняющие геодезические линии связности вместе с каноническим параметром на каждой из них; проективные движения, сохраняющие геометрические (непараметризованные) геодезические.

Имеются так называемые уравнения С. Ли инвариантности, соответствующие тому или иному геометрическому объекту. Случай аффинных движений изложен в материалах ИСТ-13.

Далее сообщается о результатах, относящихся к геодезическим и проективным симметриям. Для этих классов движений, аналогично предыдущей работе (ИСТ-2013), найдены алгебры Ли указанных выше симметрий квазиплоскости – двумерного евклидова пространства с наперед заданным постоянным тензором кручения : 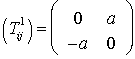, , 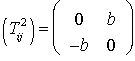где a, b – произвольные константы.

Коэффициенты любой аффинной связности, можно представить в виде суммы двух частей: , где первая получается симметрированием по нижним индексам, вторая – альтернированием. Полученные симметрированием слагаемые являются компонентами новой связности без кручения, геодезические линии которой совпадают с таковыми для связности . Поэтому уравнения С. Ли геодезических инфинитезимальных движений квазиплоскости имеют вид:. В результате довольно громоздких вычисления (которые здесь не приводятся) получается следующая система уравнений С .Ли, состоящая из шести дифференциальных уравнений в частных производных 2-го порядка:

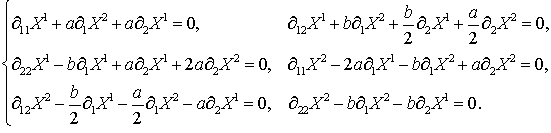
Решив эту систему дифференциальных уравнений, получим искомое общее решение в виде множества всевозможных постоянных векторных полей на нашей крученой плоскости: .

Для нахождения алгебры Ли проективных движений нами вычислены проективные параметры Томаса: .

_{В итоге система дифференциальных уранений С.Ли проективных движений приобретает следующий вид:}

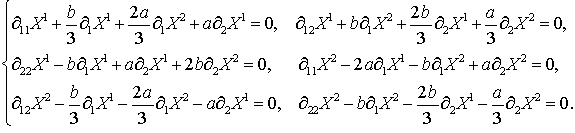
Общее решение: Это означает, что алгебры Ли инфинитезимальных геодезических и проективных симметрий крученой плоскости совпадают. Более того, как следует из нашего доклада на конференции ИСТ-13, обе эти алгебры совпадают с алгеброй Ли движений, сохраняющих параллельный перенос и метрическую связность квазиплоскости.

В заключение следует отметить, что последующие наши работы будут также посвящены геометрии квазиплоскости и, в частности, параллельному переносу, геодезическим (т.е. прямым) линиям и другим задачам «квазипланиметрии», таким как проверка выполнения аксиом собственно евклидовой планиметрии. Особый интерес представляют ответы на вопросы: какой из постулатов «о параллельных» – Евклида, или Лобачевского – осуществляется в квазиплоскости и чему равна сумма углов треугольника?

Расчет компонент алгебры Ли является трудоемкой задачей для двумерного случая с постоянным метрическим тензором и постоянным тензором кручения. В связи с этим было решено сделать программу для автоматизации данного процесса. На данный момент проделана существенная работа в данном направлении, но текущая версия программы еще не обладает всей необходимой функциональностью. Исходный код доступен для бесплатного использования и опубликован на сайте GitHub: https://github.com/Leviathan941/symmetries.

E-mail: vaigoshin@rambler.ru; amkuzink@gmail.com