Педагогические науки/5.Современные методы преподавания

К.т.н. Куимова Е.И., к.п.н. Ячинова С.Н.

Пензенский государственный университет архитектуры и строительства, Россия

Методические аспекты формирования мотивационной составляющей обучения

В процессе изучения математического анализа со студентами не технических специальностей приходиться сталкиваться с непониманием необходимости изучения многих его разделов. Для преодоления данной проблемы и стимулирования мотивационной составляющей обучения помогает демонстрация приложений изучаемого раздела соответствующая направлению подготовки студентов. Рассмотрим, как это можно сделать, на примере изучения обыкновенных дифференциальных уравнений.

Демонстрация применения дифференциальных уравнений возможна после изучения основные понятий и определений и рассмотрения основных методы их решения. Можно изучить различные модели: модель естественного роста, модель истощения ресурсов, модель роста населения Земли с учетом насыщения, модель «социальной диффузии».

Рассмотрим модель естественного роста выпуска продукции: найти закон роста выпуска дефицитной продукции в условиях не насыщаемости рынка.

Количество продукции, которая произведена в момент времени t, обозначим . Предполагаем, что продукция реализуется по фиксированной цене p моментально. Доход в момент времени t равен . Предприятию выгодно расширять производство, чтобы получать прибыль от реализации своей продукции.

Пусть на инвестиции в производство расходуется m-я часть дохода, т.е. .

Результатом расширения производства будет прирост дохода, m-я часть которого будет направлена на увеличение выпуска продукции. Это приведет к росту выпуска, причем скорость выпуска будет пропорциональна увеличению инвестиций, т.е. .

Таким образом, получим дифференциальное уравнение естественного роста

,

.

Решением которого является экспоненциальная функция , показывающая, как можно быстро добиться огромных объемов выпуска дефицитной продукции, если постоянно направлять часть дохода в расширение производства.

Харрод и Домар считали, что можно добиться устойчивого роста всей мировой экономики, так как устойчивый темп роста производства обеспечивается естественным ростом населения, естественным ростом производительности труда и увеличением размера накопления капитала.

Модели естественного роста описываются экспоненциальной функцией. В связи с тем, что темпы роста, описываемые экспоненциальной функцией, со временем замедляются, и наступает период насыщения, возникла необходимость в изменении самой модели роста.

Дж. Кьютелет считал, что константа в уравнении естественного роста должна быть убывающей функцией, зависящей от : .

Основываясь на это предположение, в 1836 г. его ученик Ферхюльст для модели роста населения предложил использовать уравнение

,

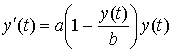т.е. считать, что

.

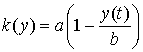Разделяя переменные, находим

,

.

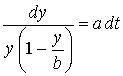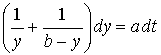Проинтегрировав это соотношение, получаем

,

.

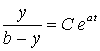Отсюда следует, что .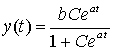

Полученную функцию называют логистической кривой. При малых значениях t логистический рост подобен естественному росту, а при больших t характер роста изменяется и темпы роста замедляются. При кривая приближается, но не пересекает прямую , которая является стационарным решением уравнения и соответствует случаю

.

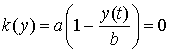Модель Ферхюльста применяется и к другим социально-экономическим явлениям.

Таким образом, демонстрация возможности применения дифференциальных уравнений обеспечивает усиление мотивационной составляющей учебного процесса и существенно влияет на усвоение студентами данного раздела математического анализа. Интерпретация экономических и социальных процессов с помощью математического языка подготавливает студентов к моделированию реальных процессов. Кроме того, способствует формированию системы знаний и операционных умений, используемых для решения задач, возникающих при выполнении основных видов профессиональной деятельности и развитию личностных качеств, необходимых для высококвалифицированных специалистов.