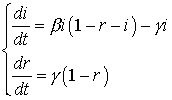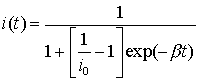Современные информационные технологии/2 Вычислительная техника и программирование
Лесько С.А.
Московский государственный университет приборостроения и информатики.
Россия
Моделирование динамики
эпидемий вирусов в компьютерных сетях на основе дифференциальных кинетических
уравнений
Исследование и
математическое моделирование динамики компьютерных угроз является ещё
сравнительно молодой и развивающейся областью информатики. Однако следует
отметить, что несмотря на актуальность исследования динамики информационных
угроз в настоящее время существует только две основные модели [1-5] развития
компьютерных эпидемий, берущие своё начало из биологии. Вместе с тем, хотя
полученные результаты и позволяют выработать определённую стратегию
антивирусной защиты [6,7], но анализ сетевых эпидемий последнего времени не
позволяет быть уверенным относительно эффективности применяемых мер защиты,
разрабатываемых на основе моделирования динамики угроз с помощью существующих
моделей. На это в частности указывают результаты работ, в которой (на основе
анализа имеющихся данных наблюдений и моделирования эпидемий таких червей
(вирусов) как Code Red I, Code Red II, Nimda и Slammer [8-11]) была
разработана концепция Warhol
червя (мгновенный вирус) [10,11]. Таким образом, можно
сделать вывод, что для обеспечения результативных мер безопасности необходимо
продолжить построение новых теоретических моделей описания динамики
информационных угроз и анализ на их основе существующих уязвимостей.
Одна из существующих
моделей описывает развитие эпидемии в сетях без защиты (так называемая SI-модель), а вторая с учётом действия
антивирусов (SIR-модель).
Модель SI
[1-5] исходит из того, что любой их входящих в атакуемую сеть компьютеров может
находиться в одном из двух состояний: уязвимом (S) и инфицированном (I), причем
общее число компьютеров в сети N=I+S. Данная модель основывается на уравнении:
|
|
|
(1)
|
где i – доля
зараженных компьютеров, β – константа скорости размножения вирусов.
В модели SIR факторы, обеспечивающие затухание сетевых эпидемий,
оцениваются исходя из того, что сетевые узлы могут находится в трех состояниях:
уязвимом (S), зараженном (I) и невосприимчивом (R).
Отметим, что узлы оказываются неуязвимыми только после излечения от инфекции, а
N – бщее число узлов сети
равно S+I+R. Вводя постоянную среднюю скорость
«иммунизации» в единицу времени γ, для описания динамики развития
эпидемий, можно получить следующую
систему уравнений [1-5]:
|
|
|
(2)
|
В одной из
модификаций модели SIR
кроме того, рассматривается еще возможность прироста сети, с постоянной
скоростью, за счет появления новых узлов. При распространении эпидемии быстрота
заражения сети в значительной степени определяется стратегией поведения
вирусов. Если происходит рассылка копий вирусов по случайно выбранным адресам,
то скорость заражения сети снижается по сравнению с вариантом, когда адресное
пространство сети было первоначально разделено между вирусами. В модели SI случайное
распространение, или целенаправленное распространение вирусов учитывается
эмпирическим образом за счет уменьшения или увеличения константы скорости
β их размножения.
В
представленной работе предлагается модель, в которой возможность замедления
распространения эпидемии (в результате случайного выбора адреса в сети) уже
заложена изначально. Суть этой модели заключается в следующем: при
лавинообразном распространении, каждый из вирусов, образовавшийся на каком-либо
шаге процесса размножения на следующем (h+1) шаге рассылает некоторое число
своих копий, каждая из которых способна с равной вероятностью заразить любой из
незараженных компьютеров.
Пусть
коэффициент размножения вирусов равен ξ, а общее число компьютеров в сети
равно L. Тогда изменение на (h+1) шаге числа инфицированных компьютеров будет
равно Ph+1-Ph (где Ph+1 – число компьютеров
инфицированных на (h+1) шаге, а Ph – число инфицированных
компьютеров на шаге h). С другой стороны, если гибели вирусов не происходит, то
изменение числа заражённых компьютеров на (h+1) шаге должно быть равно
произведению числа Ph инфицированных на шаге h компьютеров на
коэффициент размножения вирусов ξ и вероятность ![]() того,
что каждый из появившихся на (h + 1) шаге вирусов попадет на незараженный
компьютер.
того,
что каждый из появившихся на (h + 1) шаге вирусов попадет на незараженный
компьютер.
|
|
|
(3)
|
Если длительность
каждого шага равна τ, то можно ввести переменную t, задающую время
процесса t = h∙τ и тогда перейдя от числа шагов h к времени t
получим:
|
|
|
(4)
|
Разложим P(t +
τ) (считая τ – бесконечно малым) в ряд Тейлора:
|
|
|
(5)
|
Разделив
уравнение (4) на L и τ и учитывая, что ![]() и
и ![]() , и обозначив все производные выше первого
порядка как
, и обозначив все производные выше первого
порядка как ![]() получим:
получим:
|
|
|
(6)
|
Уравнение (6)
отличается от уравнения (1) наличием члена вида ![]() ,
учитывающим, что часть рассылаемых вирусов попадает на уже зараженные машины,
что приводит к уменьшению скорости заражения
,
учитывающим, что часть рассылаемых вирусов попадает на уже зараженные машины,
что приводит к уменьшению скорости заражения ![]() .
.
Предполагая, что
в начальный момент времени t0 = 0 доля инфицированных узлов
составляет i0, решение уравнения (1) имеет вид:
|
|
|
(7)
|
Уравнение (7) –
является логистической функцией, из анализа данных по наблюдению червя Code Red v2, приведенных в [10] данных
следует, что для Code Red v2 i0 ~10–11…10–10,
т.е. можно предполагать, что червь начинал атаку на сеть не более чем с одного
компьютера. Не останавливаясь на модели SI подробно рассмотренной в ряде работах [1-5],
сравним аналитическое решения уравнения (7) и численное решение уравнения (6)
при одинаковых значениях параметров τ, L, P0 и ξ
представленные на рис. 1.
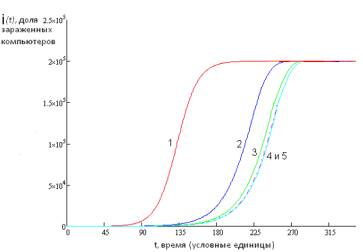
Рисунок 1. Сравнение решения уравнения (7) кривая 1, с
решением уравнения (6). Кривая 2 с учетом второй производной, кривая 3 с учетом
третьей производной, кривая 4 с учетом 4-ой производной и кривая 5 с учетом
пятой, для одинаковых значениях параметров (τ = 25, L = 200000, P0 = 5 и ξ
= 2).
Представленные на
рис. 1 данные показывают, что при учете в модели, описывающей динамику
распространения вирусов, производных выше первого порядка, наблюдается
замедление их распространения, по сравнению с моделью SI описываемой уравнением (7). Следует
отметить, что результаты, полученные с учетом четвертой и пятой производных,
имеют малые отличия, а, следовательно, производные более высоких порядков уже
можно не учитывать.
Таким образом,
полученная модель позволяет описать, как распространение вирусов при случайной
рассылке по адресам, так и при разделении адресного пространства сети и учете
вирусами уже использованных адресов. При рассмотрении второго случая, параметры
процесса будут определяться не только тем, как вирусы распределяют адресное
пространство сети, но и как они сообщают друг другу о использованных адресах.
В реальной
ситуации всегда появляется антивирус, который борется с вирусами, поэтому
интересно проанализировать динамику эпидемии при наличии защиты. Процесс
распространения вирусов всегда начинается несколько раньше, чем они будут
обнаружены и появится эффективный антивирус способный их необратимо уничтожить,
т.е. антивирусы появляются только на некотором шаге процесса распространения
вирусов отстающим от начала их распространения на h0 – шагов, т.е.
на шаге k=h–h0 (происходит запаздывание). Число антивирусов
появляющихся на (h+1) для вирусов или для самих себя на (k+1) шаге обозначим
как Nk+1, а появившихся на k-шаге (шаге h для вирусов) как Nk.
Число зараженных на (h+1) шаге компьютеров можно обозначить как Ph+1,
а зараженных на шаге h, как Ph. Изменение числа инфицированных равно
разности числа заражений и числа уничтоженных вирусов антивирусом на h+1 шаге.
Имеются следующие случайные события, образующие полную систему: Компьютер
заражен вирусом с вероятностью ![]() (Ph
– число вирусов на шаге h, L – число компьютеров в сети). На компьютере с
вероятностью
(Ph
– число вирусов на шаге h, L – число компьютеров в сети). На компьютере с
вероятностью ![]() имеется антивирус, с вероятностью
имеется антивирус, с вероятностью ![]() нет
ни вируса, ни антивируса.
нет
ни вируса, ни антивируса.
Число заражений
на (h+1) шаге составит: ![]() т.к.
заражение уже зараженного компьютера не происходит, а компьютер на котором есть
антивирус заразится не может. Число уничтожений вирусов на (h+1) шаге должно
составить
т.к.
заражение уже зараженного компьютера не происходит, а компьютер на котором есть
антивирус заразится не может. Число уничтожений вирусов на (h+1) шаге должно
составить ![]() , где
, где ![]() –
вероятность того, что на (h+1) шаге любой из Ph – вирусов,
существовавших на шаге h, может встретить антивирус. Таким образом:
–
вероятность того, что на (h+1) шаге любой из Ph – вирусов,
существовавших на шаге h, может встретить антивирус. Таким образом:
|
|
(8) |
Изменение на
(k+1) шаге числа компьютеров, на которых установлен антивирус, определяется
разностью Nk+1–Nk, где Nk+1 – число машин с
антивирусом на (k+1) шаге, Nk – число машин с антивирусом на шаге k.
С другой стороны
Nk+1–Nk должно быть равно:
|
|
(9) |
где
ξ∙Ph учитывает, что антивирус устанавливается на (h+1)
шаге на тех машинах, на которых на шаге h был обнаружен вирус, а ![]() учитывает, что антивирус устанавливается только там, где его ранее
не было.
учитывает, что антивирус устанавливается только там, где его ранее
не было.
Учитывая, что
длительность каждого шага равна τ, то все время процесса t=h∙τ,
а t0=h0∙τ, (k=h–h0). Переходя от
числа шагов h и k ко времени процесса t,
и учитывая, что t-t0=y, разложив (1) и (2) в ряд Тейлора и
ограничившись не более чем первыми производными получим:
|
|
(10) |
|
|
(11) |
Уравнения (10) и
(11) образуют систему уравнений, которая существенным образом отличается от
системы уравнений (2), используемой в модели SIR (S – уязвимости, I –
инфицированные, R – излеченные), которая в ряде случаев более адекватно
описывает результаты наблюдений. Основная суть отличий полученной модели от
модели SIR заключается в следующем:
1.
В уравнении (10)
убыль вирусов в правой части определяется произведением числа вирусов на
вероятность их встречи с антивирусом, в том время, как модель SIR говорит об убыли происходящей с постоянной
средней скоростью не зависящей от числа антивирусов.
2.
В предлагаемой
модели скорость изменения числа антивирусов связана с числом вирусов, имеющихся
в данный момент (уравнение (11)). В модели SIR скорость появления антивируса постоянная и
не зависит от числа вирусов.
Численное
решение системы уравнений (10) и (11) позволяет получить зависимости,
моделирующие цепной процесс распространения вирусов, когда в определенный
момент времени t = t0 начинает действовать антивирус.
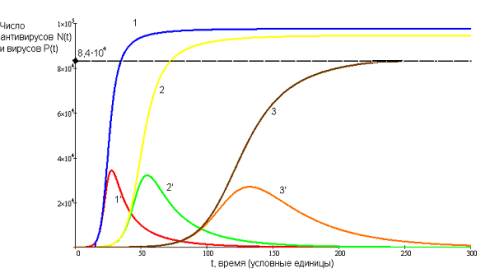
Рис.2 Результаты численного решения системы уравнений
(10) и (11) для сети состоящей из 100000 компьютеров с P0 = 5 и τ = 25 условных единиц (кривые 1 и 1'
соответственно показывают изменение N(t) и P(t) для ξ = 10, кривые 2 и 2' для ξ = 5,
кривые 3 и 3' для ξ = 2).
При
прогнозировании вирусных атак и комплекса защитных мероприятий особый интерес
представляет время запаздывания действия антивирусного ПО. Данные моделирования
показывают, что чем позже начинает действовать антивирусное ПО тем сильнее
оказывается заражена сеть. Менее очевидным и более интересным результатом
является то, что предельное число зараженных машин увеличивается с ростом t0 – времени начала действия антивируса, но только до определённых
значений t0, а в целом оно все-таки не достигает общего
числа машин в сети.
На рисунке 2
представлены результаты численного решения системы уравнений (10) и (11) для
сети состоящей из 100000 машин, с начальным числом вирусов P0 = 5, τ
= 25 условных единиц для различных ξ, при начале действия антивируса в момент времени t0 = 15 условных единиц времени после появления вирусов. Следует обратить
внимание, что предельное число антивирусов не достигает числа компьютеров
100000, после ликвидации вирусов. Подобная картина наблюдается на практике,
когда пользователи не устанавливают антивирусное ПО после предотвращения
эпидемии, если во время эпидемии компьютеры не были инфицированы. Это может
служить причиной повторных всплесков активности вирусов, как это наблюдалось в
2000 - годах.
Литература
1. The
Workshop on Rapid Malcode (WORM), October 27, 2003, The Wyndham City Center
Washington DC, USA. (http://pisa.ucsd.edu/worm03/).
2. Jasmin
Leveille «Epidemic Spreading in Technological Networks» (http://www.hpl.hp.com/techreports/2002/HPL-2002-287.pdf).
3. C. G.
Senthilkumar «Worms: How to stop them?» (http://wwwcsif.cs.ucdavis.edu/~cheetanc/worms/proposal.ps).
4. M.
Garetto, W. Gong, D. Towsley «Modeling Malware Spreading Dynamics» IEEE INFOCOM
2003 (http://www.ieee-infocom.org/2003/papers/46_01.PDF).
5. А. А. Захарченко «Бой с тенью: компьютерные
вирусы и причины сетевого хаоса» Защита информации. Конфидент, 2003, № 6, с.
49–52.
6. John
Leyden «The trouble with anti-virus» (http://www.theregister.co.uk/content/56/32680.html).
7. Duncan
Graham-Rowe «Computer antivirus strategies in crisis» (http://www.newscientist.com/news/news.jsp?id=ns99994119).
8.
C.C. Zou, W. Gong and D. Towsley. «Code Red Worm
Propagation Modeling and Analysis» In 9th ACM Symposium on Computer and
Communication Security, pages 138-147, Washington DC, 2002. (http://tennis.ecs.umass.edu/~czou/research/codered.pdf)
9.
Sh. Gaudin «2003 'Worst Year Ever' for Viruses, Worms»
(http://www.esecurityplanet.com/trends/article.php/3292461).
10.
S. Staniford, V. Paxson and N. Weaver. «How to Own the
Internet in Your Spare Time» 11th Usenix Security Symposium, San Francisco,
August, 2002. (http://www.icir.org/vern/papers/cdc-usenix-sec02/).
11.
N. Weaver. «Warhol Worms: The Potential for Very Fast
Internet Plagues» (http://www.cs.berkeley.edu/~nweaver/warhol.html).