А.Е. Сегізбаева

№12 М.Әуезов атындағы тірек мектебі, Жамбыл облысы, Қазақстан

СЫЗЫҚТЫ АЛГЕБРАЛЫҚ ТЕҢДЕУЛЕР ЖҮЙЕСІН ШЕШУДІҢ САНДЫҚ ӘДІСТЕРІ

Сызықты алгебралық теңдеулер жүйесін шешудің тура әдістері.

Сызықты алгебралық теңдеулер жүйесін шешудің Крамер әдісі- бойынша сызықты теңдеулер жүйесін шешуде жүйелі түрде келесі алгоритм орындалады:

1. Жүйені матрицалы түрде жазады (егер бұл әлі істелмесе).

2. Жүйенің басты анықтауышын табады:

Сызықты алгебралық теңдеулер жүйесін шешудің Гаусс әдісі-Гаусс әдiсiн қолдану арқылы, жүйенi белгiсiздерiнен бiртiндеп арылады және жүйенi үшбұрыш түрiне алып келедi.Гаусс әдісінің басқа атауы шығады – белгісіздерді сатылы алып тастау әдісі.

Сызықты алгебралық теңдеулер жүйесін шешудің «Бас элементті таңдау схемасы» әдісі-Гаусс әдісінің өзгертілген түрінің бірі (модификациясының бірі) – бас элементті таңдау схемасы болып табылады. Мұнда белгісіздерді біртіндеп шығаруда бөлу орындалатын диагоналдық элементтердің нөлге тең болмау шарты одан да қатаң шартпен, яғни қалған к-шы бағандағы элементтердің ішінен модулі ең үлкені таңдалып, а_кк элементінің орнына баратындай етіп теңдеулердің орнын алмастыру қажет шарты қойылады.

Қуалау әдісі-Теңдеулер жүйесінің матрицасы үш диагоналды болған жағдайда Гаусс әдісінің модификациясы «Қуалау әдісін» қолданады. Мұндай теңдеулер жүйесі инженерлік есептерді моделдеу кезінде және дифференциалдық теңдеулердің шектік есептерін сандық әдістермен шешу кезінде пайда болады.

Теңдеулер жүйесі келесі түрде берілсін:

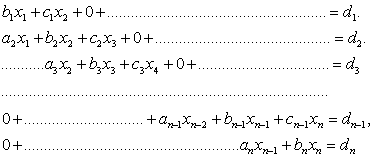
Сызықты алгебралық теңдеулер жүйесін шешудің итерациялық әдістері:

Сызықты алгебралық теңдеулер жүйесін шешудің жай итерациялық әдісі-; (2.3)

Алғаш векторынан бастап, х* нүктесіне біртіндеп жақындауды – қарапайым итерация әдісі деп атайды. тізбегінің, кезде х* нүктесіне жинақталуы үшін, (3.2) теңдеуіндегі матрицалар мен векторларға шарт қою керек.

Теорема 2.1.(2.3) қарапайым итерация әдісі, кез келген векторы үшін жылжымайтын х* нүктесіне жинақталуы үшін В матрицасының барлық меншікті мәндерінің модульдері бірден кіші болуы қажетті және жеткілікті.

Сызықты алгебралық теңдеулер жүйесін шешудің Гаусс-Зейдель әдісі-(2.2) түрдегі теңдеудің (k+1) қадымында, х векторының әрбір құраушысын анықтау кезінде, оның алында анықталған және құраушылары пайдаланылады. Итерациялық теңдеу былай жазылады:

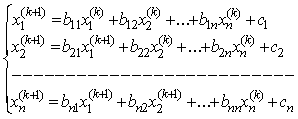(2.9)

Бұл теңдеуді матрицалық түрде жазу үшін (2.1) теңдеуінің матрицалық түрін пайдаланайық. Мұны

түрде жазып, мынандай итерациялық теңдеу аламыз:

(2.10)

немесе,

(2.11)

Зейдель әдісі, (2.7) түрдегі Якоби әдісінің дербес түрі

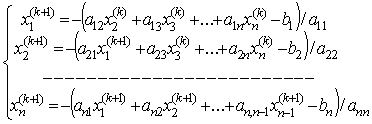
Сызықты алгебралық теңдеулер жүйесін шешудің Якоби әдісі-теңдеуіндегі А матрицасын түрде жазайық. Мұндағы D – диагональ, L және R, тиісінше сол және оң жақты үшбұрышты матрицалар. Сонда теңдеу былай жазылады:

.

Егер А матрицасының диагоналында нөлдік элемент болмаса, онда теңдеу (2.2) түріне келеді.

. (2.5)

мұндағы , деп алсақ, есепті қарапайым итерация әдісіне келтіруге болады.

Теорема. Егер А матрицасында диагональ элементтер басым болса, Якоби әдісі жинақталады.

Сызықты алгебралық теңдеулер жүйесін шешудің Релаксация әдісі.

Егер жоғарыдағы итерация әдістерінде, қателіктерді бағалау үшін қажетті, В итерация матрицасының нормасын жоғары жағынан шектейтін , немесе сандарын анықтау мүмкін болмаса, есептеуді қай кезде тоқтату керектігі белгісіз болғандықтан итерация әдісін қолдану қиындықтар туғызады. Мұндай жағдайда, итерациялық тізбектің жинақтылығын тездететін, Зейдель әдісінің жалпылама түрін қолдануға болады.

Теңдеулер жүйесіне Зейдель әдісін қолданған кездегі k-жуықтау үшін х векторының і-құраушысын деп, ал жаңа әдіс үшін k-жуықтаудағы құраушысын деп белгілейік. Релаксация әдісін мына формула арқылы анықтаймыз:

.

Сызықты алгебралық теңдеулер жүйесін гаусс және итерациялық әдістермен шешуді эем-да ұйымдастыру .

DЕLРНІ ортасында бағдарлама құру негіздері

Windows терезесі арқылы Delphi-ді іске қосу командасы:

Іске қосу-Программалар-Borland Delphi 7-Delphi 7.

Экранда Delphi ортасының үш терезесі көрінеді .

Delphi 7-тің негізгі терезесі;

Форма (Form1);

Объект инспекторы терезесі (ObjectInspector).Жоғарыда келтірілген негізгі анықтамаларды және Delphi-де бағдарлама құру негіздерін ескере отырып сызықты алгебралық теңдеулер жүйесін Гаусс және итерациялық әдістермен шешуді ЭЕМ-да ұйымдастыру алгоритмі төменде келтірілген.

Delphi ортасында негізгі қалыптың жасалуы.

Қалып,-теңдеулер жүйесінің коэффициенттері енгізуге, есептеу әдісінің бірін таңдауға, есептеуге, нәтижені сақтау және баспаға шығаруға, нәтижені, яғни шешіміді экраннан тікелей көру, жаңа есеп шығару үшін қолданылады. Қалыптың көмегімен есептеу барысына басқа да қосымша өзгерістер енгізуге болады. Қалыпта суреттер, графиктер немесе басқада жаңа енгізілген обьектілерді және мәліметтерді өңдеу үшін Паскаль тілінде жазылған процедуралар болуы мүмкін.

Жұмыста, осы айтылғандарды орындау барысында, яғни сызықты алгабралық теңдеулер жүйесін шешуді автоматтандыру үшін негізгі қалып жасалынды. Негізгі қалыпты пайдалану үшін арнайы бумада сақталған Project1.exe файлын жүктейміз. Жүктегеннен кейінгі қалып бейнесі төменде келтірілген

Кнопкалы қалып құрылғаннан кейін ондағы көрсетілген батырмалар көмегімен қажетті мәліметтерді көріп, өңдеп, өзгертіп және есептеп, нәтижені баспаға шығаруға болады. Мысалға батырмасындағы стрелкалардың көмегімен матрица размерін таңдай аламыз. Матрица коэффициенттерін енгізіп, яғни үш белгісізі бар үш теңдеулер жүйесінің коэффициенттерін енгізіп «Есептеу» батырмасын басқаннан кейінгі қалып көрінісі. Қалыптың оң бөлігінде есептеу нәтижесі көрінеді

Сызықты алгебралық теңдеулер жүйесін шешудің тура және итерациялық әдістерін үйреніп, Гаусс және Зейдель әдістерімен ЭЕМ-ның көмегімен практикалық есептерді шешуде Delphi ортасында автоматтандырылған арнайы бағдарламасы дайындалды.

Әдебиеттер:

1. Хакимова Т. Компьютерлік өңдеудің мүмкіндігін жоғарылату. Оқу құралы. – Алматы: Ғылым, 2008. – 67 б.

2. Хакимова Т. Компьютерлік өңдеудің әдістемелері. Оқу құралы. – Алматы: Ғылым, 2002. – 160 б.

3. Павлов С.П, Губонина З.И.. Охрана труда в приборостроении - М.: 1986. -264 с.

4. Навакатикян А.О., Кальнищ В.В.. Охрана рудопользователейкомпьютерных видеодисплейных терминалов, - Киев: 1997.-198 с.

5. Керри И. Праг, Майкл Р. Ирвин. Місrоsоft Ассеss2000 –Библия
пользователя», - М.: 2000. -354 с.Гельман В.Я. Решение математических задач средствами Excel, М.: Питер, 2003

6. Мсхалая Ж.И., Осипов Ю.В., Павлов А.Б. основы современной технологии, Часть 2 Excel, М., 2002

7. Бузин. А. Ю. Компьютерный АПЛ-практикум по численным методам и математическому моделированию. Москва. Издательство Российского университета дружбы народов, 2001г.

8. Алексеев Е. Р., Чеснокова О. В., Павлыш В. М., Славинская Л. В.. Турбо Паскаль 7. 0. Идеальный учебный курс. Численные методы. NT. Press. Москва, 2004г.

9. Галушко Ю. И., Тимохина А. О..Численные методы. МТИПП, 2000