Технические науки/12. Автоматизированные системы управления на производстве

К.т.н. Саушев А.В., к.т.н. Белоусова, Бова Е.В.

Государственный университет морского и речного флота

имени адмирала С.О. Макарова, Россия

Метод контроля состояния технических систем

по областям работоспособности

Основу повышения эффективности процесса эксплуатации технических систем (ТС) составляет переход к проведению технического обслуживания и ремонтов по фактическому уровню их состояния. В докладе рассматривается метод определения состояния ТС, основу которого составляет информация о границе области работоспособности. Метод обеспечивает высокую точность идентификации состояния системы и решение задачи определения ее запаса работоспособности. Полученная информация необходима для успешной работы разнообразных производственных автоматизированных систем управления.

Состояние ТС характеризуется некоторым набором или вектором параметров, среди которых можно выделить: внутренние параметры , определяющие допусковую область и характеризующие состояние комплектующих элементов ТС. Эти параметры называют также первичными параметрами системы; внутренние параметры , определяющие допусковую область , которые характеризуют фазовые переменные на выходах элементов системы, , h – число элементов; выходные параметры , определяющие допусковую область , которые характеризуют различные функциональные зависимости фазовых переменных на выходе объекта управления [1].

Область допустимых изменений параметров X (область работоспособности) определяется неравенствами:

,

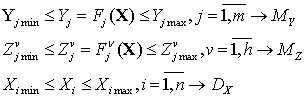где (), (), () – соответственно максимально и минимально допустимые значения j–го выходного (внутреннего ) параметра; F – оператор связи первичных параметров с внутренними и выходными Y параметрами; и – предельно допустимые значения первичных параметров. Области и являются соответственно отображением областей и в пространство первичных параметров ТС.

Задача контроля технического состояния ТС заключается в распознавании принадлежности вектора Y(t) области или вектора X(t), области G, а также в определении запаса работоспособности системы в случае, если . При этом под запасом работоспособности l понимается степень приближения вектора фактического состояния ТС к его предельно допустимому значению: . Здесь – наикратчайшее расстояние между текущим состоянием вектора X(t) и границей области G; – аналогично , но для момента времени _, что соответствует начальному моменту эксплуатации ТС.

Трудность решения задачи контроля обусловлена необходимостью построения границы области G, которая может иметь весьма сложную конфигурацию, и необходимостью вычисления величин и . Кроме того, для определения вектора требуется контролировать все n параметров X, что при большой размерности пространства весьма проблематично. Для упрощения задачи распознавания область работоспособности обычно аппроксимируют вписанным или описанным брусом наибольшего объема. Тем самым допустимые пределы изменения на первичные параметры устанавливаются независимо друг от друга. Анализ показал [1], что такой подход приводит к большой методической погрешности, которая нелинейно возрастает в функции числа контролируемых параметров. Кроме того, для не односвязных областей работоспособности известные методы не имеют однозначного решения. Таким образом, актуальна задача разработки метода контроля ТС, обеспечивающего его простоту и высокую достоверность.

Для решения задачи установим связь между первичными X и контролируемыми (измеряемыми) параметрами Z. Сущность предлагаемого подхода сводится к следующему. Известно, что любую динамическую систему с заданной погрешностью можно аппроксимировать системой второго порядка и решить задачу ее идентификации, используя переходную характеристику h(t) или частотную передаточную функцию W(jw). При этом, между параметрами X и Z существует соответствие и области G в пространстве параметров Z соответствует допусковая область F [1].

В процессе параметрического синтеза [2], область G разбивается на подобласти , каждая из которых определяет запас работоспособности . На основании отображения в пространстве параметров Z областям будут соответствовать области . Для аналитического описания границы области воспользуемся аппаратом логических R–функций [1]. При этом область записывается в виде следующего рекуррентного соотношения:

),

где – уравнение j-ой гиперповерхности i-ой подобласти , которое, при необходимости, всегда можно получить, используя методы параметрической идентификации [1]; m и n – размерность соответственно пространства выходных и первичных параметров; S – общее число подобластей ; – параметр преобразования.

Получим уравнение области F. С этой целью для каждой гиперповерхности f_j границы области G, сформируем совокупность N_q граничных точек, равных числу значимых коэффициентов в уравнениях . По этим точкам получим уравнения кривых, составляющих область F. При этом [2]

.

Аналогичным образом определяются границы подобластей . Каждой подобласти соответствует свой запас работоспособности ТС. Так, например, для подобласти для .

Оценка состояния ТС сводится к распознаванию в пространстве параметров Z принадлежности вектора текущего состояния системы той или иной подобласти , где S – число подобластей, для каждой из которых определен запас работоспособности . Задача распознавания решается следующим образом. Если после подстановки полученных в результате контроля значений в последнее уравнение окажется, что , то, ТС находится в работоспособном состоянии и далее проверяется справедливость выполнения неравенств . Если и , то вектор текущего состояния ТС принадлежит подобласти и запас работоспособности ТС равен . Если – система неработоспособна. В этом случае осуществляется параметрическая коррекция настраиваемых параметров ТС [1].

Предлагаемый подход к решению поставленной задачи характеризуется высокой достоверностью и удобством практического использования.

Литература

1. Саушев А.В. Области работоспособности электротехнических систем / А.В. Саушев. – Политехника, 2013. – 412 с.

2. Саушев А.В. Параметрический синтез электротехнических устройств и систем / А.В. Саушев. – СПб: ГУМРФ имени адм. С.О. Макарова, 2013. – 315с.