Бакиров
Ж.Б., Бакиров М.Ж.
Карагандинский
государственный технический университет
СЛУЧАЙНЫЕ НЕСТАЦИОНАРНЫЕ
КОЛЕБАНИЯ
МЕХАНИЧЕСКИХ СИСТЕМ
Случайные
нестационарные колебания в механической системе возникают при действии
случайных нестационарных нагрузок или при стационарных нагрузках на переходных
режимах механической системы. Уравнение вынужденных колебаний линейной системы
с одной степенью свободы с постоянными
коэффициентами имеет вид
![]() , (1)
, (1)
где m – масса колеблющегося элемента; ![]() - случайная сила;
- случайная сила;
ε
– коэффициент затухания колебаний;
ω – частота собственных колебаний.
Начальные
условия возбуждения в общем случае являются случайными величинами. Случайную
нагрузку и начальные данные считаем независимыми.
Решение
уравнения (1) для произвольной правой части имеет вид
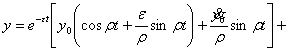
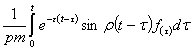 , (2)
, (2)
где у![]() ,
, ![]() - начальные
возбуждения.
- начальные
возбуждения.
Математические
ожидания и корреляционная функция решения
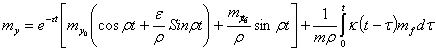 , (3)
, (3)
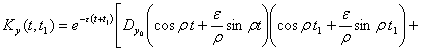
+ 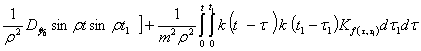 , (4)
, (4)
где ![]() (5)
(5)
Рассмотрим
сначала случай, когда к системе прикладывается гармоническая сила
![]() ,
,
где F –
случайная величина с известными вероятностными характеристиками ![]() и
и ![]() . Начальные условия считаем нулевыми.
. Начальные условия считаем нулевыми.
Решение
в этом случае имеет вид
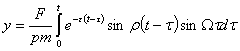 .
.
Производя
замену переменных ![]() , получаем
, получаем
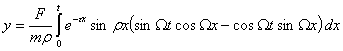 .
.
После
интегрирования находим
![]() ,
,
где 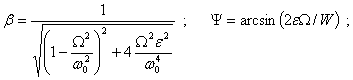
![]()
Математическое
ожидание и корреляционная функция решения будут равны:
![]() ,
,
![]() .
.
Для установившихся колебаний (![]() ) получаем
) получаем
![]() .
.
Теперь
рассмотрим нестационарные колебания, когда нагрузка представляет собой
случайный стационарный процесс типа белого шума. Вероятностные характеристики решения
определяем по формулам (3) и (4) при нулевых начальных условиях. Математическое
ожидание
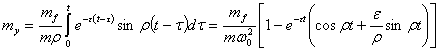 .
.
Корреляционная
функция
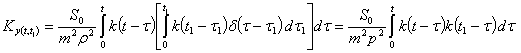 .
.
Подставляя
сюда выражение (5), можно записать
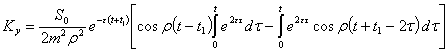 .
.
После
интегрирования получаем
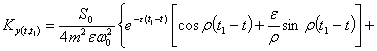
+ 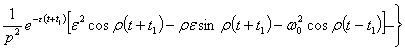 . (6)
. (6)
Отсюда
при t = t![]() определяем дисперсию
определяем дисперсию
![]() . (7)
. (7)
При ![]() получаем
стационарное решение для положительных
получаем
стационарное решение для положительных ![]() . Если решение
распространить на всю действительную ось, то получим
. Если решение
распространить на всю действительную ось, то получим
![]() ,
,
что
совпадает с известным выражением [1].
Аналогично
могут быть найдены вероятностные характеристики решения при других
корреляционных функциях внешнего воздействия. Так, например, для
экспоненциально-коррелированного процесса
![]()
дисперсия
решения при нулевых начальных условиях определяется выражением
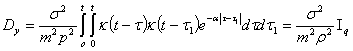 ,
,
где 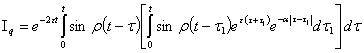 (8)
(8)
Внутренний
интеграл представим в виде суммы двух интегралов, не содержащих модуля
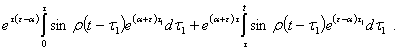
С
учетом того, что
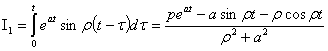 , (9)
, (9)
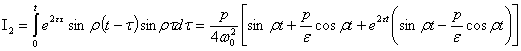 ,
,
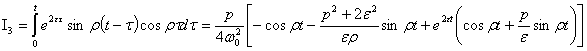 после математических преобразований получаем
после математических преобразований получаем
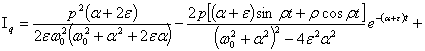
+![]() . (10)
. (10)
При ![]() процесс становится
стационарным, и дисперсия определяется выражением
процесс становится
стационарным, и дисперсия определяется выражением
![]()
и совпадает с выражением,
полученным в работе [2].
Список литературы
1. Болотин В.В. Случайные колебания упругих систем. – М.: Наука, 1979.-336 с.
2. Бакиров Ж.Б. Вероятностные
методы расчета элементов конструкций. - Караганда: КарГТУ, 2001. – 182 с.