технические науки/2. механика

к.т.н. Емельянова О.В, д.т.н. Яцун С.Ф., асп. Попов Н.И., асп. Савин А.И.

ГОУ ВПО "Юго-Западный государственный университет", Курск, Россия

ИССЛЕДОВАНИЕ ВЛИЯНИЯ ДИНАМИЧЕСКИХ ПАРАМЕТРОВ НА ХАРАКТЕР КОЛЕБАНИЙ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ

Введение

Бурное развитие нового класса небольших беспилотных летательных аппаратов (БЛА), способных нести полезную нагрузку в виде контролирующих приборов, видеоаппаратуры, расширило область применения БЛА с целью контроля технического состояния различных объектов, при этом увеличивается роль стабилизации полета. Устойчивость – свойство аппарата восстанавливать без вмешательства оператора кинематические параметры невозмущенного движения и возвращаться к исходному режиму полета после прекращения действия возмущений [2-6]. Поэтому актуальной задачей является исследование динамических явлений, возникающих при внешних периодических воздействиях, а также выбор стратегии управления и параметров регулятора.

Математическая модель БЛА в режиме висения

Рассмотрим режим висения БЛА (квадрокоптера) в плоскости zСy (рис.1). Считаем, что т.С , являющаяся центром квадрокоптера, остаётся неподвижной в режиме висения. С этой точкой связана система координат Схyz, тогда подвижная система координат Сх₁ y₁ z₁ связана с корпусом, который поворачивается относительно оси х на угол φ.

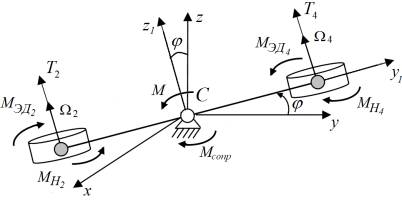
_{Рис.1. Расчётная схема квадрокоптера при для изучения движений}

_{относительно оси Сx}

За обобщенную координату примем угол поворота φ, при этом режим висения квадрокоптера происходит под действием сил Т₂, Т₄, момента сопротивления и момента внешнего периодического воздействия М. Винты приводятся во вращение электродвигателем, генерирующим моменты электродвигателей М_ЭДi , а вращению винтов, с угловыми скоростями w_i, препятствует момент внешних нагрузок М_Hi .

Особый интерес представляет изучение закономерностей движения (колебания) коптера при внешних периодических воздействиях, которые представлены в виде момента M=M₀sin(w₀t), где М₀, w₀ - амплитуда и частота внешнего возмущения

_{Восстанавливающий момент, действующий на корпус со стороны винтовых электроприводов, определяется величиной управляющих напряжений, поступающих из системы автоматического управления на левый и правый электроприводы. Причем уровень напряжений, формируемых усилителем мощности САУ, полностью зависит от принятой стратегии управления.}

Дифференциальные уравнения для двух винтов, которые описывают взаимосвязанные электромагнитные и механические процессы в электромеханической системе приводов винтов квадрокоптера, имеют вид:

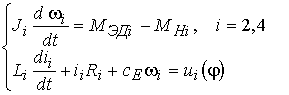, (1)

где L_i, R_i –индуктивность и активное сопротивление обмотки ротора; u_i – управляющее напряжение, i – ток в обмотке электромагнита, w_i, W_i - угловые скорости электродвигателя и пропеллера соответственно; с_Е - коэффициент пропорциональности, называемый постоянной ЭДС двигателя; J_i - приведенный осевой момент инерции.

Момент, создаваемый электродвигателями:

, (2)

где c_Mi - коэффициент пропорциональности момента.

Связь между угловой скоростью электродвигателя w_i и винта Wi:

w_i / W_i =N , (3)

где N– передаточное отношение редуктора.

Момент внешних нагрузок М_Нi будем определять как:

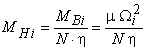, i =2,4. (4)

где М_Вi = - момент сопротивления вращению винта, m - коэффициент нагрузки, приведенный к валу двигателя, h- кпд электропривода.

Движение корпуса квадрокоптера, относительно оси Сх описывается дифференциальным уравнением:

, (5)

где J_x – осевой момент инерции; – главный момент внешних сил относительно оси Ох:

, (6)

где l – расстояние между центром квадрокоптера и центром пропеллера; b_z – аэродинамическая постоянная.

С учетом (6) уравнение (5) будет иметь вид:

(7)

Система дифференциальных уравнений (1), (7) описывает колебания квадрокоптера относительно оси Сх при внешнем периодическом воздействии. В общем случае система является нелинейной и её решение удобно выполнить с помощью численных методов. Однако, сделав некоторые предположения, можно получить аналитическое решение. Пусть электродвигатели, используемые в квадрокоптере обладают небольшой индуктивностью, т.е. , (W₂²» W₂), (W₄²» W₄), , тогда уравнения (1) примут вид:

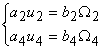, (8)

где: , , , ,

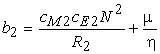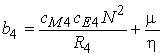Откуда 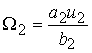, 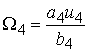. (9)

Обозначим: 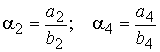, тогда:

. (10)

С учетом (10) уравнение (7) примет вид:

(11)

где .

Пусть управляющее воздействие определяется по следующему алгоритму:

; , (12)

где - постоянное напряжение питания; k- пропорциональный коэффициент.

Тогда уравнение (11) примет вид:

, (13)

или . (14)

Получили уравнение вынужденных колебаний, где , 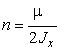– коэффициент демпфирования, 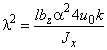– циклическая частота свободных колебаний.

Решение дифференциального уравнения (14) имеет вид [1]:

(15)

Здесь А, В - амплитуды свободных и вынужденных колебаний, g, b - соответственно начальная фаза свободных колебаний и сдвиг фаз вынужденных колебаний по отношению к возмущающей силе.

Амплитуду и сдвиг фаз вынужденных колебаний будем определять по формулам:

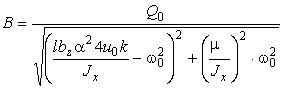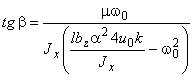, (16)

Исследование динамических параметров на характер колебаний квадрокоптера

Моделирование выполнено с использованием (16) для следующих предельных случаев:

1. Если l << w₀, тогда

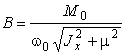, . (17)

2. Если l»w₀, тогда

, . (18)

3. Если l >> w₀, тогда

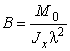, . (19)

Анализ зависимости, представленной на рисунке 2 показал, что при высокочастотных возмущениях (17), в режиме l<<w₀, на величину амплитуды вынужденных колебаний оказывает влияние коэффициент сопротивления m и частота внешнего возмущения w₀, причем с возрастанием последних амплитуда колебаний падает.

При низкочастотных возмущениях (19), в режиме l >> w₀ коэффициент сопротивления m и частота внешнего возмущения w₀ не оказывают воздействия на величину амплитуды вынужденных колебаний, а влияет осевой момент инерции J_x, повышающий стабильность квадрокоптера и частота свободных колебаний l, которая зависит от геометрических размеров квадрокоптера, аэродинамических коэффициентов, свойств электроприводов, управляющего напряжения, передаточного числа редуктора, коэффициента усиления пропорционального регулятора системы автоматического управления.

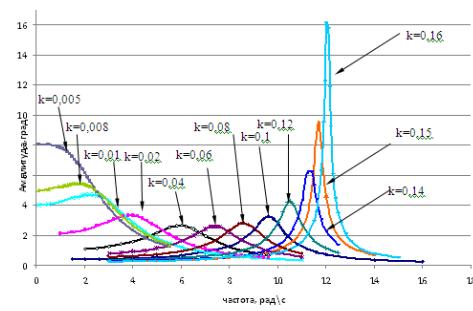
Рис.2. Зависимость амплитуды вынужденных колебаний от величины коэффициента усиления пропорционального регулятора

При частоте возмущения, равной частоте собственных колебаний системы (l»w₀), амплитуда вынужденных колебаний значительно возрастает (18), диссипативные силы уравновешиваются силами инерции при любом значении амплитуды колебаний. Внешняя возмущающая сила оказывается неуравновешенной. Поэтому амплитуда колебаний квадрокоптера, определяемая коэффициентом сопротивления m и частотой свободных колебаний l, в режимах, близких к резонансному, может быть значительной.

Далее изучалось влияние различных коэффициентов сопротивления нагрузки m на величину В амплитуды вынужденных колебаний, которая, в свою очередь, линейно зависит от величины момента внешнего воздействия (рис.3).

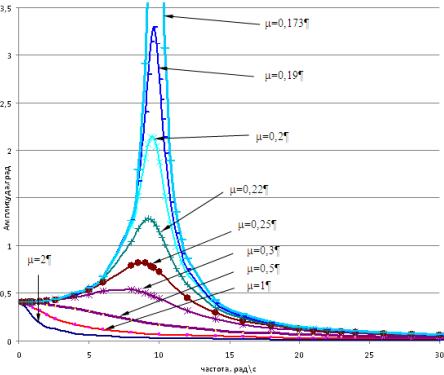
Рис.3. Зависимость амплитуды вынужденных колебаний от частоты внешнего воздействия

График на рисунке 3 показывает, что при уменьшении коэффициента сопротивления нагрузки m < 0,5 максимум амплитуды не наступает. При частоте возмущения, равной частоте собственных колебаний системы, амплитуда вынужденных колебаний возрастает.

Далее исследовалось влияние на амплитуду вынужденных колебаний момента внешнего воздействия при различных коэффициентах сопротивления нагрузки (рис.4) и получена зависимость циклической частоты при различных коэффициентах усиления пропорционального регулятора системы автоматического управления (САУ) (рис.5).

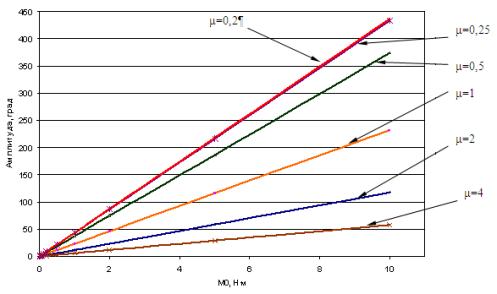
Рис.4. Зависимость амплитуды вынужденных колебаний от величины момента внешнего воздействия

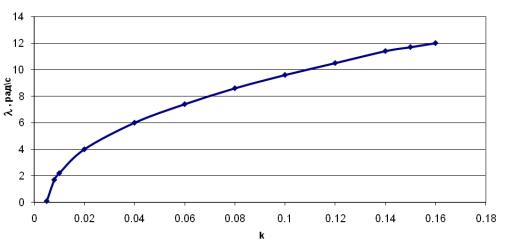
Рис.5. Зависимость циклической частоты колебаний от величины коэффициента усиления пропорционального регулятора

Выводы:

Анализ полученных результатов показал, что амплитуда колебаний квадрокоптера при внешнем периодическом воздействии зависит от частоты внешних возмущений. Имеет место ярко выраженная резонансная зона, в которой происходит значительное увеличение амплитуды, зависящее от диссипативных свойств и конструкции коптера. Величина собственной частоты колебаний коптера зависит от коэффициента усиления пропорционального регулятора, геометрических размеров, величины управляющего напряжения и аэродинамических характеристик винтовых приводов коптера. Установлено, что существует область параметров коэффициента пропорциональности регулятора, обеспечивающих минимальное значение амплитуды вынужденных колебаний.

Литература

1. Бидерман В.Л. Теория механических колебаний: -М.: Высшая школа, 1980. - 408 с.

2. Емельянова О.В., Попов Н. И., Яцун С. Ф. Моделирование движения квадроротационного летающего робота //Актуальные вопросы науки. Материалы VIII Международной научно-практической конференции. - Москва, Спутник+. 2013. -C.6-8.

3. Емельянова О.В., Попов Н. И., Яцун С. Ф. Моделирование движения квадрокоптера в пространстве // Авиакосмические технологии (АКТ-2013). Труды XIV Всероссийской научно-технической конференции и школы молодых ученых, аспирантов и студентов. - Воронеж: ООО Фирма «Элист», 2013. -C.131-138.

4. Яцун С., Ф., Емельянова О.В., Попов Н. И. Изучение движения квадрокоптера в вертикальной плоскости // Актуальные вопросы технических наук (II): материалы международной заоч. науч. конф. - Пермь: Меркурий, 2013.- С.66-69.

5. М.Tahar, K.M.Zemalache, A. Omari Control of under-actuated X4-flyer using indegral Backstepping controller. Przeglad elektrotechniczny (Electrical review), ISSN 0033-2097, R.87 NR 10/2011, pages251-256.

6. А.Bemporad, C.Rocchi Decentralized linear time-varying model predictive control of a formayion of unmanned aerial vehicles/ 50th IEEE Conference on decision and control and European control conference, Orlando, FL, USA,1011, pages 7488-7493.