К.ф.-м.н.
Белов Петр А.
Московский
государственный технический университет им.Н.Э.Баумана, Россия
Существующие модели градиентных теорий упругости и их
обобщение
Теория сред Коссера
(1909год).
Теория сред Коссера [1] является самой старой градиентной
моделью сплошной среды. В общем случае лагранжиан 
теории сред
Коссера может быть представлен в следующем виде:
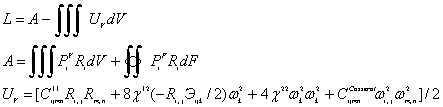
Здесь 
- работа
внешних объёмных 
и поверхностных
сил, 
- объёмная
плотность потенциальной энергии, 
- вектор
перемещений, 
- градиент
вектора перемещений (тензор стесненной дисторсии), 
- псевдовектор
свободных поворотов, которые по определению не могут быть представлены как
ротор перемещений, 
- тензор
Кронекера, 
- псевдотензор
Леви-Чивиты. Тензоры модулей имеют следующую структуру:
,
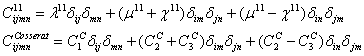- классические
коэффициенты Ламе, 
-
неклассические модули, имеющие ту же размерность, что и классические модули, 
- моментные
модули, по размерности отличающиеся от классических модулей на размерность
квадрата длины.
Эта теория характерна тем, что
каждой точке среды приписывается шесть степеней свободы: три компоненты вектора
перемещений 
и три
компоненты псевдовектора свободных поворотов 
, которые не являются вихрями поля перемещений. Таким
образом, каждая точка такой среды ведет себя как абсолютно твердое тело.
Независимые кинематические переменные 
и 
определяют
кинематическую модель среды Коссера.
Из выражения объемной плотности потенциальной энергии теории сред Коссера следуют формулы Грина, которые определяют силовую модель теории, и уравнения закона Гука для соответствующих силовых факторов:
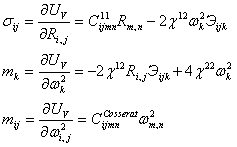
Таким образом, теория сред
Коссера допускает существование в среде следующих внутренних силовых факторов:
несимметричного тензора напряжений 
, псевдовектора объемных моментов 
и псевдотензора
моментных напряжений 
.
Вариационное уравнение теории сред Коссера получено из условия стационарности лагранжиана:
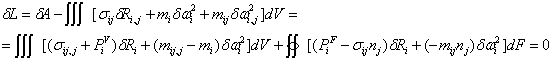
Вариационное уравнение теории сред Коссера в кинематических переменных:
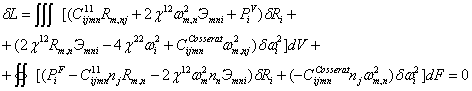
Уравнения Эйлера:
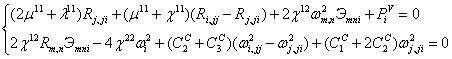
Дивергенция уравнений равновесия моментов дает:
Здесь введено обозначение 
.
Ротор уравнений равновесия сил
при 
дает:
Тогда уравнение равновесия
моментов можно записать относительно 
в
алгебраическом виде:
Подставляя 
в уравнение
равновесия сил, можно получить:
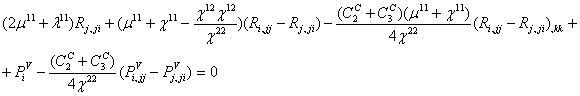Таким образом, теория сред Коссера может быть описана
решением распадающейся системы уравнений относительно вектора перемещений 
и псевдоскаляра
:
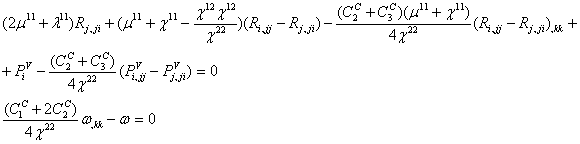При этом краевая задача при 
остается
связанной и содержит шесть граничных условий в каждой неособенной точке
поверхности. Следует обратить внимание на то, что разрешающие уравнения теории
не содержат одной из трех линейных комбинаций «моментных» модулей, а именно: 
. Она фигурирует только в формулировке статических
граничных условий на «моментные» напряжения.
Теория сред Джеремилло
(1929год).
Теория сред Джеремилло [2] также является давно известной,
но незаслуженно забытой, градиентной моделью сплошной среды. В общем случае
лагранжиан 
теории сред
Джеремилло может быть представлен в следующем виде:
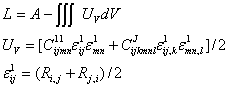
Из факта существования плотности потенциальной энергии следует, что тензоры модулей обладают следующим свойством симметрии:
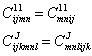
Кроме того, так как тензор шестого ранга 
симметричен при
перестановке индексов внутри пар 
и 
, антисимметричные по этим индексам компоненты тензора
модулей 
не войдут в
выражение потенциальной энергии 
и их можно без
ущерба для общности положить равными нулю. Отсюда:
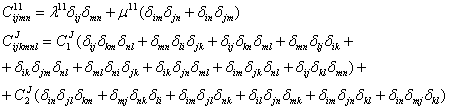
Отметим, что кинематическая
модель теории сред Джеремилло является классической и определяется независимыми
кинематическими переменными 
.
Из выражения объемной плотности потенциальной энергии следуют формулы Грина, которые определяют силовую модель теории, и дают уравнения закона Гука для соответствующих силовых факторов:
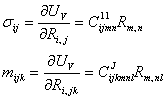
Таким образом, теория сред
Джеремилло допускает существование в среде следующих внутренних силовых
факторов: симметричного тензора напряжений 
и тензора
моментных напряжений 
.
Вариационное уравнение теории сред Джеремилло получено из условия стационарности лагранжиана:
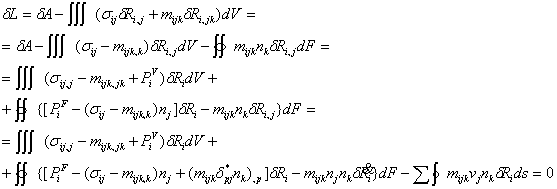
Здесь точкой над переменной обозначена нормальная к
поверхности производная 
. 
- «плоский» тензор Кронекера, 
- орт
криволинейной ортогональной системы координат, связанной с ребром
кусочно-гладкой поверхности, ограничивающей тело 
, 
- орт
касательной к ребру, 
- «реберные»
силы.
В перемещениях вариационное уравнение теории сред Джеремилло имеет вид:
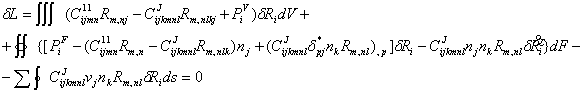
Таким образом, уравнения Эйлера теории дают систему трех уравнений четвертого порядка с шестью граничными условиями в каждой неособенной точке поверхности.
Характерной особенностью теории является наличие условий на ребрах:
Условия на ребрах можно трактовать как условия непрерывности
(при переходе по поверхности через ребро) вектора перемещений 
и вектора
«реберных» сил 
.
Теория сред Аэро-Кувшинского
(моментная теория упругости, 1960год).
Теория сред Аэро-Кувшинского [3] является градиентной
моделью сплошной среды с классической кинематикой. В отличие от теории сред
Коссера в ней за дополнительные параметры состояния выбраны не свободные
повороты 
, а вихри перемещений 
. Доказано [4], что если постулировать
пропорциональность свободных поворотов вихрям перемещений (гипотезу
Аэро-Кувшинского), теория сред Аэро-Кувшинского является следствием теории
Коссера. С другой стороны, теория сред Аэро-Кувшинского может рассматриваться
как некая альтернатива теории Джеремилло. Действительно, если градиентная часть
потенциальной энергии в теории Джеремилло содержит только градиенты
симметричной части градиента перемещений (тензор стесненных деформаций), то
градиентная часть в теории Аэро-Кувшинского содержит только градиенты
антисимметричной части градиента перемещений (тензор стесненных поворотов или
псевдовектор стесненных поворотов). Лагранжиан 
теории сред
Аэро-Кувшинского может быть представлен в следующем виде:
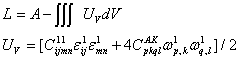
Из факта существования плотности потенциальной энергии следует, что тензоры модулей обладают следующим свойством симметрии:
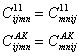
Причем при формулировке теории заранее требовалась такая симметрия тензора «моментных» модулей, чтобы выражение объёмной плотности потенциальной энергии содержало только градиенты вихрей перемещений.
Действительно, при выбранной структуре тензора 
, выражение объёмной плотности потенциальной энергии
приводится к виду:
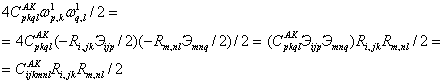
Кроме того, так как псевдотензор второго ранга 
имеет нулевой
след, свертки 
и 
, содержащие один и тот же «моментный» модуль, не
войдут в выражение потенциальной энергии 
, и его можно без ущерба для общности положить равными
нулю. Отсюда:
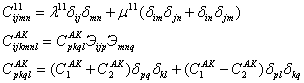
Отметим, что кинематическая
модель теории сред Аэро-Кувшинского является классической и определяется
независимыми кинематическими переменными 
.
Из выражения объемной плотности потенциальной энергии следуют формулы Грина, которые определяют силовую модель теории, и дают уравнения закона Гука для соответствующих силовых факторов:
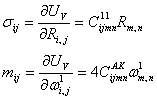
Таким образом, теория сред
Аэро-Кувшинского допускает существование в среде следующих внутренних силовых
факторов: симметричного тензора напряжений 
и псевдотензора
моментных напряжений 
.
Вариационное уравнение теории сред Аэро-Кувшинского получено из условия стационарности лагранжиана:
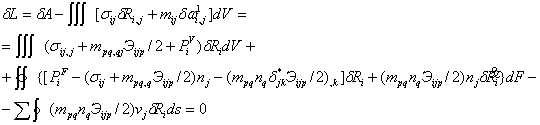
Здесь точкой над переменной обозначена нормальная к
поверхности производная 
. 
- «плоский» тензор Кронекера, 
- орт
криволинейной ортогональной системы координат, связанной с ребром
кусочно-гладкой поверхности, ограничивающей тело 
, 
- орт касательной
к ребру, 
- «реберные»
силы.
В кинематических переменных (перемещениях) вариационное уравнение имеет вид:
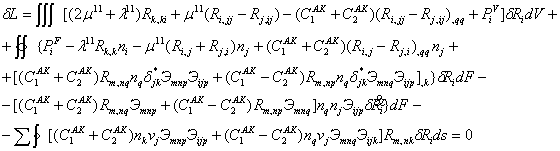
Таким образом, формулировка теории сред Аэро-Кувшинского
определяется тремя дифференциальными уравнениями повышенного (четвертого)
порядка специального вида. Специальный вид определен тем, что из двух векторов,
которые возможно построить из вектора перемещений путем четырехкратного
дифференцирования, в уравнениях фигурирует только одна их линейная комбинация.
Спектр краевых задач определен пятью граничными условиями в каждой неособенной
точке поверхности. Действительно, при выделении из 
её проекции по
нормали к поверхности, можно убедиться, что соответствующий «статический» множитель
тождественно равен нулю за счет свертки симметричного 
и
антисимметричного 
тензоров по
индексам 
:
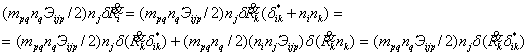
Характерной особенностью теории является наличие условий на ребрах:
Условия на ребрах можно трактовать как условия непрерывности
(при переходе по поверхности через ребро) вектора перемещений 
и вектора
«реберных» сил 
.
Теория сред
Миндлина (1964год).
Теория сред Миндлина [5] является наиболее общей
общепризнанной градиентной моделью сплошной среды. В отличие от теории Коссера
в ней учитываются не только антисимметичная часть тензора свободной дисторсии
(свободные повороты), а все компоненты тензора свободной дисторсии 
. Так же не делается никаких предположений о структуре
тензора моментных модулей. Лагранжиан 
теории Миндлина
может быть представлен в следующем виде:
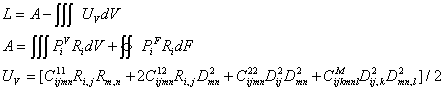
Из факта существования плотности потенциальной энергии следует, что тензоры модулей обладают следующим свойством симметрии:
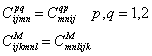
Отсюда:
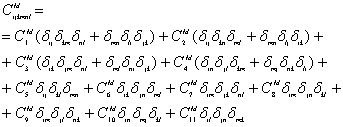
Отметим, что кинематическая
модель теории сред Миндлина является наиболее сложной из всех общепризнанных
теорий и определяется независимыми кинематическими переменными 
и 
. В отличие от теории Коссера, каждая точка среды
Миндлина ведет себя не как абсолютно твердое тело, а как упругое тело.
Соответственно, независимыми степенями свободы являются не только вектор
перемещений 
и псевдовектор
свободных поворотов 
(что
свойственно средам Коссера), но и тензор свободных (несовместных) деформаций 
.
Из выражения объемной плотности
потенциальной энергии 
следуют формулы
Грина, которые определяют силовую модель теории, и дают уравнения закона Гука
для соответствующих силовых факторов:
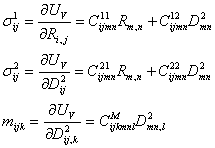
Таким образом, теория сред
Миндлина допускает существование в среде следующих внутренних силовых факторов:
в общем случае несимметричных тензоров напряжений 
и 
второго ранга и
тензора моментных напряжений 
третьего ранга.
Вариационное уравнение теории сред Миндлина получено из условия стационарности лагранжиана:
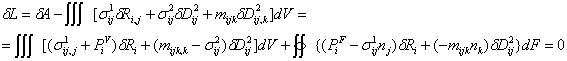
В кинематических переменных (перемещениях и свободных дисторсиях) вариационное уравнение имеет вид:
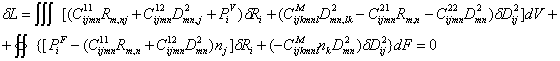
Таким образом, формулировка теории сред Миндлина определяется двенадцатью дифференциальными уравнениями второго порядка. Спектр краевых задач определен двенадцатью граничными условиями в каждой неособенной точке поверхности.
Теория сред Тупина [6] является одной из наиболее популярных
градиентных моделей сплошной среды. В отличие от теории Аэро-Кувшинского и
теории Джеремилло в ней не делается никаких предположений о структуре тензора
моментных модулей. Лагранжиан 
теории Тупина
может быть представлен в следующем виде:
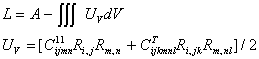
Из факта существования плотности потенциальной энергии следует, что тензоры модулей обладают следующим свойством симметрии:
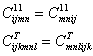
Кроме того, в силу симметрии тензоров стесненных кривизн 
и 
относительно
перестановок индексов 
и 
, тензор Тупина 
так же должен
быть симметричным при перестановках в этих парах индексов. Отсюда следует:
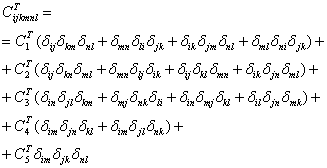
Отметим, что кинематическая
модель теории сред Тупина, так же, как и в теориях Аэро-Кувшинского и
Джеремилло, является классической и определяется независимыми кинематическими
переменными 
.
Из выражения объемной плотности
потенциальной энергии 
следуют формулы
Грина, которые определяют силовую модель теории, и дают уравнения закона Гука
для соответствующих силовых факторов:
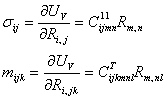
Таким образом, теория сред
Тупина допускает существование в среде следующих внутренних силовых факторов:
симметричного тензора напряжений 
второго ранга и
тензора моментных напряжений 
третьего ранга.
Вариационное уравнение теории сред Тупина получено из условия стационарности лагранжиана:
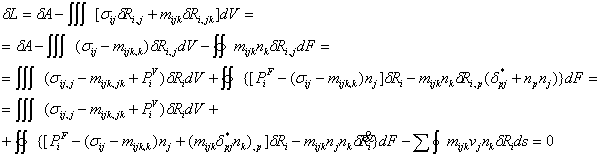
Отметим, что формулировки теорий Тупина, Аэро-Кувшинского и
Джеремилло в «напряжениях» совпадают, а в перемещениях отличаются в силу
различной структуры тензоров моментных модулей 
, 
и,
соответственно, 
.
В кинематических переменных (перемещениях) вариационное уравнение имеет вид:
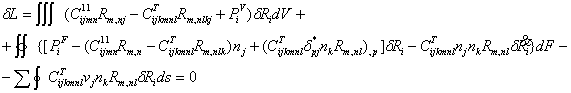
Таким образом, формулировка теории сред Тупина определяется тремя дифференциальными уравнениями четвертого порядка. Спектр краевых задач определен шестью граничными условиями в каждой неособенной точке поверхности.
Общей характерной особенностью теорий Тупина, Аэро-Кувшинского и Джеремилло является наличие условий на ребрах.
«Простейшая» теория
сред с сохраняющимися дислокациями (2009г.).
«Простейший» вариант теории сред с сохраняющимися
дислокациями (ССД) сформулирован в предположении существования в среде полей сохраняющихся
дислокаций [7]. Эта модель характеризуется тем, что градиентная часть
потенциальной энергии является квадратичной формой компонентов псевдотензора 
плотности
дислокаций Де Вита. Наличие ненулевого псевдотензора плотности дислокаций
определяет существование в среде полей дислокаций. Тождественное равенство нулю
дивергенции этого псевдотензора определяет локальный закон сохранения полей
дислокаций. Таким образом, в данной модели поля дислокаций не могут рождаться
или исчезать, а только локально менять свою концентрацию. Лагранжиан 
теории может
быть представлен в следующем виде:
Тензор моментных модулей 
имеет следующую
структуру:
Отметим, что кинематическая
модель теории ССД, совпадает с кинематической моделью теории Миндлина и
определяется независимыми кинематическими переменными 
и 
.
Из выражения объемной плотности
потенциальной энергии 
следуют формулы
Грина, которые определяют силовую модель теории, и дают уравнения закона Гука
для соответствующих силовых факторов:
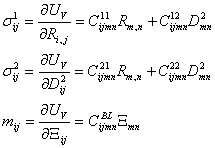
Таким образом, теория ССД
допускает существование в среде следующих внутренних силовых факторов: в общем
случае несимметричных тензоров напряжений 
и 
второго ранга и
псевдотензора моментных напряжений 
второго ранга.
Вариационное уравнение теории ССД получено из условия стационарности лагранжиана:
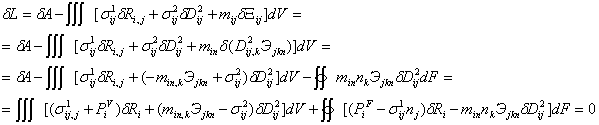
В кинематических переменных (перемещениях и свободных дисторсиях) вариационное уравнение имеет вид:
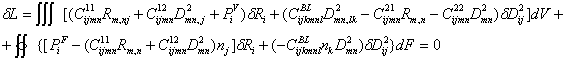
Здесь 
.
Таким образом, формулировка теории ССД определяется двенадцатью
дифференциальными уравнениями второго порядка специального вида. Специальный
вид определен тем, что дивергенция уравнений равновесия моментов приводит к
локальному закону сохранения 
. Следовательно, общий дифференциальный порядок будет ниже,
чем в теории Миндлина. Спектр краевых задач определен девятью граничными
условиями в каждой неособенной точке поверхности. В этом не трудно убедиться,
обратив внимание на то, что в возможной работе моментных силовых факторов на
поверхности содержится только шесть из девяти слагаемых:
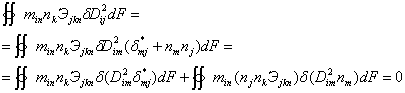
Действительно, второй интеграл тождественно равен нулю в
силу свертки симметричного тензора 
с антисимметричным
псевдотензором 
. Таким образом, в формулировках краевых задач «простейшей»
теории ССД фигурируют только шесть неклассических граничных условий (в
дополнение к трем классическим).
Сравнительный анализ существующих градиентных теорий.
Существующие градиентные теории можно разделить на две группы.
В первую входят теории Тупина, Аэро-Кувшинского и Джеремилло.
Во вторую – теории Миндлина, Коссера и сред с сохраняющимися дислокациями.
Первая группа характеризуется тем, что все теории этой группы построены на основе классической кинематической модели – каждой точке среды эти теории приписывают три степени свободы – компоненты вектора перемещений. Соответственно, и уравнений равновесия в этих теориях три.
Вторая группа, в противоположность первой, характеризуется тем, что теории этой группы построены на основе неклассической кинематической модели. Каждой точке среды эти теории приписывают дополнительные степени свободы: в теории Коссера – это три компоненты псевдовектора свободных поворотов, а в теории Миндлина и в теории ССД - три компоненты псевдовектора свободных поворотов и шесть компонент тензора свободных деформаций. Соответственно, и уравнений равновесия в этих теориях больше: в теории Коссера – шесть, в теориях Миндлина и ССД – двенадцать.
Теория Тупина является наиболее общей теорией первой группы и содержит теории Аэро-Кувшинского и Джеремилло как свои строгие частные случаи.
Теория Миндлина является наиболее общей теорией второй группы и содержит теорию Коссера и теорию ССД как свои строгие частные случаи.
Таким образом, имеется возможность проводить сравнительный анализ групп, сравнивая теории Тупина и Миндлина, как максимально общих теорий в своих группах.
Можно записать лагранжианы обеих теорий в унифицированном
виде, записав потенциальные энергии в терминах стесненных 
и свободных 
дисторсий:
В теории Тупина:
В теории Миндлина:
Такой унифицированный вид позволяет придать потенциальной энергии дисторсий в обеих теориях общий универсальный вид:
В то же время потенциальные энергии кривизн нельзя записать подобным же образом. Если все-таки сделать это:
Получится обобщение теорий Миндлина и Тупина одновременно (за счет появления слагаемых, билинейных по кривизнам разных сортов, связанных со стесненными и свободными дисторсиями):
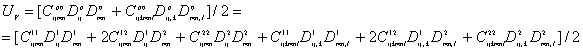
Если лишить такую обобщенную среду части своих механических
свойств, положив нулю тензоры 
, получим теорию Тупина, как строгий частный случай,
положив нулю тензоры 
, получим теорию Миндлина, как другой строгий частный
случай.
Таким образом, здесь постулировано, а в [8] независимо построено, обобщение всех известных градиентных теорий.
Литература.
1. Cosserat
E., Cosserat F., «Theorie des Cops Deformables», 1909, Paris, Hermann.
2. Jaramillo T.J. «A generalization of the energy function of elasticity theory», Dissertation, Department of Mathematics, University of Chicago, 1929.
3. Аэро Э.Л., Кувшинский Е.В. «Основные уравнения теории упругости сред с вращательным взаимодействием частиц», 1960, ФТТ, т. 2, вып. 7, 1399-1409.
4. Лурье С.А., Белов П.А. «Теория сред с сохраняющимися
дислокациями. Частные случаи: среды Коссера и Аэро-Кувшинского, пористые среды,
среды с «двойникованием»», Сб. трудов конференции «Современные проблемы
механики гетерогенных сред», 2005, Изд. ИРПИМ РАН, стр. 235-268.
5. Mindlin
R.D. «Micro-structure in linear elasticity», «Archive of Rational Mechanics and
Analysis», 1964, №1, p. 51-78.
6. Toupin
R.A. «Elastic materials with couple-stresses», 1962, Arch. Ration. Mech. And Analysis.
7. Белов П.А., Лурье С.А. «Континуальная модель микрогетерогенных сред», ПММ, 2009, т.73, №5, стр. 833-848.
8. Белов П.А.
«Теория сред с сохраняющимися дислокациями. Обобщение модели Миндлина», Композиты и наноструктуры.
2011. № 1.
С. 24-38.