Технические науки/3. Отраслевое машиностроение

Аспирант Исмайлова Е.Ю., д.т.н. Демин Ф.И.

Самарский государственный аэрокосмический университет имени академика С.П. Королева (национальный исследовательский университет), Россия

Определение геометрической погрешности многокоординатного шлифовального станка с ЧПУ при обработке деталей газотурбинных двигателей

Современный этап развития авиационного и космического двигателестроения характеризуется совершенствованием параметров двигателей, повышением требований к надежности при эксплуатации, увеличением сложности конструкции двигателей. По мере развития и совершенствования газотурбинных двигателей (ГТД) возрастают требования к обеспечению показателей точности входящих в сборочные единицы деталей. Сложность формы шлифуемых заготовок и требования к высокой точности взаимного расположения стыковых поверхностей деталей (бандажных полок относительно замка, профилей левой и правой части замка относительно друг друга и относительно оси замка, а также ряд других требований) целесообразно обеспечивать обработкой на многокоординатных шлифовальных станках с ЧПУ [1, с.23].

Таким образом, актуальными являются вопросы обеспечения точности обработки на многокоординатных шлифовальных станках с ЧПУ. Соответственно, целью данной работы является анализ сущности проявления пространственных погрешностей на основе исследования размерных связей, а также определение поля рассеивания суммарной погрешности при многокоординатном управлении шлифовальным станком с ЧПУ.

Существующие методы расчета точности, применяемые в машиностроении, являются линейными или приведенными к линейным. Рассматриваемый в данной статье способ оценки точности предусматривает векторную форму размерных связей, которая позволяет учитывать все элементы неразрывной размерной цепи.

Известно, что на точность формообразования при механической обработке заготовок оказывают влияние систематические постоянные, систематические закономерно изменяющиеся и случайные производственные погрешности. Погрешности характеризуются как линейными величинами, так и угловыми, определяющими направление действия фактора, т.е. могут быть представлены в векторной форме [2, с.87-125]. Последовательность и неразрывность размерных связей при переходе от одной координатной плоскости к другой представлена схемой на рис.1.

Полученная схема отражает всю совокупность линейных и угловых связей обрабатываемых размеров и погрешностей, действующих при обработке: при управлении по двум координатам в плоскости ZX, при повороте А стола с заготовкой на угол φ_x, при вертикальном перемещении вдоль оси Y, повороте В стола на угол φ_y, повороте С на угол φ_z.

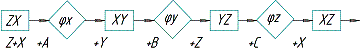
Рисунок 1. Схема размерных связей при многокоординатном управлении на шлифовальном станке с ЧПУ

Для исследования размерных связей на практике применяется теория размерных цепей. Сложная объемная обработка приводит к образованию пространственных размерных цепей. На рис.2 представлена схема формирования пространственной размерной цепи при обработке на шлифовальном станке с ЧПУ, имеющим 5 управляемых координат.

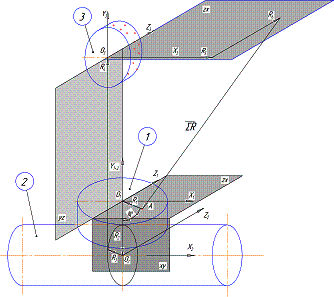
Рисунок 2. Схема формирования пространственной размерной цепи

при управлении обработкой по 5 координатам на шлифовальном станке с ЧПУ

Звеньями представленной размерной цепи являются погрешности, связанные с геометрической точностью станка. Так, вектор ₁ выражает суммарную погрешность, связанную с геометрической неточностью стола поз.1, в горизонтальной плоскости Z0X. После поворота (координата А) стола поз.2 на угол φ_x, с вектором ₁ суммируется вектор ₂, выражающий ошибку выполнения вращения стола. Суммарная погрешность в координатной плоскости X0Y на схеме выражена вектором ₃. При вертикальном перемещении шлифовального круга (координата Y) возникают ошибки позиционирования, графически выраженные вектором ₄ в координатной плоскости Y0Z. Звенья размерной цепи ₅ и ₆ отражают погрешности продольных и поперечных перемещений базовой точки инструментального блока (координаты X и Z) в плоскости Х0Z.

Из схемы видно, что графически пространственные погрешности образуют замкнутый пространственный многоугольник, выражающий пространственную векторную цепь. Замыкающим звеном цепи является суммарный вектор Σ_, отражающий всю совокупность погрешностей, влияющих на геометрическую точность многокоординатного шлифовального станка с ЧПУ.

Для нахождения вероятностных характеристик суммарного пространственного вектора на практике можно произвести моделирование процесса и, используя вероятно-статистические методы, определить фактическое поле рассеивания суммарной пространственной погрешности.

Далее представлен результат имитационно-статистического моделирования пространственной погрешности шлифовального станка с ЧПУ Blohm Profimat MC610, полученный в СГАУ с помощью программного обеспечения «Вектор».

Для расчета геометрической точности станка построена размерная цепь (рис.3, а), звеньями которой являются векторы №1…7.

а б

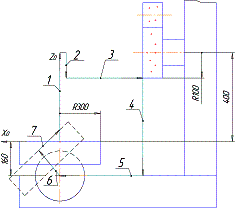
Рисунок 3. Схема размерной цепи шлифовального станка с ЧПУ Blohm Profimat MC610:

а – основа расчета; б – графическое отображение программой

Вектор 1 учитывает отклонение расположения оси шлифовального круга от номинального; вектор 2 учитывает износ шлифовального круга; вектор 3 - погрешность настройки положения режущего инструмента относительно базовой точки стола станка; вектор 4 - погрешность расположения инструмента относительно оси поворота стола в направлении оси Z; вектор 5 - погрешность расположения инструмента относительно оси поворота стола в направлении оси X; вектор 6 - угловую погрешность при повороте стола на угол βz; вектор 7 выражает угловую погрешность возврата базовой точки стола в нулевую позицию. Векторная размерная цепь рассмотрена в плоскости ZX. Для упрощения расчета погрешности, действующие в направлении оси Y, приняты равными нулю. Рассматриваемая размерная цепь введена в качестве исходных данных в программу «Вектор» (рис.3, б).

Численные значения звеньев размерной цепи приведены в таблице 2.

Таблица 2 – Исходные данные для расчета точности станка

Параметры вектора	X	Y	Z	||	φ	T	β	α	μ1	μ2	Примеча-ние
№№
	0	0						αy=0			Плоскость XY
		0	0					αz=0			Плоскость YZ
1	0 ±0,002		400 ±0,002				0				Плоскость ZX
2	0 ±0,002		-100 ±0,002				0				Плоскость ZX
3	-300 ±0,002		0 ±0,002				0				Плоскость ZX
4	0 ±0,002		-460 ±0,002				0				Плоскость ZX
5	300 ±0,002		0 ±0,002				0				Плоскость ZX
6				160 ±0,002	45º ±1̎		45º ±1̎				Плоскость ZX
7				160 ±0,002	315 ±1̎						Плоскость ZX

Расчет поля рассеивания геометрической погрешности станка выполнен программой для различного числа случайных точек n. Результаты расчета для n=100, n=200, n=500 представлены в таблице 3.

Таблица 3 – Результаты расчета поля рассеивания геометрической погрешности станка программой «Вектор»

Количество случайных точек n	Предельные значения погрешностей			Величина поля рассеивания ω
	по координате	max	min
n=100	X	0,006	-0,001	ωx=0,007
	Y	0	0	ωy= 0
	Z	126,277	126,271	ωz=0,006
n=200	X	0,007	-0,003	ωx=0,010
	Z	126,277	126,271	ωz=0,006
n=500	X	0,005	-0,003	ωx=0,008
	Z	126,279	126,268	ωz=0,011

На рис. 4, а представлен вариант отображения программой результата расчета векторной размерной цепи, а на рис. 4, б – облако рассеивания случайных точек при n=500.

а б

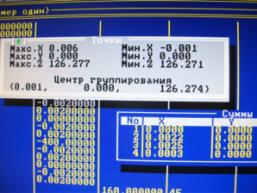
Рисунок 4. Отображение программным обеспечением «Вектор» результата

расчета векторной размерной цепи

Таким образом, с помощью метода имитационно-статистического моделирования с использованием программного обеспечения «Вектор» выполнен расчет геометрической точности многокоординатного шлифовального станка с ЧПУ. В данной работе произведена оценка одной составляющей погрешности обработки Δ_о, зависящей от точности оборудования.

Предложенная методика расчета позволяет: учесть линейные и угловые размерные связи при многокоординатном управлении; применить для расчета композиционный закон распределения погрешностей; установить значение μ- соотношение случайной и равновероятной составляющей в композиции законов распределения погрешностей; вводить в размерную цепь составляющие звенья, учитывающие погрешности приспособления, погрешности установки заготовки и других элементов технологической системы.

Литература:

1. Демин Ф.И., Проничев Н.Д., Шитарев И.Л. Технология изготовления основных деталей газотурбинных двигателей: учеб. Пособие. – М.: Машиностроение, 2002. – 328 с.

2. Демин Ф.И. Расчеты точности геометрических систем и моделей//Основы теории точности машин и приборов. РАН, институт проблем машиноведения.- СПб.: Наука, 1993. – С. 87–125.