К.ф.- м. н. Раевская Л.Т.

Уральский государственный лесотехнический университет, г. Екатеринбург

ОПРЕДЕЛЕНИЕ РАЦИОНАЛЬНЫХ КОНСТРУКТИВНЫХ ПАРАМЕТРОВ ПОРШНЯ ПНЕВМОМОТОРА

В данной работе проведено вычисление рациональных параметров опасного сечения поршня аксиально-поршневого пневмомотора серии ДАР в области паза. Цель этого исследования – определение таких параметров, которые привели бы к уменьшению изгибных деформаций стенок поршня.

Преимущества аксиально-поршневых пневмодвигателей типа ДАР: малые габариты на единицу мощности, пригодность для работы в тяжелых эксплуатационных условиях (повышенные температуры, пыль, влажность, вибрация), высокая безопасность работы позволяют использовать их в качестве приводов. Эти двигатели по сравнению с радиально-поршневыми той же мощности имеют в полтора-два раза меньшие габариты и массу [1]. Поршни двигателей серии ДАР расположены параллельно оси ротора. На торцевые поверхности прикладывается поочередно давление из газораспределительной магистрали. Около 80% отказов в процессе эксплуатации двигателей серии ДАР происходят из-за трещин в стенках поршня, появление которых связано с внецентренным растяжением – сжатием. Трещины при эксплуатации появляются в углах паза. Конечно-элементная модель поршня пневмомотора ДАР-14М, построенная с помощью программного комплекса ANSYS, представлена на рисунке 1. В центре поршня находится паз, через который при эксплуатации движется ротор. На рисунке 1 видны также отверстия под палец с роликом, обкатывающим ротор. Между опорами под палец – ребро жесткости для уменьшения деформации изгиба. Ребро жесткости имеет вид трапеции (рис.2).

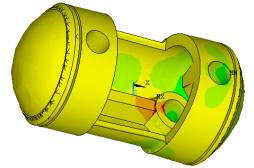
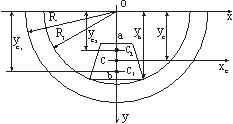
Рис.1. Поле напряжений в теле поршня Рис. 2. Опасное сечение поршня

В предыдущей работе по оптимизации ребра жесткости поршня [2] были приведены результаты аналитического расчета размеров ребра жесткости без учета тела поршня. Полученные результаты показали сильную зависимость величины нормального максимального напряжения в различных направлениях от параметров ребра жесткости. В связи с необходимостью уточнения изложенных в статье [2] результатов в данной работе проведен расчет параметров с учетом всего сечения поршня в области паза. Цель этого исследования – подбор такого сечения ребра жесткости при сохранении его массы и высоты, которое привело бы к уменьшению изгибных деформаций стенок поршня. На рисунке 2 показано сечение поршня в той его части, где появляется наибольшая деформация изгиба в процессе эксплуатации. Сечение можно представить, как составное из трапеции, сегмента и полукольца. Приняты следующие обозначения: С₁ – центр тяжести трапеции, С₂ – центр тяжести полукольца (центр тяжести сегмента не показан на рис.2), С – центр тяжести составного сечения, О – точка, через которую проходит линия действия внешней силы Р (эта линия перпендикулярна плоскости сечения), Yc₁– координата центра тяжести трапеции, Yc₂ – координата центра тяжести полукольца, Yс – координата центра тяжести составного сечения, Y_b – расстояние от нижнего основания трапеции до начала отсчета, Х_c – центральная ось. Кроме того, приняты следующие обозначения: a – размер верхнего основания трапеции, b – нижнего, высота трапеции – h; R, R₁ – больший и меньший радиусы полукольца, соответственно. Пусть S₁, S₂ , S₃ – площади трапеции, полукольца и сегмента, соответственно.

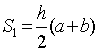
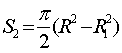
(1)

В данной работе пренебрегали площадью сегмента в силу малости по сравнению с остальными площадями. Вместе с тем, сегмент объединял отдельные площади в единое целое - сечение поршня. С целью увязать (в отсутствие площади сегмента) точки окружности радиуса R₁ и концы отрезка b составлены необходимые соотношения

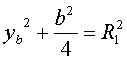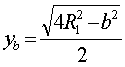,,. (2)

Высота ребра жесткости конструктивно не должна превышать 15 мм длясвободного движения ротора в двигателе ДАР-14М. Получаем для координаты центра тяжести составного сечения следующее соотношение 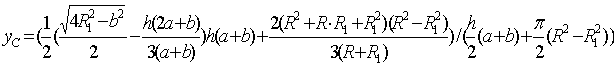(3)

Воспользуемся известными соотношениями для моментов инерции трапеции J₁ и полукольца J₂ относительно своих центров тяжести:

J₁ = (h³/36)(a²+4ab+b²)/(a + b)

J₂ = 0.110R⁴-0.110R₁⁴-0.283R²R₁²(R - R₁)/(R + R₁),

и с учетом соотношений (2), (3) получим выражение для момента инерции полного сечения относительно общего центра тяжести

J_X = J₁ + S₁(Yc₁ - Yc)² + J₂ + S₂(- Yc₂ + Yc)² ;

Вычисленные с учетом (3) моменты инерции сечения относительно центральных осей подставлялись в формулу для нормального максимального напряжения при

внецентренном растяжении-сжатии.

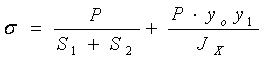, (4)

где Р – величина результирующей силы, приложенной к сечению, линия действия которой проходит через точку О (рис.2); y_o- координата точки приложения результирующей силы, y₁- координата самой удаленной от нейтральной линии точки сечения. Нейтральная линия расположена между центрами тяжестей частей составного сечения и проходит ниже центральной оси. Далее ввиду громоздкости выражения для нормального напряжения расчет проводился с помощью программы MAPLE 9.5. Прежде всего, было установлено, что нормальное максимальное напряжение не имеет экстремума в заданной области изменения параметров (рис.3) и, следовательно, надо минимизировать функцию. Для проведения минимизации функции σ(a, b) в качестве ограничения была выбрана связь между параметрами в виде a + b – 2S/h=0.

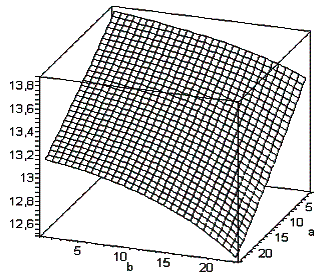
Рис 3. Зависимость σ от параметров а, b

Это ограничение можно использовать для любого типа двигателей ДАР. В частности, для пневмомотора ДАР-14М эта величина равна 2S/h=24 мм. Кроме того, гораздо больший вклад в напряжение σ дает второе слагаемое в формуле (4), которое появляется из-за деформации внецентренного растяжения - сжатия. Из рисунка 3 видно, что увеличение параметра a (соответственно, в силу существующего ограничения уменьшение b) приводит к уменьшению напряжения. Это объясняется тем, что при условии постоянства площади сечения трапеции (ограничения на параметры) рост параметра a приближает центр тяжести сечения к точке приложения силы P, тем самым, уменьшая плечо силы. Если параметры ребра жесткости выбрать, например, а=20мм, b=4мм, то уменьшение напряжения вдоль оси поршня составит 4-6%. С целью проверки этого результата была построена расчетная модель, у которой были закреплены точки на внутренней поверхности отверстия под палец с роликом с той стороны, где прикладывается внешняя нагрузка в виде давления на торец поршня. Статический расчет показал, что для двух наборов параметров: a = 8 мм, b = 16 мм (существующие в настоящее время параметры ребра жесткости); a = 20 мм, b = 4 мм, действительно уменьшение нормального максимального напряжения вдоль оси поршня составляло 4% , что подтверждает точность теоретического расчета. Вместе с тем, следует отметить, что в программном комплексе ANSYS были вычислены напряжения во всех узлах конечных элементов. И для напряжений вдоль оси У, перпендикулярной к оси поршня в некоторых узлах уменьшение напряжения достигало 17-20 %. Таким образом, можно предполагать, что существуют более рациональные параметры ребра жесткости, которые позволяют уменьшить изгибное напряжение и как следствие – отказы поршня.

Библиографический список

1. Яшин А.Н., Анкудинов Д.Т. Машины и оборудование для горнодобывающей промышленности и строительства. Уральский лесотехнический институт, Екатеринбург, с.77, 1992г.

2. Раевская Л.Т. Оптимизация ребра жесткости поршня пневмомотора /Л.Т.Раевская/ Известия вузов. Горный журнал, №6, 2008.- С. 90-94.