Д.т.н. Сулейменов О.А.

Таразский государственный университет, Казахстан

ЗАВИСИМОСТЬ ПОСТОЯННОЙ ВРЕМЕНИ ЗАРЯДКИ ОТ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ МИНЕРАЛОВ

Изучение процесса зарядки частиц, находящихся на осадительном электроде, можно производить с учетом ранее разработанных положении /1-3/, заключающихся в одновременном учете диэлектрической проницаемости и проводимости частиц в форме полуэллипсоида.

При исследовании индукционной зарядки частиц задача представлена в следующем виде: на заряженную проводящую плоскость, создающую однородное поле, помещается незаряженное тело, имеющее форму половины трехосного эллипсоида, причем большая полуось расположена перпендикулярно к проводящей плоскости. Диэлектрическая проницаемость тела ε₁ и среды ε₂, объемная проводимость тела γ₁ и среды γ₂ заданы.

Постоянная времени переходного процесса, согласно / 2,3 /, запишется в следующем виде:

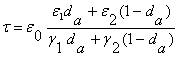( 1 )

где d_a - коэффициент деполяризации.

Воздушная среда характеризуется относительной диэлектрической проницаемостью равной единице. После ионизации при обычных условиях, удельная объемная проводимость воздуха приблизительно равна 0,25×10^-9Ом^-1×м^-1 /3/. Поэтому постоянная времени зарядки первоначально нейтральной частицы с удельной объемной проводимостью γ₁ < 0,25×10^-9Ом^-1×м^-1, находящейся на некоронирующем электроде определяется по формуле (1).

Допустим, что в момент t₁ напряжение мгновенно понижается до U₂, причем U₁>U₂>U_hk. С момента t₁ в зависимости от значения накопленного заряда q₁, и значения U₂ может происходить дальнейшая зарядка частиц или разрядка на осадительный электрод. Если до момента t₁ частица зарядилась недостаточно и при U₁ нормальная слагающая поля в воздушной среде на поверхности эллипсоидальной частицы Е_2n не изменит направления, то частица продолжает заряжаться от объемного заряда. Постоянная времени зарядки остается прежней. Режим насыщения процесса зарядки в каждой точке поверхности полуэллипсоидальной частицы наступит при выполнении равенства

γ₁ Е_1n = γ₂ Е_2n

Разрядка частицы на осадительный электрод возможна, если при U₂ нормальная слагающая поля в воздухе Е_2n изменит направление, т.е. Е_2n < 0.

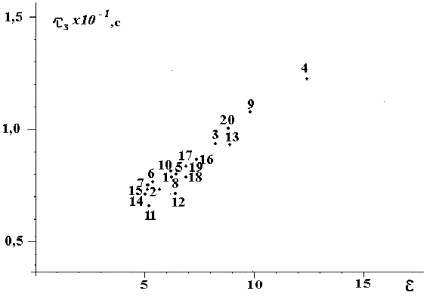
Рисунок

В этом случае постоянная времени разрядки частицы на осадительный электрод из-за наличия объемной проводимости среды, определяется выражением (1). Другими словами, если за время t₁ при U₁ частица успела зарядиться до близкого к предельному значению, то при понижении напряжения до U₂ вследствие изменения направления Е_2n зарядка частицы ионизацией прекратится. Вблизи поверхности частицы образуется зона, свободная от носителей зарядов. Разрядка частицы будет продолжаться до тех пор, пока направление нормальной слагающей поля не станет положительным. В случае U_2n < U_нк или U₂ =0 объемная проводимость среды практически равна нулю.

Расчеты производились по усредненным параметрам γ₁ и γ₂, . Усреднение значений удельной объемной проводимости некоторых минералов производилось с учетом результатов электрической сепарации коллективных концентратов в промышленных условиях.

Зависимость τ_з(ε) для некоторых минералов приводится на рисунке.

На основании расчетных параметров, полученных на примере реально существующих минералов, можно сделать следующие выводы:

– преобладающее влияние на величину постоянной времени зарядки плохо проводящих частиц оказывает их диэлектрическая проницаемость;

– с увеличением диэлектрической проницаемости постоянная времени зарядки возрастает.

Литература

1. Osborn J.A. Demagnetizing factors of the general ellipsoid. Phys. Rev., 1945, vol. 67, N 11 - 12

2. Джуварлы Ч.М., Вечхайэер Г.В., Штейншрайбер, В.Я. Трехосный диэлектрический элипсоид в электрическом поле при учете проводимости. - Изв. АН СССР, Энергетика и транспорт, 1969, №- I, с. 158-162.

3. И.П. Верещагин, В.И. Левитов, Г.З. Мирзабекян, М.М. Пашин. Основы электрогазодинамики дисперсных систем. М., Энергия, 1974,с. 480.