Федорченко С.Г., Федорченко Г.С.

Приднестровский государственный Университет, г. Тирасполь

АЛГОРИТМ ФОРМИРОВАНИЯ ИНТЕГРАЛЬНОГО ПОКАЗАТЕЛЯ СОСТОЯНИЯ ЭНЕРГЕТИЧЕСКОЙ БЕЗОПАСНОСТИ

При решении задачи управления реальным объектом, необходимо, в качестве первого шага описать состояние объекта. Как правило, это описание содержит некий набор характеристик объектов, которые или оцениваются экспертом. Для управления объектом крайне желательно свести весь этот массив данных к одному числу – некоторому интегральному показателю, который бы в полной мере (в соответствии с поставленной задачей управления) описывал состояние объекта.

В литературе [1] предложен алгоритм формирования интегрального показателя энергобезопасности, основанный на использовании индикативного анализа. В основе индикативного анализа является формирование системы индикаторов, отражающих основные процессы в объекте исследования.

Система индикаторов может иметь подсистемы (блоки) которые в свою очередь также могут содержать некие подблоки и т.п., т.е система индикаторов может иметь иерархическую структуру.

Классификация состояний осуществляется по шкале кризисности, сформированной для каждого индикатора отдельно. В [1, с. 21] предлагается следующее построение шкалы кризисности:

- нормальная ситуация – 1 балл;

- предкризисное начальное -2 балла;

- предкризисное развивающееся- 3 балла;

- предкризисное критическое – 4 балла;

- кризисное нестабильное – 5 баллов;

- кризисное угрожающее – 6 баллов;

- кризисное критическое – 7 баллов;

- кризисное чрезвычайное – 8 баллов.

После того, как для всех индикаторов построены шкалы кризисности, получены значения индикаторов, и найдены соответствующие значения баллов, рекомендуется найти среднее значение баллов для каждого блока (если все индикаторы одинаково важны) или средневзвешенное значение баллов (если важность индикаторов различна).

Выполнив эти действия для каждого блока индикаторов, мы можем найти среднее (или средневзвешенное) значение блочных индикаторов, в результате чего мы получим интегральный показатель, характеризующий состояние объекта управления, например, энергетического комплекса.

Однако такой подход обладает рядом недостатков, главный из которых, по нашему мнению - его не универсальность. Рассмотрим два случая.

1. Негативное значение одного индикатора может быть скомпенсировано положительным значением другого, например неравномерность поставок топлива компенсируется имеющимися запасами топлива.

2. Негативное значение одного индикатора сводит на нет все сколь угодно благополучные значения других индикаторов, например, острая нехватка генерирующих мощностей сводит на нет наличие современной системы электроснабжения.

В первом случае мы можем абсолютно обоснованно строить привычный аддитивный интегральный показатель – например среднее арифметическое используемых индикаторов. Во втором случае нам необходимо использовать мультипликативный интегральный показатель, в процессе формирования которого мы используем произведение индикаторов.

Предлагается для построения мультипликативного интегрального показателя использовать обобщенную функцию полезности Харрингтона-Мечера [3, 4]. Здесь значение частного отклика, переведённое в безразмерную шкалу желательности, обозначается через d_i (i=1, 2, …, n) и называется частной желательностью (от desirable фр. - желательный). Шкала желательности имеет интервал от нуля до единицы. Значение d_i=0 соответствует абсолютно неприемлемому уровню данного свойства, а значение d_i=1 – самому лучшему значению свойства [3, 4] (см. табл. 1).

Таблица 1 – Связь между количественными значениями безразмерной шкалы и психологическим восприятием человека

Желательность	di
Очень хорошо	1,00 – 0,80
Хорошо	0,80 – 0,63
Удовлетворительно	0,63 – 0,37
Плохо	0,37 – 0,20
Очень плохо	0,20 – 0,00

Обобщённая функция желательности может быть найдена по формуле

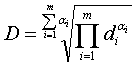, (1)

где m – число частных оценок качества (число сравниваемых откликов); d_i – частный критерий отклика; α_i –вес – i-го частного критерия.

При использовании обобщенной функции полезности необходимо удовлетворить требованию - среди частных откликов не должно быть коррелированных между собой (в крайнем случае, допускается с оговорками пренебрежимо слабая корреляция). Для решения этой задачи рекомендуется использовать метод корреляционных плеяд [3, 4].

Используем уровни энергетической безопасности, описанные выше, и попытаемся состыковать их со значениями функции полезности. Результат представлен в табл. 2.

Прокомментируем это разбиение области существования d- функции:

1) нормальное состояние, совершенно очевидно соответствует значениям d- функции 1-0,63 («очень хорошо» и «хорошо»);

2) разобьем половину интервала 0,63-0,37 («удовлетворительно») на две равные части, первую из которых (0,63-0,5) отнесем к состоянию «предкризисное начальное»;

3) вторую половину интервала 0,63-0,37 (0,5-0,37) разделим еще на две равные части 0,5-0,44 и 0,44-0,37 которые отнесем к состояниям «Предкризисное развивающееся» и «Предкризисное критическое», соответственно;

4) область значений d-функции 0,37-0,2 («плохо») разделим на три равные области 0,37-0,31; 0,31-0,26; 0,26-0,2, которые отнесем к состояниям «Кризисное нестабильное», «Кризисное угрожающее» и «Кризисное критическое», соответственно;

5) область значений d-функции 0,2-0 («очень плохо») отнесем к состоянию «Кризисное чрезвычайное».

Таблица 2. – Состояния (уровни) энергетической безопасности, состыкованные со значениями функции полезности

№ п/п	Название состояния	Кол-во баллов	Ситуация	Значения d-функции
1	Нормальное	1	Нормальная	1-0,63
2	Предкризисное начальное	2	Предкризисная	0,63-0,5
3	Предкризисное развивающееся	3		0,5-0,44
4	Предкризисное критическое	4		0,44-0,37
5	Кризисное нестабильное	5	Кризисная	0,37-0,31
6	Кризисное угрожающее	6		0,31-0,26
7	Кризисное критическое	7		0,26-0,2
8	Кризисное чрезвычайное	8		0,2-0

Таким образом, алгоритм формирования интегрального показателя уровня энергетической безопасности выглядит следующим образом:

1. Формируется список показателей, характеризующих энергетическую безопасность.

2. Полученный список разбивается на группы, в каждой группе присутствуют показатели, значения которых взаимно компенсируют друг с друга (как со знаком плюс, так и со знаком минус) – для каждой группы формируется свой аддитивный интегральный показатель (среднее или средневзвешенное значение); ряд групп состоит из одного показателя, для них интегральный показатель не формируется.

3. С учетом п. 2 формируется новый список показателей, куда вместо ряда групп показателей включается их интегральный аддитивный показатель.

4. Для показателей из нового списка необходимо сформировать интегральный мультипликативный показатель, с этой целью:

- с помощью метода корреляционных плеяд, формируют список независимых показателей;

- по всему перечню независимых показателей формируют весовые коэффициенты;

- определяют по каждому независимому показателю границы уровней энергетической безопасности;

- вычисляют значения частных функций полезности;

- вычисляют значение обобщенной функции полезности.

Авторами, используя вышеописанный подход, был произведено вычисление интегрального показателя энергетической безопасности на примере Республики Молдова.

Литература

[1] Методические подходы к решению проблемы энергетической безопасности Молдовы и Белоруси / Быкова Е.В., Михайлевич А.А., Постолатий В.М. и др.; Акад наук Молдовы, Ин-т энергетики, Нац. Акад. Наук Белоруси и др. – К.:Б. и., 2010 (Tipogr. ASM). – 100 p.

[2] В. В. Бушуев, Н. И. Воропай, А.М. Мастепанов, Ю. К. Шафраник и др. Энергетическая безопасность России. Новосибирск: Наука. Сибирская издательская фирма РАН, 1998, 302 с.

[3] Обобщенная функция полезности и ее приложения. /Авт.: С.Г. Федорченко, Ю.А. Долгов, А.В. Кирсанова, Э.М. Менчер, С.В. Помян, М.В. Нижегородова, Е.И. Андрианова, Н.В. Колоскова, А.В. Колегов, А.М. Башкатов. /Под ред. С.Г. Федорченко. – Тирасполь: Изд-во Приднестр. университета, 2011. – 196с. – (в обл.) ISBN 978-9975-4062-3-9/

[4] Долгов Ю.А. Статистическое моделирование. – Тирасполь: РИО ПГУ, 2002. – 280 с.