ВЫБОР ФОРМЫ ШИН ДЛЯ ПИТАНИЯ ПОТРЕБИТЕЛЕЙ БОЛЬШОЙ МОЩНОСТИ

Соборницкий В.И., Павлюс С.Г., Замурников В.М.,

Папанова И.И..

ГВУЗ «Украинский государственный химико-технологический университет»

Электроснабжение потребителей большой мощности, в частности, ферросплавных печей мощностью до 100 МВА током промышленной частоты приводит к снижению коэффициента мощности (cosφ) до 0,8 – 0,85 за счет большого индуктивного сопротивления короткой сети.

Применение токов пониженной частоты (10 – 30 ГЦ) для снижения индуктивного сопротивления короткой сети и повышения коэффициента мощности должно решать данную проблему. Однако, наличие преобразователя частоты между печным трансформатором и печью увеличивает длину короткой сети и, следовательно, ее индуктивность.

В общем виде собственная индуктивность линейного провода может быть представлена в виде

L = N – G + A – Q, где [1]

N – величина, зависящая только от формы и размеров оси провода и не зависящая от формы и размеров поперечного сечения провода и от характера распределения тока по сечению. N находят методом численного интегрирования; G, A, Q – величины, зависящие от формы и размеров поперечного сечения и от характера распределения тока по сечению. G, A и Q приближено находятся из формул:

, где [2]

g, a, q – соответственно среднее геометрическое, среднее арифметическое и среднее квадратичное расстояние площади поперечного сечения провода от самой себя; l – длина оси провода; D – расстояние между крайними точками оси провода.

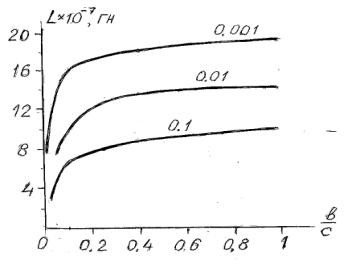
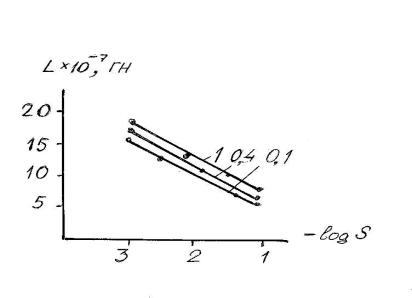
Таким образом, индуктивность можно изменить, изменяя геометрические параметры короткой сети. Шины короткой сети обычно имеют прямоугольную форму. При низкой частоте для расчета индуктивности была использована формула

, где [3]

и c - стороны прямоугольника, являющегося его поперечным сечением. Результаты расчета индуктивностей при S= b·c = const и l = const приведены на рисунке 1.

Рис.1. Зависимость L от b/c. Цифрами на кривих показано сечение шины.

На величину индуктивности существенное влияние оказывает сечение шины. На рисунке 2 показана зависимость индуктивности шин от их поперечного сечении. При этом плотность тока должна оставаться неизменной, как и сила тока, протекающего по шине.

Рис.2. Зависимость индуктивности шин от их поперечного сечения. Цифрами на кривых показано соотношение b/c.

Поскольку, с увеличением поперечного сечения индуктивность уменьшается, то в данном случае возможно использование полых шин. С некоторым допущением было принято, что сечение такой шины равно индуктивности наружного, т.е. большего прямоугольника S_н. При этом разность между сечениями наружного S_н и внутреннего (полого) прямоугольника должна оставаться постоянной и равной активному сечению S, по которому протекает ток.

В таблице приведены значения индуктивности, толщины стенки полой шины и наружного поперечного сечения S_н для S = 0,01 и b/c = 0,1.

L x 10^-7, гн	11,6	9,8	9,16	8,4
t, м	-	0,113	0,09	00,85
Sн, м^2	0,01	0,025	0,036	0,049

В первом столбце указаны параметры сплошной шины. Как видно из таблицы, при переходе от сплошной шины к полой с увеличением S_н в 4 раза, индуктивность снижается на 28%.