Технические науки/6. Электротехника и радиоэлектроника

Нивин А.Е., к.т.н. Саушев А.В., Троян Д.И., д.т.н. Шошмин В.А.

Государственный университет морского и речного флота

имени адмирала С.О. Макарова, Россия

Метод идентификации систем управления

автоматизированных электроприводов

В настоящее время самое широкое применение на практике находят автоматизированные электроприводы с частотным регулированием скорости, построенные по принципу подчиненного регулирования координат. Необходимым условием успешной работы электроприводов является идентификация их систем управления в реальном масштабе времени. В докладе рассматривается один из возможных подходов к решению задачи идентификации системы управления на примере регулятора скорости.

Под идентификацией обычно понимают определение структуры и параметров математической модели, которые обеспечивают наилучшую близость выходных величин модели и объекта при одинаковых входных воздействиях [1].

Комплекс задач идентификации модели системы управления (СУ) электропривода обычно включает три этапа. На первом этапе выбирают структуру модели по результатам изучения СУ или имеющимся априорным сведениям (структурная идентификация), на втором – критерий подобия (близости) модели и СУ, на третьем – по экспериментальным данным определяют параметры модели, исходя из выбранного критерия (параметрическая идентификация).

Одним из перспективных методов оценки технического состояния сложных систем управления является идентификация по динамическим характеристикам, которая отличается широкими возможностями фильтрации помех и возмущений. При этом актуальным является метод идентификации линейных динамических систем на основе ортогональных фильтров Лаггера [2]. Вместе с тем, с целью идентификации СУ в реальном масштабе времени, востребованными являются методы, непосредственно основанные на построенных частотных характеристик СУ электроприводами.

С точки зрения теории автоматического регулирования [3] СУ электропривода обычно включают в себя динамические звенья первого порядка. В качестве примера рассмотрим ПИ-регулятор, который имеет частотную характеристику вида

.

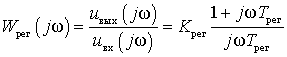Целью идентификации подобного звена является определение статического коэффициента преобразования и постоянной времени . Эта операция может быть выполнена несколькими способами, например, по амплитудно-фазовой характеристике или логарифмической частотной характеристике звена. Однако наибольшая точность идентификации достигается при использовании квадрата модуля частотной характеристики

.

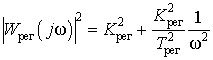Эта функция линеаризуется в координатах и следующим образом:

,

где коэффициенты ; .

Таким образом, можно рекомендовать следующий порядок идентификации ПИ–регуляторов электропривода:

– при помощи экспериментальных данных измерения амплитудных значений входного и выходного сигналов, строится амплитудно-частотная характеристика динамического звена;

– в координатах (–) наносятся экспериментальные точки квадрата модуля этой характеристики на график;

– проводится прямая линия, аппроксимирующая семейство экспериментальных точек и по графику или аналитически определяются параметры a и b аппроксимирующей прямой.

Параметр a равен отрезку, отсекаемому прямой на оси ординат. Параметр b является угловым коэффициентом прямой:

;

, – масштабы по осям.

В заключение определяются параметры исследуемого звена:

; .

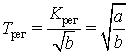Анализ, разработка и применение методов идентификации СУ и способов оценки их текущего состояния позволяют повысить эффективность эксплуатации электроприводов, а также обеспечить автоматическую настройку их параметров в процессе работы.

Литература

1. Алексеев А. А., Кораблев Ю. А., Шестопалов М. Ю. Идентификация и диагностика систем. – М.: Академия, 2009. – 352 с.

2. Нивин А.Е., Саушев А.В., Шошмин В.А. Синтез ортогональных фильтров при статистической идентификации динамических систем. Известия ВУЗов. Приборостроение, № 10 – 2013. С. 5–11.

3. Егупов Н.Д., Пупков К.А. Методы классической и современной теории автоматического управления. Том. 2. Статистическая динамика и идентификация систем автоматического управления. – М.: МГТУ им. Н.Э Баумана, 2004. – 640 с.