Технические науки/8. Обработка материалов в машиностроении

к.т.н. Ракунов Ю.П., д.т.н. Абрамов В.В.

Московский государственный строительный университет, Россия

Аналитический метод определения сил резания
при тонкой механической обработке

Развитие метода точного аналитического определения сил резания встречает ряд противоречий и затруднений, вызванных сложностью процесса резания, и различием условий процесса тонкой механической обработки. Многообразная геометрия режущих инструментов, широкие диапазоны подачи и глубины резания и особенно большие пределы скорости резания при обработке металлов затрудняют решение поставленной задачи.

Целью настоящей работы является теоретическое определение действующих сил, напряжений и деформаций в тонком срезаемом слое, используя закономерности физики твёрдого тела и теории пластичности.

Устанавливая механическое равновесие внешних и внутренних усилий, исследователи обычно относят силу резания P_z только к площади снимаемого слоя a∙b или только к площади сечения стружки a₁∙b, считая силу равномерно распределённой по контактной площадке. Этим приёмом устраняются затруднения, связанные с закономерностями распределения напряжений, а область, лежащая под линией среза, не рассматривается, хотя на её отдельных участках значения напряжений не меньше, чем в стружке.

Такое применение принципа механического равновесия происходит чисто формально и приводит к большим ошибкам, т.к. сила P_z приравнивается не к сумме напряжений, действующих во всей деформируемой области, а только к части напряжений, действующих в отделяемом слое. При вычислении подобным образом величина напряжений получается во много раз превышающей предел текучести обрабатываемого материала и применение условия пластичности для определения величины силы резания становится совершенно невозможным.

Нарушение принципа механического равновесия приводит во всех случаях к неправильным результатам. Очевидно, что силу, вызывающую напряжённое состояние в целой области, нельзя приравнивать напряжениям, суммированным в произвольно выбранной зоне, как нельзя целое приравнивать его части. Поэтому вопрос о распределении напряжений в деформируемой области становится очень важным для точного определения деформирующей силы.

Решение поставленной задачи, поэтому, представляет как теоретический, так и практический интерес, охватывая область тонкой финишной обработке при толщине срезаемого слоя a= 0,01…0,07 мм.

Анализ действующих сил и распределения напряжений при малой толщине среза облегчается условиями, учитывая которые условия, можно рассматривать следующую систему действующих сил при срезании тонких слоёв металла (рис. 1).

Наличие этих сил в процессе резания может быть легко установлено непосредственным измерением их с помощью двухкомпонентного динамометра, что очень важно для проверки следующих далее выводов.

Напряжённое состояние, вызываемое силами P_z и P_у или их равнодействующей R – это радиальное распределение напряжений [1].

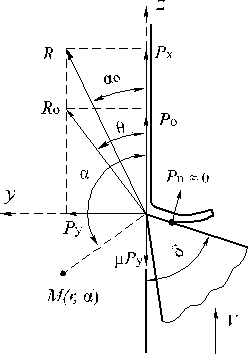
Рис. 1. Силы резания при отделении тонких стружек

σr = –

2R πr

(cosα ∙ cosαo + sinα ∙ sinαo) = –

2R πr

cos (α – αo), (1)

где: σ_r – радиальное напряжение в (∙)М, действующее по направлению к режущему лезвию, т.е. к точке приложения силы R;

r, α – полярные координаты (∙)М, причём угол α отсчитывается от оси OZ против часовой стрелки. Сравнение формулы (1) с формулой радиальных напряжений при неограниченной а [2], показывает, что она отличается только значениями коэффициентов k₁ и k₂, учитывающими влияние толщины среза a и угла резания δ.

Приравнивая равные части этих двух формул:

σr = –

2R πr

(cosα ∙ cosαo + sinα ∙ sinαo) = –

2R r

(

сosα k1

+

sinα k2

),

откуда следует, что значения коэффициентов k₁ и k₂ для формулы (1):

k1 =

π__ cosαo

; k2 =

π__ sinαo

.

(2)

Отношение этих коэффициентов имеет большое значение при анализе напряжённого состояния в зоне резания, т.к. представляет собой отношение между двумя полями напряжений в деформируемой области и является характеристикой асимметрии распределение напряжений. Величина
k_о = k₁/ k₂, названная коэффициентом асимметрии напряжённого состояния, для случая, описываемого формулой (1),

kо =

k1 k2

=

π ∙ sinαo π ∙ соsαo

= tg αo.

(3)

Из схемы сил, рис.2, видно, что

kо = tgαo =

Py Pz

(4)

Однако при движении резца сила P_y вызывает появление новой, также реактивной, силы трения, величина которой

P_y ∙ tgφ = P_z μ

где: φ – угол трения, а μ – коэффициент трения. Сила трения на задней грани оказывает сопротивление движению резца и имеет направление, противоположенное силе P_z; поэтому часть силы P_z будет затрачена на преодоление силы трения и действительными деформирующими силами будут силы P_о и P_у или их равнодействующая R_o. (см. рис.2). Величина силы Р_о определяется

Po = Pz –Pу tgφ = Pz (1 – tgαo tgφ) = Pz (1 – ko μ) =Py (

1 – μ ∙ ko ko

).

(5)

Сила R_o является равнодействующей новой системы сил, в которую включена сила трения на задней грани. Величина силы R_o легко вычисляется из соотношения

Rо =

Po_ cosθ

=

Py_ sinθ

,

(6)

где: θ – угол наклона равнодействующей R_o к оси OZ.

Значения угла θ можно определить из соотношения (5):

tgθ = Py / Pо = tgαo / (1 – tgαo tgφ) = ko / (1 – μ ∙ ko).

(7)

Величина tgθ является новым коэффициентом асимметрии, изменившимся вследствие влияния силы трения на задней грани. В общем случае tgθ зависит также от других факторов, особенно от толщины среза а, угла резания δ (переднего угла γ) и скорости резания V; в нашей задаче влияние этих факторов пока не учитывается и, так как коэффициент трения μ в выражении (7) очень трудно определить экспериментальным путём, мы сохраним в последующих выводах значение К_о из выражения (3) и (4).

Новая система сил с равнодействующей R_o аналогична предыдущей, поэтому решение задачи по распределению напряжений в деформируемой зоне при использовании формулы (1) можно получить, подставив в неё вместо силы R – силу R_o, а вместо угла α₀ – угол θ. Тогда радиальные напряжения

σr = –

2Ro πr

(cosα ∙ cosθ + sinα ∙ sinθ)

(8)

Если вынести за скобки cosθ и использовать формулу (6), получим:

σr = –

2Po πr

(cosα + sinα ∙ tgθ)

Далее, внося значение силы Р_z из выражения (5) и величину tgθ из (7), получим формулу радиальных напряжений в виде

σr = –

2Pz πr

[(cosα (1 – tgαo + tgφ) + sinα ∙ tgαo]

(9)

По этой формуле можно при любой заданной силе Р_z рассчитывать σ_r в любой точке и построить линии равных радиальных напряжений или же, используя формулы для преобразования координат, вычислить и построить эпюры нормальных и касательных напряжений в любом сечении деформируемой зоны.

Для выяснения условий начала скольжения элементарных слоёв в отделяемой тонкой части среза можно, не определяя компонент напряжений в декартовых координатах, применить условие пластичности в полярных координатах, которое для плоского деформированного состояния записывается [1]

(σ_r – σ_α)² + 4τ_rα² = 4K_s² (10)

При радиальном распределении напряжений σ_α и τ_rα равны нулю; поэтому условие пластичности (10) принимает следующий вид:

σ_r = 2K_s = 2 ∙ 0,577σ_т = 1,154σ_т (11)

где: К_s – константа пластичности без учёта упрочнения материала;

σ_т – предел текучести материала.

Возможность применения условия пластичности без учёта упрочнения срезаемого слоя можно обосновать следующими данными. Известно, что зона массового сдвига зёрен проходит от режущей кромки резца к внешней поверхности среза под углом β (рис. 3). Угол β, соответствующий наибольшим касательным напряжениям, можно определить по известной формуле, устанавливающей связь угла β с углом асимметрии α_о [2]:

β + α_о = π/4; β = 45^о – α_о (12)

Впереди зоны максимума, т.е. до линии ОА, происходят только малые пластические деформации в отдельных наиболее мягких и удачно ориентированных зёрнах металла, что подтверждается анализом микротвёрдости [3] в различных точках зоны резания. В зоне максимума, начиная с линии ОА, происходит основная деформация, вызывающая большое упрочнение. Вследствие быстрого движения зоны сдвига и большой степени упрочнения, ширина зоны сдвига остаётся очень малой. Так, в работе [4] установлено, что ширина зоны сдвига зависит от толщины среза а и составляет примерно 0,05а, Несмотря на узость зоны сдвига, линия ОА является границей и началом основной деформации сдвига (рис. 2).

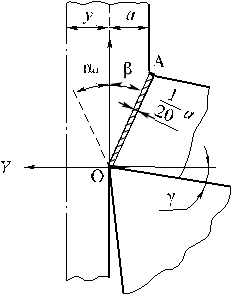
Рис. 2. Величина и положение зон сдвига и упрочнения

Радиальные и касательные напряжения неравномерны по линии ОА: около (∙) О (вершины режущего клина) напряжения очень велики, и материал деформируется по многим направлениям; далее к (∙) А напряжения убывают, и около свободной поверхности среза они имеют меньшее значение. Пластическая деформация по всей плоскости сдвига будет возможна лишь в том случае, если в (∙) А касательные напряжения достигнут значения константы пластичности К_s, поэтому именно в (∙) А, как граничной точке между неупрочнённым и упрочняющимся металлом, может быть применено условие пластичности без упрочнения [5].

Перейдём к выводу формулы для определения силы Р_z, установив возможность применения условия пластичности (11). Подставляя в уравнение (11) значение σ_r из (9), а вместо радиуса r = ОА, его значение, выраженное через толщину среза α, и переменный угол α из отношения r∙sinα=а, получим выражение для наибольшего касательного напряжения, действующего в плоскости ОА около (∙)А. Подставляя далее вместо переменного угла α его значение, соответствующее наклону плоскости ОА, т.е. угол β из формулы (12), и, внося значение ширины среза b (т.к. сила отнесена к единице ширины среза), получим:

Ks = 0,577σт = –

Pz_ πab

[1 – tgαo ∙ tgφ)+ tgαo ∙ sin^2β)]

(13)

Величина π в этом выражении представляет собой частное значение коэффициента К₁ = π при толщине среза а = 0 (экстраполяция на нулевую толщину среза), поэтому целесообразно внести в формулу коэффициент К₁, имеющий более широкое значение и учитывающий влияние других факторов. Внося принятые обозначения К_о и μ, а также опуская знак (–) в правой части, будем иметь:

Ks = 0,577σт =

Pzsin2β 2ab k1

[1 – ko (μ + tgβ)] (

( (14)

Решив это уравнение относительно Р_z, получим формулу активной силы резания Р_z при малой толщине среза с учётом влияния силы трения на задней грани резца:

Pz = =

1,154σт a∙b∙k1____ sin2β [1 – ko (μ+tgβ)]

(15)

Формула (15) получена аналитическим путём на основе решения задачи о распределении напряжений во всей деформируемой области, причём, в выводах нет никаких допущений, искажающих физический смысл явлений, имеющих место в процессе резания. Формула выведена для малой толщины среза и поэтому не является универсальной, применимой для всех многообразных случаев резания [6]. Решение задачи для большой толщины среза а с учётом влияния угла резания δ показывает, что тип формулы (15) может применяться, а влияние α и δ изменяет лишь значения коэффициентов k₁ и k_о.

С увеличением толщины среза а жёсткость стружки возрастает, оказывая воздействие на переднюю грань резца, вызывая изгиб стружки и создавая момент вокруг (∙)О. В условиях пластической деформации этот момент не может быть сложен с силой Р_z. Тенденция изменения k₁ и k_о при увеличении а и изменении δ (или переднего угла γ) очень видна при проверке формулы (15) по опытным данным. Коэффициент k₁ характеризует полный угол деформируемой области в полярных координатах, а коэффициент асимметрии k_о – отношение между двумя полями напряжений в этой области. Когда деформируемая область возрастает (с увеличением а и γ), значения k₁ увеличивается, а k_о – уменьшается, причём, k_о более чувствителен к изменениям а и γ, чем k₁.

Для проверки формулы (15) было проведено сравнение сил Р₂ и Р_у (см. рис.4), вычисленных по формулам (13) и (15) с экспериментальными данными, полученными при сводном резании стали 20Х с толщинами среза а = 0,01; 0,02; 0,04 и 0,07 мм при ширине среза b = 5 мм и γ = 20^о. Средние значения k₁ и k_о для всех величин а и γ = 20^о; k₁ =3,54, k_о =0,457; т.е. угол скольжения β = 20^о20΄. Значения коэффициентов трения μ были рассчитаны по формуле:

μ = =

1 Ру

[(Pz – Py ∙ tgβ) ---

1,154σт ∙а∙b∙k1 sin2β

],

(16)

полученной из формулы (15), подстановкой значения k_о из отношения (4).

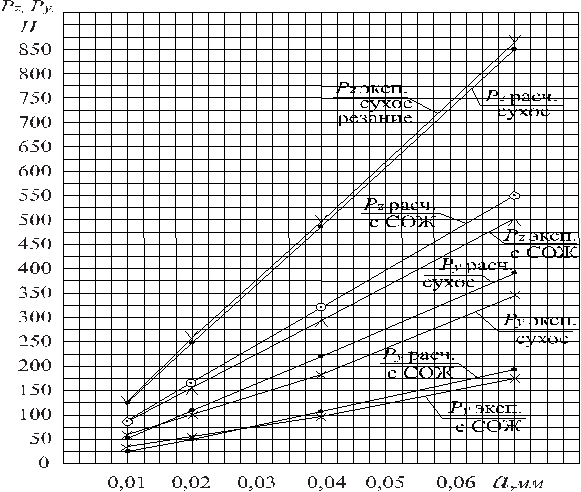
Рис. 4. Сравнение сил P_z и Р_у, полученных расчётным и экспериментальным путём

Значения μ были установлены: для сухого резания μ_с = 0,36; а для резания в среде четырёххлористого углерода (ССl₄) μ = 0,21.

Сравнение расчётных и опытных значений сил P_z и Р_у показывает хорошее совпадение результатов, если учесть, что значения k₁ и k_о должны быть переменными даже в указанном диапазоне изменения а. Кроме того, не все опытные данные достаточно точны, т.к. точное измерение малых значений сил резания (особенно Р_у) индикаторным динамометром затруднительно. Более точные и надёжные результаты можно получить при использовании цифрового динамометра Dyna-Z с диапазоном измерения от 10 до 3000 Н, разработанном ООО «Технолог» (г. Рыбинск) [7].

ВЫВОДЫ

Решение поставленной задач позволяет сделать следующие выводы.

1. Действие системы сил, приложенных к режущему клину в процессе резания, приводит к радиальному распределению напряжений в деформируемой зоне, что подтверждается расчётно-аналитическим методом исследования.

2. Радиальные и касательные напряжения распределены неравномерно: в пределах радиуса округления режущего клина напряжения настолько велики, что материал пластически деформируется по всем направлениям, вызывая упрочнение металла. Во всех других точках напряжения σ_r обратно пропорциональны радиусу r и убывают по мере удаления от зоны приложения силы.

3. Максимум касательных напряжений определяет угол скольжения β и ширину зоны массового сдвига зёрен при эстафетной передаче деформации.

4. Реактивная сила Р_у вызвана и обусловлена асимметрией напряжённого состояния в деформируемой области и характеризуется коэффициентом асимметрии, от величины и знака которого зависит глубина проникновения деформации в поверхностном слое обрабатываемой заготовки.

5. Напряжения в области, ниже линии среза, у вершины резца выше, чем в зоне среза, что вызывает деформацию и упрочнение верхнего слоя металла на обрабатываемой поверхности.

6. Значения сил Р_z и Р_у, а также силы трения μ∙Р_у с достаточной степенью точности рассчитываются по аналитическим формулам, а при наличии точных динамометрических значений Р_z и Р_у может быть определена величина коэффициента трения μ для заданных условий резания.

7. Экспериментальные исследования показывают, что коэффициент трения μ зависит от переднего угла γ, от шероховатости передней поверхности режущего клина и от степени его износа по задней поверхности.

ЛИТЕРАТУРА

1. Соколовский В.В. Теория пластичности. ГИТТЛ, 1950.

2. Апраксин В.И. Некоторые вопросы теории скоростного резания. Сборник. «Прогрессивная технология машиностроения», Ч. III, ЛОНИТОМАШ, 1962.

3. Drucker D.C. An Analysis of the Mechanics of Metal Cutting. Journal of Applied Physics, № 11, 1949.

4. Зорев Н.Н. Расчёт проекций сил резания.– М.: Машиностроение, 1958.– 54 с.

5. Розенберг Ю.А. Методы аналитического определения степени деформации металла стружки при резании // Вестник машиностроения, 2001. – № 3. – С. 34-38.

6. Рыкунов Н.М. Повышение эффективности тонкого точения, исходя из достижимых показателей качества деталей и технологических возможностей процесса: Автореф. дис. д-ра техн. наук, М., 1999. – 30 с.

7. Электронный ресурс www.ooo-technolog.ru.