О.Л. Бозиев

Кабардино-Балкарский государственный университет (г.Нальчик, Россия)

Решение нагруженного гиперболического уравнения

приближенно-аналитическим методом

Решение u = u(x,t) нагруженного уравнения вида

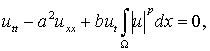(1)

при p ≥ 3, a, b > 0, будем искать в области Q = Ω×(0,T), Ω = (0,l), при условиях

u(x,0) = 0, u_t(x,0) = 0, 0 ≤ x ≤ l, (2)

u(0,t) = ψ₁(t), u(l,t) = ψ₂(t), 0 ≤ t ≤ T. (3)

За счет интегрирования степенного сомножителя по пространственной переменной уравнение (1) представляет собой модификацию нелинейного гиперболического уравнения, описывающего ряд сложных физических процессов.

В настоящей работе приведен способ нахождения приближенного решения задачи (1) – (3), использующий априорные оценки решений поставленной задачи. Этот способ был применен в [1] для решения уравнения (1) при неоднородных начальных и однородных граничных условиях.

Потребуем, чтобы ψ₁(t), ψ₂(t) Î C¹[0,T].

Установим некоторые априорные оценки решения задачи, необходимые для нахождения ее приближенного решения. Для этого (1) сначала умножим скалярно на функцию u_t , и заметив что

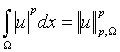(4)

выражает норму функции u в пространстве L_p(Ω), после несложных преобразований приходим к неравенствам

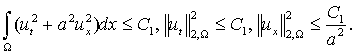(5)

Затем умножим (1) скалярно на u^p-1 и преобразуем произведение к виду

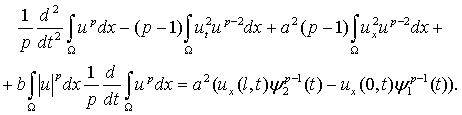
Последнее уравнение умножим на sgn^pu и после интегрирования по t в границах от 0 до t будем иметь

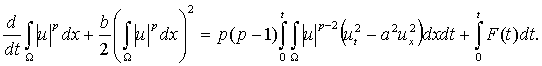
Применяя к слагаемым известные неравенства Гёльдера и Фридрихса, а также (5) и свойства функций u_x(0,t) и u_x(l,t), перейдем к соотношению

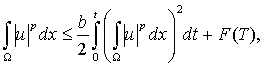
Далее воспользуемся нелинейным интегральным неравенством [2, с.22], которое

приводит к выполняющейся для всех t Î [0, T] оценке

(6)

с функцией

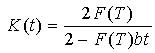
Перейдем к нахождению приближенного решения задачи (1) – (3). Для этого дважды проинтегрируем (1) по x в границах от 0 до x, устремляя при первом интегрировании x к l в верхней границе интеграла [1], что приводит к выражению

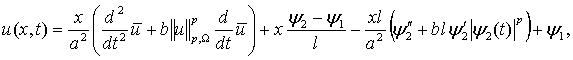(7)

в котором От (7) интегрированием по x в границах [0, l] приходим к обыкновенному дифференциальному уравнению

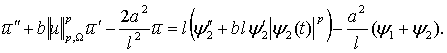(8)

Необходимые для его интегрирования начальные условия получим из условий (2):

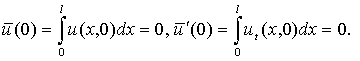(9)

Линеаризуем (8) выбором правой части (6) таким образом, чтобы оно выполнялось как равенство, и аппроксимируем (8) линейным уравнением

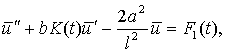(10)

где

Найденную путем решения задачи (10), (9) функцию необходимо подставить в (7) вместе с соответствующей функцией , чтобы получить формулу для нахождения приближенного решения задачи (1) – (3).

Предлагаемый способ использования априорной оценки решения поставленной задачи может быть полезным для нахождения решений дифференциальных уравнений в частных производных со степенной нелинейностью. При этом за искомое приближенное решение следует принять решение исходной задачи для ассоциированного нагруженного уравнения.

Литература

1. Бозиев О.Л. Приближенное решение смешанной задачи с однородными граничными условиями для нагруженного гиперболического уравнения// Материалы международной научно-практической конференции «Глобальные вызовы современности и проблемы устойчивого развития юга России». Россия, Кабардино-Балкарская Республика, г. Нальчик, 14 – 16 октября 2015 г. С. 288 – 291.

2. Филатов А. Н., Шарова Л. В. Интегральные неравенства и теория нелинейных колебаний. – М.: Наука, 1976. – 151 с.