УДК 62-50:663

ТЕХНОЛОГИЯЛЫҚ ПРОЦЕСТЕРДІ ҮЙРЕНУДЕ МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУДІҢ ОРНЫ

Исмайылов Аманкелди Есиркегенович,к.т.н., старший.преподаватель, Алматинский технологический университет,

Айтбаева Рахатай Бекбергеновна, старший.преподаватель,

Жумагельдиев Амангелді студентка 4-курса

Технологиялық процестерді қалай үйренуге болады? Бұл мәселені шешу кілтін математикалық модельдеу береді. Бұл тәсіл жүйелік талдау стратегиясына негізделелді. Бұл жобаның маңызы-процесті күрделі өзара әсерлесуші иеарархиялық жүйе деп, оның құрылымын сапалы бақылап, математикалық өрнегін жасап шығу және белгісіз параметрлерін бағалау болып табылады [1].

Мысалы, сұйық ортада бөлшектер тамшылар немесе газ көпіршіктерінің қосылу немесе өзара әрекеттесу процесінде пайда болған оқиғалар қарастырылғанда, сапалық иеарархиясының бес деңгейі ажыратылады:

1.Атомдық-молекуляр деңгейдегі жағдайлар жиыны

2. Молекулалар немесе ауқымды құрылымды масштабтағы жағдайлар

3.Физикалық және химиялық процестер

4.Аралас физикалық және химиялық процестер

5.Аппарат масштабында макродинамикалық ортаны анықтайтын процестер жиыны.

Мұндай талқылау бүкіл процестің жағдайын және олардың арасындағы байланыстар жиынын толық орнатуға мүмкіндік береді.

Математикалық модель арқылы объектінің қасиеттерін үйрену математикалық модельдеу деп аталады. Процес өтуінің тиімді шарттарын анықтау, математикалық модель негізінде оны басқару және обьектінің нәтижелерін алу оның мақсаты болып табылады.

Математикалық модельдеу дегенде – берілген нақты обьектінің кейбір математикалық обьектіге сәйкестігін белгілеу кезеңі түсініледі. Бұл математикалық обьект математикалық модель деп аталады және бұл модельді құру үйреніліп жатқан нақты обьект сипаттамаларын алу мүмкіндігін береді.

Матемаикалық модельдің түрі тек қана обьекттің табиғатына байланысты болып қоймастан, обьектті құру мәселелеріне, талап етілген сенімділік және бұл мәселені шешу дәлдігіне байланысты болады. Әр қандай математикалық модель нақты процеске жақындық дәрежесімен нақты обьект үшін математикалық модельдеудің аналитикалы, имитациялық және олардың комбинациясы корініснде болуы мүмкін.

Математикалық модель түсінігі модельдеу тәсілінің негізгі түсініктемелері болып табылады. Математикалық модел деп математикалық белгілеу арқылы берілетін, қандай да бір жағдай немесе сыртқы әсердің жуық көрінісіндегі берілуіне айтылады.

Математикалық модельдеу үш деңгейден тұрады [2]:

1) Зерттейтін объектінің математикалық теңдеуін құру

2) Математикалық теңдеулер жүйесін шешу тәсілін таңдау және модельдеуші бағдарлама формасында оны жариялау

3) Модельдің объектіге сәйкестігін ,адекваттығын анықтау.

Математикалық модельді құру кезеңінде объектегі негізгі жағдайларды және элементтерді алдын ажыратып алады, кейін олар арасындағы байланыстар анықталады. Кейін, әр бір ажыратылып алынған элемент және жағдай үшін функциялануын көрсететін математикалық теңдеу (немесе теңдеулер жүйесі) жазылады. Бұдан басқа, математикалық түрдегі түрлі ажыратып алынған жағдайлар арасындағы байланыс теңдеулері жүргізіледі. Процестің математикалық жазылу түріне қарап, алгебралық, дифференциалдық, интегралдық және интегро-дифференциалдық жүйелер деп бөлінеді.

Шешу тәсілін таңдау және модельдеу бағдарламасын жасап шығу кезеңі бар болған әдістер ішінен ең тиімді шешу әдісін таңдауды назарға алынады, және алдын шешу алгоритмі, кейін ЭЕМ де бағдарламасы жасалынады.

Тәжірибе жүзінде математикалық модельдің сәйкестігін тексеру үшін процесс кезінде объектіден алынған өлшеулер нәтижесінің ұқсас жағдайдағы модель нәтижелері мен салыстыру қажет.

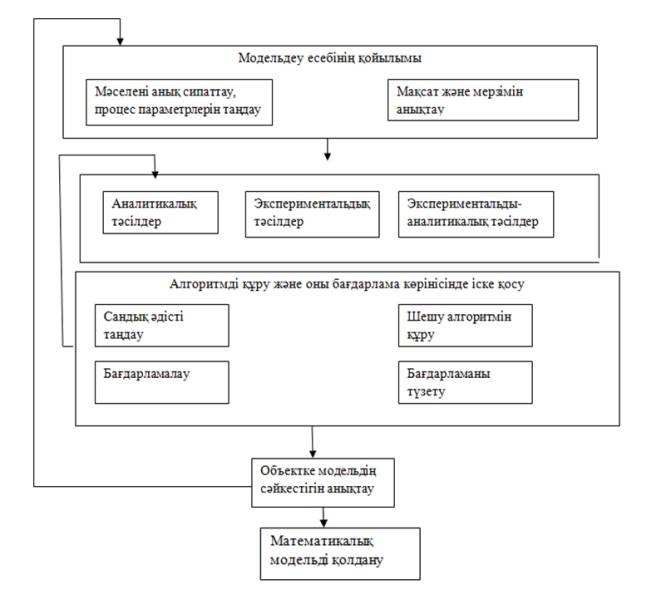
1-Сурет. Математикалық модельді жасаудың жалпы сұлбасы

Модельдің сәйкестігін (адекваттығын) жасау кезеңі оны өндіріс кезеңдерінің реттілігі мен жақын келуі болып есептеледі. Суретте математикалық модельді жасаудың жалпы сұлбасы көрсетілген.

Математикалық модель құруда нақты жағдайлар қарапайым жағдайларға келтіріледі, схемасы жасалынады және алынған схема жағдайдың күрделілігіне байланысты анау немесе мынау кезеңде математикалық аппарат жәрдемінде көрсетіледі.

Ендірілген модельдің сәйкестігі және одан алынған нәтижелердің пайдалылығы модельмен зерттелініп жатырған процестің мінездемесі және қасиеттерінің есебінен дұрыс алынғандығына байланысты болады[3].

1) Процеске әсер ететін барлық ең қажетті нәрселер модельде есепке алынған болуы және сонымен бірге екінші дәрежелі нәрселермен тізбектелген болуы мүмкін, оларды есепке алу тек қана математикалық теңдеуді түрлендіреді және модельді жалпы іске аспайтын дәрежеге келтіруі мүмкін.

Математикалық көрінісінің күрделілігіне қарап, екі шекаралық жағдайды ажырату мүмкін:

1) Модельденіп жатқан процестің барлық негізгі жақтарын көрсететін теңдеулердің толық жүйесі және бұл теңдеулердің барлық сандық мәндері белгілі

2) Процестің толық математикалық көрінісі жоқ

Бұл екінші жағдай обьект туралы толық ақпарат болмаған жағдайда процесті басқару жағдайы болып табылады.

Сондықтан модель арқылы өткізілген тәжірібиелер нәтижелерін процестермен салыстыру қажет.

Өндірістегі модельдеу объектілері деп төмендегілерді түсіндіру керек:

1. Технологиялық жүйелер (ТЖ) – бұл технологиялық құрылымдардың бөлшектері автоматтандырылған желілер, сәйкестендірілген өндіріс жүйелері (СӨЖ);

2. Технологиялық процесстер (ТП);

3. Технологиялық құрылғылар жұмыс істеп жатқан кезде, пайда болатын физикалық және химиялық процесстер (ФХП);

Модельдеу процесіне екі негізгі талап қойылады:

Біріншіден, модельдегі эксперимент оригиналдағы экспериментке салыстырғанда қарапайым және қауіпсіз болуы қажет.

Екіншіден, модельді сынау негізінде оригиналдың параметрлерін есептеуде қолданылатын қағида бізге белгілі болуы қажет. Онсыз ең жақсы модельдеуде пайдасыз болып қалады.

Таза көріністе берілген объекттің математикалық модельдері аз қолданылады, олар комбинацияланған. Мәселен ТЖ математикалық модельдерінде ТБ математикалық модельдерінен пайдаланылады, оларда өз кезегінде ФХП математикалық модельдерінен пайдаланылады.

Математикалық модельдеуде компьютерлердің кең қолданылуы, құрылған теория және алынған елеулі практикалық нәтижелер есептеу экспериментін ғылыми және қолданбалы зерттеулердегі жаңа технология мен әдістеме деп атауға болады.

Есептеу экспериментінің натуралық эксперименттерден артықшылық жақтарына тоқтала кетейік. Әдетте, есептеу эксперименті физикалық эксперименттен арзан болады. Бұл экспериментке жеңіл және қауіпсіз араласуға болады. Оны бірнеше рет қайталауға болады, сондай-ақ кез келген уақытта тоқтатуға болады. Эксперимент кезінде лабораториялық жағдайда келтіріп шығару мүмкін болмаған жағдайларды модельдеу мүмкін. Есептеу экспериментінің негізгі кемшілігі оның нәтижелерін қолдану мүмкіншілігі қабылданған математикалық модель шеңберінде ғана болады.

Әдебиеттер

1. Кафаров В.В., Перов В.А., Мешалкин В.П. Принципы математического моделирования химико-технологических систем. - М.,  Химия, 1976.

2. Хартман К., Лецкий Э., Шефер В. и др. Планирование эксперимента в исследовании технологических процессов. – М., Мир, 1977.

3. Бадалов Ф.Б. Теория оптимизации математическое програмирование "Уқитувчи" Т. 1988 г.

Алматинский технологический университет

Кафедра Информационные технологии

Айтбаева Рахатай Бекбергеновна

г.Алматы Толе би 100

rakhatay@mail.ru, 87476996636