Математика/5. Математическое моделирование

Бақытжан Д.Ә.

Гимназия №105 им. У.Джандосова», г. Алматы, Казахстан

«Алгоритм Бакытжан» для решения общей целочисленной

задачи линейного программирования

АННОТАЦИЯ

В работе построен довольно быстро сходящийся алгоритм решения общей целочисленной задачи линейного программирования, для решения которой практически не существовало известных и эффективно реализуемых методов.

В работе приводится, разработанный автором индивидуально, алгоритм решения общей целочисленной задачи линейного программирования. Данный алгоритм состоит из двух этапов, каждый из которых состоит из последовательности нескольких шагов. На первом этапе по определенным законам находится разрешающий элемент, по которому в дальнейшем, на втором этапе, проводится преобразование, переводящее предыдущее условно-оптимальное решение задачи в последующее, также условно-оптимальное, решение. В работе доказано, что условно-оптимальное решение при выполнении всех ограничений задачи есть оптимальное решение задачи. Построенный алгоритм имеет довольно хорошую сходимость, так как на каждой итерации алгоритма происходит уменьшение всех значений , нижней границей которых есть значение «ноль».

Актуальность проблемы. Задачи линейного программирования и ее модификации часто возникают в экономике, прикладной математике, технике, биологии, генетике, транспорте и т.д., что характеризует актуальность проблемы.

Во многих практических задачах линейного программирования, по самому смыслу задачи, требуется, чтобы решение было целочисленным. Однако, почти все известные оптимальные методы решения задачи линейного программирования не приводят к целочисленному решению. Поэтому разработка эффективных и оптимальных методов решения целочисленных задач линейного программирования является довольно актуальной проблемой, [1].

§1. Постановка задачи

Найти наибольшее значение функции

Z = 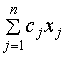(1)

при ограничениях:

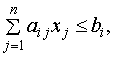
=1,2,…, m; (2)

0 ≤ ≤ ,j = 1,2,…, n (3)

Примечание 1. Задача на нахождение минимума функции (1) сводится к задаче на максимум, если поменять все знаки у коэффициентов на противоположные.

Примечание 2. Если в системе (2) есть неравенства вида AXB, то они, умножением обеих частей неравенств на «-1», приводятся к виду -AXB.

Ввожу следующие понятия.

1. Каждому столбцу jсоответствует основной вектор, состоящий из следующих трех компонент:

, j = 1,2,…, n; и (4)

2. Каждой паре столбцов j и j_о , удовлетворяющих условию

0 , (5)

соответствует простой субвектор с компонентами:

= - , =1,2,…, m; - и = (6)

3. Каждой паре столбцов j и j_о , удовлетворяющих условию

0 и , (7)

соответствует парный субвектор с компонентами:

=, =1,2,…, m; и = (8)

4. Разность двух векторов, среди которых есть какой либо субвектор, первые компоненты которых есть, например, и , если имеет место представляет собой сложный субвектор с первой компонентой

= (9)

Выражение (9), а также первые компоненты выражений (6) и (8), которые в общем виде можно записать как

, (10)

называю алгеброй этого субвектора.

Вторые и третьи компоненты этих сложных субвекторов вычисляются по формулам, аналогичным формулам (6), (8) и (9).

5. Третьи компоненты всех векторов называются оценками этих векторов.

Определение 1. Все вектора с алгеброй вида (10) называются допустимыми векторами (субвекторами) по строке , если:

_j; 0_jпри _j 0;

_j; при _j 0;

_j; при _j 0;

_j; и _j при _j 0;

Определение 2. Вектор столбца j называется допустимым вектором (субвектором), если он допустим по столбцу jдля всех строк =1,2,…, m.

§2. Алгоритм метода.

Алгоритм состоит из двух этапов. Первый этап состоит в нахождении разрешающего вектора. Второй этап заключается в построении оптимального решения задачи (1) – (3).

Э т а п 1.

Шаг 0. В каждом столбце j создается основной вектор согласно формуле (4). Каждой паре столбцов j и j_о , удовлетворяющих условию (7), ставится в соответствие новый столбец, у которого устанавливается парный субвектор с компонентами вида (8).

Создается вектор Х. Устанавливаются:

Шаг 1. Находится строка с наименьшим значением . Если 0, то выполняется шаг 4, иначе – шаг 2.

Шаг 2. Проверяется, есть ли в строке вектор с компонентой Если такого вектора нет, то задача решения не имеет. Выполняется шаг 3.

Шаг 3. В строке среди всех векторов, для которых отыскивается допустимый вектор с наименьшей оценкой. Найденный вектор принимается как разрешающий.

Переходим на шаг 6.

Шаг 4. Проверяется, есть ли в строке допустимый вектор с компонентой Если есть, то выполняется шаг 3, иначе – шаг 5.

Шаг 5. В строке среди допустимых выбирается разрешающий вектор по наибольшей оценке.

Примечание 3. Если в качестве разрешающего вектора на шагах 3 и 5 этапа 1 выбран субвектор с алгеброй А и значением сто на следующей итерации противоположный субвектор с алгеброй «-А» считается недопустимым.

Шаг 6. Если разрешающего вектора (субвектора) нет (они все недопустимы), то задача решена, и значения вектора Xи Z дадут ответ задачи. В противном случае переходим на этап 2.

Э т а п 2.

Шаг 1. Сортировка разрешающего вектора (субвектора). Если разрешающий вектор есть основной вектор, то выполняется шаг 2, если парный субвектор – шаг 4, простой субвектор – шаг 6, сложный субвектор – шаг 7.

Шаг 2. Значение соответствующее разрешающему вектору, увеличивается на единицу. Устанавливаются:

(11)

Шаг 3. Фиксируется строка с наименьшим значением Во всех клетках () этой строки, для которых устанавливаются простые субвектора (при повторении комбинации, т.е. если алгебра вектора есть в базе, субвектор не устанавливается) с компонентами:

(12)

Все вектора проверяются на допустимость. Недопустимые вектора стираются. Алгебра вектора заносится в базу. Выполняется шаг 1 этапа 1.

Шаг 4. Пусть разрешающий вектор соответствует парному субвектору с компонентами (8). Тогда значения и увеличиваются на единицу.

Устанавливаются значения и по формулам, аналогичным формулам (11).

Шаг 5. Пусть компоненты парного субвектора соответствуют формулам (8). Тогда по столбцу , при условии что , устанавливается сложный субвектор (если его нет в базе) с компонентами:

= - , =1,2,…, m; = - ; = /

Устанавливаемый субвектор проверяется на допустимость. Недопустимый субвектор стирается. Алгебра вектора заносится в базу.

Выполняется шаг 1 этапа 1.

Шаг 6. Пусть выбор пал на простой субвектор, тогда величинаувеличивается, а величина уменьшается на единицу.

Устанавливаются значения и Z по формулам (11).

Выполняется шаг 8.

Шаг 7. Пусть выбор пал на сложный субвекторкомпонента которого имеет вид (10). Тогда значения при 0 уменьшаются на величину ; значенияпри 0 увеличиваются на величину .

Устанавливаются новые значения и Z по формулам, соответствующим формулам (11).

Шаг 8. Фиксируется строка с наименьшим значением . Во всех клетках этой строки, где для субвекторов выполняются условия:

устанавливаются, если его нет в базе, сложные субвектора с параметрами:

при условии, что они окажутся допустимыми.

У каждого создаваемого вектора вычисляются оценки по формуле b. Все вектора проверяются на допустимость. Недопустимые вектора стираются. Алгебра вектора заносится в базу.

Принимаем:Выполняется шаг 1 этапа 1..

Алгоритм закончен.

Примечание 4. Для всех образованных субвекторов, наряду с их числовым значением сохраняется и их алгебраическое выражение, заданное формулами (6), (8) – (10). Алгебра хранится в базе и повторно ее выражение не устанавливается.

3. Оптимальность и конечность алгоритма

Определение 3. Вектор = есть условно-оптимальное решение задачи (1)-(3), если оно оптимальное при заданных измененных значениях

Теорема оптимальности. Пусть вектор есть условно-оптимальное решение задачи (1)-(3) и оценка

(13)

где (14)

тогда вектор (15)

с положительной компонентой соответствующего разрешающего вектора, также есть условно-оптимальное решение задачи (1) – (3) при

i=1,2,…m (16)

Доказательство. Пусть Z() есть значение целевой функции (1) для условно-оптимального решения . Тогда

(17)

Если то из (13) вытекает, что значение функции (17)для индекса будет больше значения этой функции для индекса j. Таким образом, вектор (15) есть условно-оптимальное решение при определяемых

по формуле (16). Если то на основании (13), учитывая что

(18)

для индекса i, удовлетворяющем условию (14), заключаем: вектор (15) есть

условно-оптимальное решение задачи (1)-(3) при значениях определяемых поформуле (16). В этом случае, очевидно, что увеличение j-той компоненты вектора на единицу, делает вектор недопустимым.

Присоответствующего вектора не существует.

Теорема доказана.

Далее, нетрудно видеть, что теорема оптимальности, доказанная при положительном значении компоненты у разрешающего вектора, справедлива и при

Действительно, если компонента разрешающего вектора положительна, то на основании шага 3 этапа 1 в качестве разрешающего будет выбран вектор с наибольшим значением (для этого варианта оценка вектора будет наименьшей, так как она отрицательна) и этот случай сведется к доказанной теореме оптимальности.

Если компонента у разрешающего вектора отрицательная, то, опять на основании шага 3 этапа 1, в качестве разрешающего будет выбран вектор с наименьшей оценкой, т.е. будет выбран вектор с наибольшим значением

( Нетрудно видеть, что в этом случае будет действовать обратный вариант теоремы оптимальности, т.е. вариант, когда будет меньше значения .

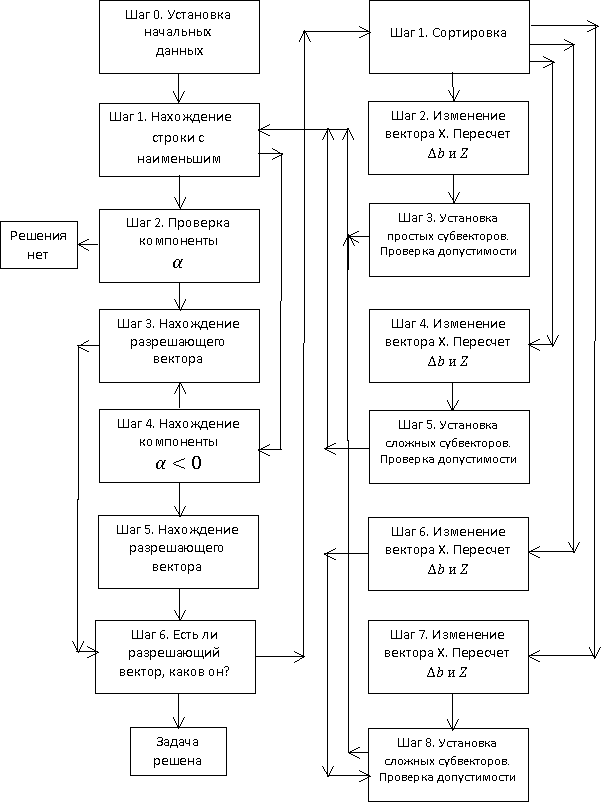
Общая схема «Алгоритма Бакытжан»

Этап 1 Этап 2

Теорема оптимальности будет справедлива и в этом случае. Тут надо учесть, что уменьшение значения функции происходит при сокращении значения (в виду того, что т.е. условная оптимальность решения (15) сохраняется.

Итак, на основании этой теоремы каждая итерация алгоритма переводит одно условно-оптимальное решение задачи в другое условно-оптимальное решение, каждый раз сокращая значения на величинуi=1,2,…m. И, как только значение для индекса, удовлетворяющего условию (14), окажется меньше всехi=1,2,…n,оставаясь при этом неотрицательным числом, будет получено оптимальное решение. В этом случае все вектора окажутся недопустимыми.

Конечность алгоритма гарантирована тем, что значения, вначале равные каждый раз уменьшаются на величинуоставаясь при этом положительным числом.

Список использованной литературы

1. Шанкибаев Б.Н. Новые подходы к решению задач целочисленного программирования. Алматы, 2009, 148 стр.

2. Бақытжан Д.Ә. Алгоритм решения общей целочисленной задачи линейного программирования. ІЗДЕНIC – ПОИСК. Международный научный журнал – приложение РК. Серия естественных и технических наук: ISSN-1560-1730, №3(1)/2015, Алматы, 2015, с. 195-201.

3. Бақытжан Д.Ә. Шаговый метод решения задачи «о ранце». Свидетельство ИС 0015977 о Государственной регистрации прав на объект авторского права № 896 от 19 мая 2015 г.

4. Бақытжан Д.Ә. Шаговый алгоритм решения общей целочисленной задачи линейного программирования. Свидетельство ИС 002041 о Государственной регистрации прав на объект авторского права № 1279 от 25 июня 2015 г.

5. Бақытжан Д.Ә. Решение многомерной задачи «о ранце». Доклад на Международной научной конференции XII nternational Research and practice conference «TRENDSOFMODERNSCIENCE», г. Шеффильд, Англия, 30 мая – 07 июня 2015 г.