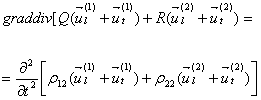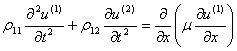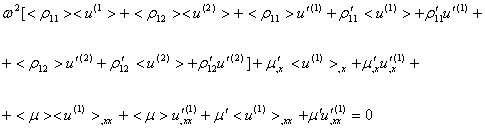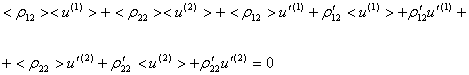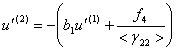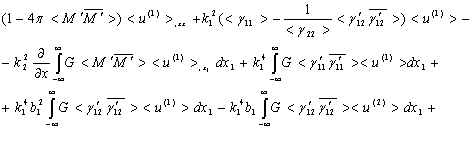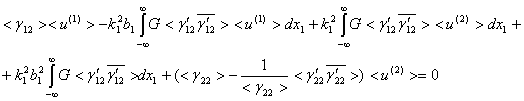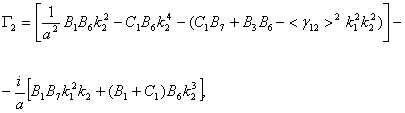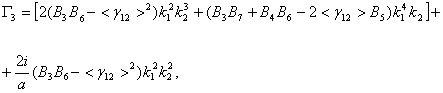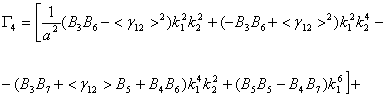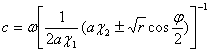MOLECULAR PHYSICS
Д.ф.м.н. Поленов В.С.
Воронежский институт экономики и права, Россия
ДИНАМИЧЕСКОЕ ДЕФОРМИРОВАНИЕ СТОХАСТИЧЕСКИ
НЕОДНОРОДНЫХ ДВУХКОМПОНЕНТНЫХ СРЕД
Изучается одномерная
модель двухкомпонентной стохастически неоднородной среды, одна компонента
которой представляет твердую среду (скелет упругой среды), а вторая – сжимаемая
жидкость. Предполагается, что в такой среде распространяются поперечные волны.
Для заданной величины дисперсии получены аналитические выражения, определяющие
скорость и коэффициент затухания поперечной волны. Показано влияние
неоднородности среды на коэффициент затухания и скорость распространения волны.
Построены графики зависимости коэффициента затухания поперечной волны от
частоты при заданных значениях математического ожидания модуля упругости и плотности
пористой среды.
В работах [1-2] рассматривались задачи о
распространении продольных и поперечных волн в однокомпонентной среде.
Предполагалось, что среда является неограниченной, изотропной и стохастически
неоднородной.
1.
Постановка задачи. Динамическое поведение
неоднородных упругих двух-компонентных сред, в векторной форме описывается
системой уравнений [3-5]
|
|
(1.1) |
где 
оператор Лапласа; 
вектор перемещения твердой компоненты; 
вектор перемещения жидкости; 
модули упругости Ламэ; 
коэффициенты, зависящие от пористости твердой компоненты
(пористого скелета), истинного модуля сжимаемости твердой компоненты и модуля
сжимаемости жидкости; 
и 
массы твердой компоненты и жидкости в единице объема
среды; 
коэффициент динамической связи твердой компоненты и жидкости.
Все параметры пористой среды являются функциями пространственных координат.
Индексы, стоящие вверху в круглых скобках, относятся: 1- к твердой компоненте,
2 - к жидкости.
Представим векторы перемещения 
и 
в виде суммы двух
составляющих
|
|
(1.2) |
где слагаемая 
удовлетворяет условию
|
|
(1.3) |
а слагаемая 
условию
|
|
(1.4) |
где 
вектор перемещения продольной волны; 
вектор перемещения поперечной волны.
При подстановке (1.2) в систему уравнений (1.1)
получим
|
|
(1.5) |
Применяя сначала к обеим частям равенства
(1.5) операцию 
и принимая во
внимание условие (1.3) и что 
, получим
|
|
(1.6) |
Аналогично применяя к системе (1.5)
операцию 
, и принимая во внимание условие (1.4) и что 
, находим
|
|
(1.7) |
Системы (1.6) и (1.7) описывают
распространение продольных и поперечных упругих волн в неоднородной
двухкомпонентной среде.
2.
Поперечные волны. Рассмотрим систему
(1.7) для одномерного случая и запишем ее в виде (индекс 
опущен)
|
|
(2.1) |
где 
модуль сдвига, 
коэффициент динамической связи упругой компоненты и
жидкости, 
эффективные массы
упругой компоненты и жидкости; 
плотности компонент. Параметры, описывающие данную среду,
являются случайными функциями координаты
Представим 
, 
в виде суммы
математического ожидания и флуктуации
|
|
(2.2) |
Символ < > обозначает
математическое ожидание соответствующих фун-кций, штрих–их флуктуации.
Система (2.1) с учетом (2.2) и зависимости
перемещений компонент от времени при помощи множителя 
будет записана в виде
|
|
(2.3) |
|
|
|
Осредним
выражения (2.3) и из (2.3) вычтем осредненное , получим систему
уравнений относительно средних перемещений
|
|
(2.4) |
и относительно флуктуаций
|
|
(2.5) |
В формулах (2.4) и (2.5) введены следующие
обозначения:
|
|
(2.6) |
, 
, 
Систему (2.5) преобразуем к виду
|
|
|
|
|
|
, 
Уравнение (2.7) представляет собой
уравнение Гельмгольца, решение которого выражается через функцию Грина 
|
|
(2.9) |
которая удовлетворяет уравнению
|
|
(2.10) |
где 
функция Дирака.
Тогда (2.8) с учетом (2.9) запишем в виде
|
|
(2.11) |
Подставим (2.9) и (2.11) в правые части (2.4)
и, учитывая уравнение (2.10), получим систему дифференциальных уравнений
относительно средних перемещений компонент среды
|
|
(2.12) |
||
|
|
(2.13) |
|
|
Черта сверху над буквой обозначает
комплексно–сопряженную величину.
Решение (2.12) и (2.13) будем искать в
виде
|
|
(2.14) |
Здесь 
амплитуды волн, 
волновое комплексное число, 
мнимая единица.
Если подставить (2.14), решение функции
Грина 
и значения корреляционных
функций
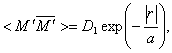
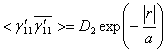
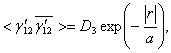
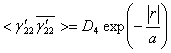
где 
дисперсии, 
радиус корреляции функции
и в соотношениях
(2.12-(2.13) сделать замену 
то получим однородную систему двух
алгебраических уравнений относительно амплитуд
и 
|
|
(2.15) |
где введены обозначения
|
|
(2.16) |
Однородная система (2.15) имеет
нетривиальное решение при условии, когда определитель системы равен нулю.
Раскрывая определитель второго порядка, составленный из коэффициентов при 
и 
получим
алгебраическое уравнение четвертой степени с комплексными коэффициентами
относительно волнового комплексного числа 
|
|
(2.17) |
|
|
|
,
Из уравнения (2.17) определим коэффициент
затухания 
и скорость 
волны по формулам [6]
|
|
(2.18) |
круговая частота.
Рассмотрим случай упругой двухкомпонентной
среды с заданной величиной дисперсии: 
В этом случае
соотношения (2.16) принимают вид
|
|
(2.19) |
Тогда уравнение (2.17) для определения
коэффициента затухания и скорости распространения поперечной волны в
стохастически неоднородной двухкомпонентной среде запишем в таком виде
|
|
(2.20) |
|
|
|
|
|
|
|
|
|
Из уравнения (2.20) находим волновое
комплексное число
|
|
(2.21) |
По формуле (2.18) определим коэффициент
затухания 
и скорость
распространения поперечной волны 
в двухкомпонентной
стохастически неоднородной пористой среде
|
|
(2.22) |
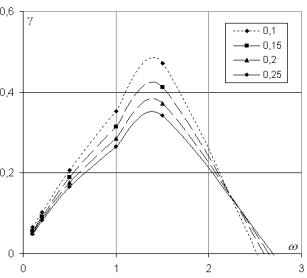
Рис. 1. Зависимость коэффициента затухания от частоты
На рис. 1. показана зависимость
коэффициента затухания распространения поперечной волны от частоты, вычисленная
по формуле (2.22) при различных значениях радиуса корреляции (неоднородность
среды), указанного на рисунке и заданных математических ожиданиях: 
Литература:
1. Чигарев А.В.
Стохастическая и регулярная динамика неоднородных сред //Минск.: Технопринт.
2000. 425 с.
2. Шуман Б.М.
Распространение упругих волн в среде со случайными неоднородностями //Прикл.
мех. Киев. 1968. Т. IV. Вып. 10. С. 6–13.
3. Biot M.A. Theory of propagation of elastic
waves in a fluid-saturated porous solid I. Low-frequency range//J. Acoust. Soc. America. 1956. V. 28. № 2. P.168
-178.
4. Косачевский
Л.Я. О распространении упругих волн в двухкомпонентных средах //ПММ. 1959.
Т. 23. Вып. 6. С. 1115 - 1123.
5. Поленов В.С.,
Чигарев А.В. Распространение волн в насыщенной жидкостью неоднородной
пористой среде //ПММ. 2010. Т. 74. Вып.2. С. 276– 284.
6. Поленов В.С.,
Чигарев А.В. Распространение волн в вязкоупругой среде со случайными
неоднородностями //Сб. Тр. НИИ мат. ВГУ. Воронеж. 1972. Вып. 6. С. 25 – 27.