УДК 622.831

Э.К. Абдылдаев д-р техн. наук, проф., Д.М. Сулейменов - магистр АТУ

Алматинский технологический университет, Казахстан

ЧИСЛЕННЫЕ ПРОЦЕДУРЫ ОЦЕНКИ ДЕФОРМИРОВАНИЯ ОТКОСОВ

В статье изложена численная процедура и результаты моделирования деформации откосов на эквивалентных материалах и на методе конечных элементов на ПК

Ведение открытых горных работ изменяет исходное напряженное состояние массива горных пород. В окрестности горных выработок в результате перераспределения напряжений нарушается установившееся состояние равновесия пород, что при определенных условиях приводит к неупругому деформированию бортов или подошвы выработки. Поэтому исследования устойчивости бортов карьеров тесно связано с изучением напряженно-деформированного состояния массива горных пород.

Многочисленными натурными наблюдениями за деформациями бортов карьеров и исследованиями деформаций откосов на моделях из эквивалентных материалов установлено, что прибортовой массив до обрушения претерпевает сложное деформирование: горизонтальное растяжение, вертикальное сжатие и сдвиг. При коэффициенте запаса устойчивости откоса, близком к предельному и напряжениях, превышающих предел ползучести горных пород, деформации развивается плавно. При моделировании откосов в процессе развития деформаций до разрушения прибортовых массивов выделяются три периода:

- начальный, соответствующей времени отстройки борта, скорости смещения в котором зависят от темпа его оформления, а по завершению оформления в течении некоторого периода носят затухающий характер ;

- период с постоянной скоростью деформирования;

- период с прогрессирующей скоростью деформирования заканчивающейся разрушением массива.

При этом накопление смещений прибортового массива за указанные периоды относительно общего смещения до разрушения происходит в соотношениях для первого периода - 45-50%, для второго - 20-25% и третьего около 30%.

Моделированием откосов на эквивалентных материалах установлены зоны распространения и концентрации деформаций. При этом значение предельных величин деформации: горизонтальных растяжений -50.10^-3, вертикальных сжатий -(40-50 )^.10^-3 , сдвигов -(80-100).10^-3. Следует отметить, что указанные величины деформации наблюдались в откосе с коэффициентом запаса устойчивости k =1.04 и находящийся в стадии пластического деформирования ; продолжительность деформирования откоса до обрушения составляла 2,5 часа. По достижению указанных величин деформации откос обрушался практически мгновенно.

После установления достоверных величин деформаций откосов моделей и размеров зон их распространения, появилась реальная возможность оценить результаты расчетов напряженно-деформированного состояния откосов, методом конечных элементов (МКЭ) на основе разработанной численной процедуры в условиях плоской деформации.

Решение линейной упругой задачи на МКЭ сводится к решению системы алгебраических уравнений, при построении который используется линейный закон связи напряжений и деформаций. Возможности МКЭ в максимальной степени раскрываются при анализе ситуаций в средах со сложными прочностными деформационными свойствами.

Пусть нелинейная связь полных напряжений и деформаций имеет вид:

{s}=[D_уп]{e} (1)

где элементы матрицы[D_уп] не являются постоянными величинами, а зависят от деформации. Эта матрица не обязательно должна быть задана в явном виде. Достаточно задать серию операций , с помощью которых по заданным деформациям {s} можно было бы вычислить теоретические напряжения в данной нелинейной среде.

Первоначально прикладывается полная заданная нагрузка, решается упругая задача с начальными, упругими свойствами. Составляется МЖС и рассчитываются напряжения и деформация. Соответствующие рассчитанным деформациям теоретические напряжения {s^т}₁, вычисленные по формуле (1), будут отличаться от упругих напряжений{s}₁. Разница

{s}₁-{s^т}₁={Ds ^н}₁, (2)

рассматривается как прирост начальных напряжений. Прирост начальных напряжений элемента пересчитывается в начальные узловые силы:

{F}= R_y ∫ _s [B]^т{Ds ^н} dS , (3)

где Ry-коэффициент ускорения сходимости.

Оптимальная величина для широкого диапазона моделей сред будет R_y=1,5.Найденные по (3) начальные узловые силы добавляются к вектору сил системы, и приводится следующее упругое решение с прежней МЖС . но с новым набором узловых сил. Следует отметить. что добавление начальных сил увеличит упругие напряжение в элементе , однако на величину меньшую. чем начальные напряжения, по которым были рассчитаны узловые силы, поскольку в ансамбле элементов добавленные начальные силы распределяются также и на другие элементы области. Вновь определяем теоретические напряжения {s}, соответствующие новым деформациям, и дополнительные начальные напряжения. Процесс продолжается до тех пор , пока найденные упругие напряжения за вычетом суммарных накопленных начальных {s} не станут достаточно близки к теоретическим. Для решения задач, в которых в процессе нагружения главные напряжения меняет направление, необходимо производить пошаговое нагружение и использовать модель, отвечающую принципам теории пластического течения.

Процедура получения упругопластического решения по теории пластического течения с помощью начальных напряжений такова. Нагрузка прикладывается малыми ступенями в той последовательности, в какой происходит реальное нагружение в натуре. Решения для очередного, например n-го, шага нагрузки достигается точно по выше изложенному методу начальных напряжений. К началу шага известны суммарные напряжения в элементах от (n-1) предыдущих ступений {s}_n-1.

К области прикладывается вектор сил (и заданных перемещений) очередной ступени нагрузки и в итерационном режиме повторяются упругие решения с изменяемым вектором.

В очередном 1 - м цикле итераций в элементах вычисляется прирост деформаций {De}ⁱ_n , соответствующей им упругий прирост напряжений

{Ds^y}ⁱ_n=[D]{De}ⁱ_n , (4) упругие напряжения

{s^y}ⁱ_n={s}_n-1 +{Ds^y}ⁱ_n (5)

“ Фактический “ прирост напряжений равный разности между упругим приростом и накопленными на предыдущих (n-1) циклах итерации начальными напряжениями :

{Ds^ф}ⁱ_n={Ds^y}ⁱ_n -{s^н}_n (6)

По заданной модели среды вычисляется “теоретический“ прирост напряжений {Ds^т}ⁱ_n, соответствующей приросту деформаций {De}ⁱ_n .Разность между фактическим и теоретическим приростами рассматривается как приращение начальных напряжений:

{Ds^н}ⁱ_n={Ds^ф}ⁱ_n-{Ds^т}ⁱ_n (7)

По приращению начальных напряжений и рассчитывается по формуле (3) добавка к вектору начальных сил. Начальное напряжение накапливаются цикл за циклом в пределах шага нагрузки :

{s^н}_n={s^н}_n+{Ds^н}ⁱ_n (8)

Если приращение начальных напряжений в каждом из элементов не стало достаточно мало, начинается следущее (i+1)-я итерация. Когда же необходимо точность достигнута, прикладывается следущая (n+1)-я ступень нагрузки. Необходимо отметить что, в вышеприведенных уравнениях не учитываются временной фактор.

К расчету по МКЭ приняты следующие физико-механические характеристики смеси, используемой при моделировании плотность g =3.34гс/ см³, угол внутреннего трения j=30⁰, сцепление С=5.85гс/ см², модуль упругости Е =2^.10⁵ гс/ см², коэффициент Пуассона v=0.3. Рассчитывая откос с углом наклона 45⁰ и высотой 64 см с коэффициентом запаса устойчивости k= 1.02.

Рассмотрим нетронутый (свежесформированный, как это имеет место при моделировании) массив. Перемещение в свежесформированном массиве под влиянием веса возможны только в вертикальном направлении. Оформление откоса изменяет сформировавшееся поле напряжений в нетронутом массиве. Выемка и удаление определенной массы при оформление откоса вызовет прежде всего релаксации напряжений, вызывающих в массиве упругие деформации, и приведет к упругому восстановлению массива. Однако упругим восстановлением деформирования прибортового массива не заканчивается. На откос будут постоянно действовать напряжения бокового распора, которые вызывают дальнейшие процессы изменения напряженного состояния и перемещения в прибортовом массиве.

Результаты расчетов деформаций прибортового массива откоса показывают, что наибольшим смещением подвергаются точки верхние бровки откоса и часть массива прилегающая к контуру откоса. Зона концентрации горизонтальных и вертикальных деформаций наблюдаются в средней части ближе к поверхности откоса. Анализ деформации сдвигов дает, что зоны концентрации наблюдаются в двух местах: на верхнем бровке откоса и вблизи угла подошвы откоса. Качественная картина зоны концентрации деформаций, расположение изолинии построенных на основе моделирования эквивалентных материалов и на МКЭ подобны.

Рассчитанные параметры деформаций и перемещений прибортового массива - максимальные смещения порядка 12мм, горизонтальные деформации -25^.10^-3, вертикальные деформации -(20-25)^.10^-3, сдвиги -70^.10^-3 близки по величине к результатам полученным в процессе моделирования откосов на эквивалентных материалах. Проведенные исследования свидетельствует о достоверности разработанных численных процедур и расчетных данных МКЭ (рис.1 и рис.2).

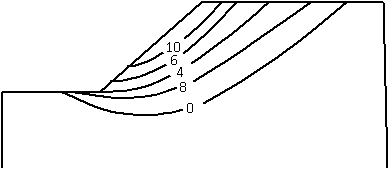
Рисунок 1 – Изолинии критических абсолютных смещений прибортового массива откоса по результатам лабораторного моделирования

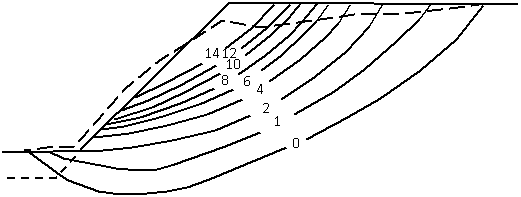
Рисунок 2 – Изолинии расчетных предельных абсолютных смещений по результатам МКЭ

СПИСОК ЛитературЫ

1. Абдылдаев Э.К. Напряженно-деформированное состояние массива горных пород вблизи выработок. - Фрунзе: Илим, 1990,-164 с.

2. Абдылдаев Э.К., Заурбекова Н.Ж., Айтуганова Ж.Т., Сулейменов Д.М. Информационная технология при моделировании задачи горного дела. Вестник Алматинского технологического университета, Алматы.-2015.- №2 (107).-С.8 -13