Pil E.A.

Russia, Saint-Petersburg

Academic of the RANH, Dr.S. (eng.). Professor,

Options OF CALCULATING VOLUME OF THE ECONOMIC SHELL

This article describes an economic shell that can be presented in the form of volume of a sphere. This volume can be presented as the gross domestic product (GDP) of a country. The types of sphere deformation are shown under the effect of external and internal pressure.

Previously, the author showed in his articles that GDP of any country can be presented as a spherical shell or, more precisely, as the area of its surface [1, 2, 3].

Gross domestic product is a macroeconomic indicator that reflects the market value of all final goods and services produced for consumption, export and accumulation in all economic sectors within the borders of a country during a year irrespective of a national identity of the used production factors. That is, it can be presented as a package of final goods and services of enterprises (companies) and, consequently, each enterprise (company) constitutes its separate part of the sphere volume.

For this purpose, the volume of an economic sphere can be categorized into two classes (Figure 1):

1. the first class - the volume of the economic sphere is a closed sphere without cracks V_sc;

2. the second class – the volume of the economic sphere is an open sphere V_so where at least two sides of two pyramids are out of contact with each other, that is, there is a crack.

Each class is further divided into the following ten equal subclasses:

1. The plotted volume of the economic sphere V_s is an aggregate of separate identical pyramids of the same volume V_pi and radius R_pi;

2. The plotted volume of the economic sphere V_s is an aggregate of separate identical pyramids of different volume V_pi and with the same radius R_si;

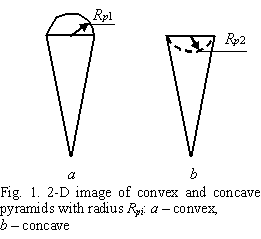
3. The plotted volume of the economic sphere V_s is an aggregate of separate, convex and concave identical pyramids of the same volume V_pi and with constant radiuses R_pi for convex R_p1 and concave R_p2 pyramids. Figure 1 represents two flat images of a convex pyramid and a concave pyramid.

4. The plotted volume of the economic sphere V_s is aggregate of separate a convex and concave identical pyramids of the same volume V_pi and with constant and varying radiuses R_pi (constant radius R_p1 is for convex pyramids and varying radiuses R_p2 are for concave pyramids).

5. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of the same volume V_pi and with constant and varying radiuses R_pi (varying radiuses R_p1 are for convex pyramids and constant radius R_p2 is for concave pyramids).

6. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of the same volume V_pi and with varying radiuses R_pi (varying radiuses R_p1 are for pyramids and constant radius R_s2 is for concave pyramids).

7. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of varying volumes V_pi and with the same radiuses R_pi (radius R_p1 is for convex pyramids and radius R_p2 is for concave pyramids).

8. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of varying volumes V_pi and with different radiuses R_pi (constant radius R_p1 is for convex pyramids and varying radius R_p2 is for concave pyramids).

9. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of varying volumes V_pi and with different radiuses R_pi (varying radius R_p1 is for convex pyramids and constant radius R_p2 is for concave pyramids).

10. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of varying volumes V_pi and with varying radiuses R_pi (varying radiuses R_p1 and R_p2 for convex and concave pyramids).

Let us consider the above stated subclasses individually:

Subclasses without cracks:

1. The plotted volume of the economic sphere V_s is an aggregate of separate identical pyramids of the same volume V_pi and same radius R_pi.

This subclass represents an ordinary sphere plotted from identical pyramids. The minimum number of sides of a pyramid is equal to three, i.e. n_fmin = 3, and the maximum number is equal to n_fmax, i.e. n_f = n_fmax. As we calculate the volume of a pyramid, then the number of its faces shall correspond to the number of the variables n_GDP used when calculating GDP of a country. Thus, it is possible to record the following boundaries for the number of faces of pyramid within which they can exist 3 £ n_f £ n_GDP. It should be noted that the volumes of pyramids are equal among themselves V_p1 = V_p2…= V_pi.

2. The plotted volume of the economic sphere V_s is an aggregate of separate identical pyramids of different volume V_pi and with the same radius R_pi. Thus, it is possible to records V_p1 ¹ V_p2…¹ V_pi for volumes. And the following derivation R_p1 is possible to record as the radiuses for the convex R_p1 and concave R_p2 pyramids are the same.

3. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of the same volume V_pi and with constant radiuses R_pi for convex R_p1 and concave R_p2 pyramids. In view of this, for this case it is possible to record V_p1 = V_p2…= V_pi for volumes of pyramids and R_p1 = R_p2 for their radiuses.

4. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of the same volume V_pi and with constant and varying radiuses R_pi (constant radius R_p1 is for convex pyramids and varying radiuses R_p2 are for concave pyramids). So, it is possible to record V_p1 = V_p2, R_p11 = R_p12 =…R_p1i = const and R_p21 ¹ R_p22.

5. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids with the same volumes V_pi and with constant and varying radiuses R_pi (varying radiuses R_p1 are for convex pyramids and constant radius R_p2 is for concave pyramids). In this subclass V_p1 = V_p2, R_p11 ¹ R_p12, а R_p21 = R_p22 =…R_p2i = const.

6. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of the same volume V_pi and with varying radiuses R_pi (varying radiuses R_p1 are for convex pyramids and varying radiuses R_p2 are for concave pyramids). Thus, V_p1 = V_p2, R_p11 ¹ R_p12, R_p21 ¹ R_p22.

7. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of varying volumes V_pi and with the same radiuses R_pi (radius R_p1 is for convex pyramids and radius R_p2 is for concave pyramids).

Here the radiuses for convex R_p1 and for concave R_p2 of pyramids can be divided into the following two groups:

· all radiuses of convex R_p1 and concave R_p2 pyramids are equal among them, that is R_p11 = R_p12 =…R_p1i = R_p21 = R_p22 =…R_p2j;

· all radiuses of convex R_p1 and concave R_p2 pyramids are equal among themselves only in their groups, that is R_p11 = R_p12 =…R_p1i, and R_p21 = R_p22 =…R_p2j consequently R_p1i ¹ R_{p2j i}.

8. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of varying volumes V_pi and with different radiuses R_pi (constant radius R_p1 is for convex pyramids and varying radius R_p2 is for concave pyramids). In this subclass V_s1 ¹ V_s2, R_p11 = R_p12 =…R_s1i = const and R_p21 ¹ R_p22.

9. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of varying volumes V_pi and different radiuses R_pi (varying radius R_p1 is for convex pyramids and constant radius R_p2 is for concave pyramids). In this case V_p1 ¹ V_p2, R_p11 ¹ R_p12 and R_p21 = R_p21 =…R_p2j = const.

10. The plotted volume of the economic sphere V_s is an aggregate of separate convex and concave identical pyramids of varying volumes V_pi and with varying radiuses R_pi (varying radiuses R_p1 and R_p2 are for convex and concave pyramids). In this case, it is possible to record V_p1 ¹ V_p2, R_p11 ¹ R_p12, R_p21 ¹ R_p22.

Three formulae are acceptable for calculation of the volume of the above described 10 variants of close economic sphere

1. Formula (1) is applied for the first two variants when the economic sphere is an aggregate of volumes of separated pyramids with a flat base

where: V_p1, V_p1…V_pi means the volume of separate pyramids, unit³.

The volume for convex and concave pyramids of radius R_pi is calculated under formulae 2 and 3 (Figure 2);

For convex pyramids

V_p1 = V_p11 + V_p12, (2)

where: V_p11 is the volume of the convex segment of the considered pyramid, unit³;

V_p12 is the volume of a pyramid, unit³.

For concave pyramids

V_p2 = V_p22 - V_p21, (3)

where: V_p21 is the volume of the convex segment of the considered pyramid, unit³.

V_p22 is the volume of a pyramid, unit³;

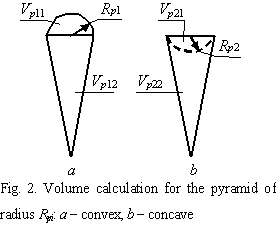
Similar descriptions are also applied to the subclass of open spheres having even one crack, that is when two faces of two pyramids are out of contact against each other.

If it is necessary to change any economic sphere from an open one, that is with a crack (cracks), into a close one, then it can be done in the following way. It is necessary to base on an equilateral single economic pyramid where its base side length l_sp is equal to one (l_sp1 = 1) and which area we indicate as S_pht1. The length of the lateral face l_f of this pyramid is also equal to unity (l_f = 1) .

On this basis, here, we will introduce a concept of “unit theoretical volume” of an economic pyramid V_pht where the length of each base side of this pyramid l_sp and the length of its lateral face l_f is equal to one, unit³. In this case, it is supposed that this pyramid has not been influenced by pressure.

Now we will perform the following transformation, we will increase (decrease) all sides of the considered pyramid depending on their sizes in such a way so that the lengths of base sides and faces are to be equal to one. Thus, we reduce all pyramids of economic shell to the unit theoretical volume V_pht1. In this case, we will receive a theoretical economic shell V_pht consisting of a set of volume units of economic pyramids V_pht1n. From this perspective, the volume of theoretical economic shell V_pht can be calculated under formula (4)

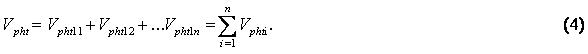
After that, we will introduce a coefficient of increase (decrease) for a base side of a pyramid l_sp and indicate it as K_sp. The application of this coefficient gives us a possibility to reduce any base side of a pyramid l_sp to be equal to unity, i.e. l_sp1 = 1, that is to equilateral polyhedron. The similar coefficient K_spb is applied for the faces of a pyramid. Thus, the values l_sp1, l_f1 and h_sp1 can be calculated under formulae 5 and 6 respectively, that means to reduce all variables of a pyramid to unity.

The value of these coefficients is always greater than zero (K_sp > 0, K_spb > 0). In this case, if the values of coefficients K_sp and K_spb are within the following boundaries 0 < K_sp < 1 and 0 < K_sbp < 1, then, consequently, the considered base side l_sp and face l_f of a pyramid are decreased as their values are more than one. If the values of coefficient K_sp and K_spb are more than one, that is K_sp > 1 and K_spb > 1, it means that a base side of a pyramid l_sp and a face l_f are within the boundaries 0 < l_sp < 1 and 0 < l_f < 1. When K_sp = K_spb = 1, it means that a base side l_sp and a face l_f of a pyramid are equal to one (l_sp = l_f = 1). In this case, definitely, there are alternatives when these coefficients have different values, for example, K_sp > 1, and K_spb < 1 or K_sp = 1 and K_spb > 1.

Since there can be a great number of pyramids in a spherical economic shell if the GDP of a country is calculated, then it is necessary to use the corresponding table which example is represented below.

Table 1. Reduction of values of all side lengths lsp and faces lf of a triangular pyramid to unity

№ п/п

lsp

Ksp

lsp

Ksp

lsp

Ksp

lf

Kspb

lf

Kspb

lf

Kspb

1

lsp11

Ksp11

lsp12

Ksp12

lsp13

Ksp13

lf11

Kspb11

lf12

Kspb12

lf13

Kspb13

2

lsp21

Ksp21

lsp22

Ksp22

lsp23

Ksp23

lf21

Kspb12

lf22

Kspb22

lf23

Kspb23

…

…

…

…

…

…

…

…

…

…

…

…

i

lspi1

Kspi1

lspi2

Kspi2

lspi3

Kspi3

lfi1

Kspbi

lfi2

Kspbi

lfi3

Kspbi

Table 1 represents an example of values reduction of all three variables in a pyramid l_sp and l_f to unity except when their values are equal to unity as in this case the coefficients will be the following: K_sp = 1 and K_spb = 1. Here a line number (serial number) (item No.) corresponds to the number of a considered pyramid.

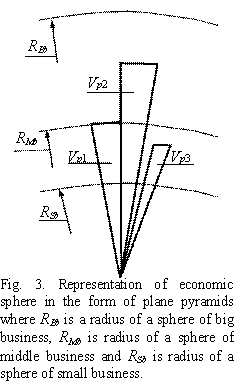
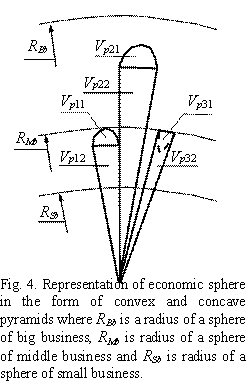
While calculating the volume of spherical economic shell, it is expedient to represent it in the form of a set of plane pyramids as it was done in Figure 3, than in the form of convex or concave pyramids represented in Figure 4. And in this case, as appears from Figures 3 and 4, these pyramids are open as pyramids 2 and 3 are out of contact against each other.

REFERENCES

1. Pil E.A. Types of deformation of economic shell under influence of various forces // Bulletin of St. Petersburg State University of engineering and economics. Series “Economy” №. 14(17), 2007 – P.226-231.

2. Pil E.A. Application of theory and shells for the purpose of description of processes taking place in economy // Almanac of modern science and education. 2009. No.3. P. 137-139.

3. Pil E.A. Influence of different variables onto economic shell of a country // Almanac of modern science and education. 2012. №. 12(67). P. 123-126.