Даулетова С.Д. , Тасибекова А.К., Алтынбеков Ш.А. - Ф-м.ғ.к., доцент, Шымкент, Қазақстан

АНЫҚТАЛМАҒАН ТЕҢДЕУЛЕРДІҢ НАҚТЫ ТҮБІРЛЕРІН ТАБУ ӘДІСІ

Қазіргі уақытта математикамен кәсіби түрде немесе әуесқойлықпен айналысқанның барлығы Диофанттық теңдеу туралы, тіпті Диофанттық анализ туралы естіген болар.Соңғы 15-20 жылдары өзінің алгебралық геометрияға жақындығына байланысты ол «сәнге» айналды.Сонымен қатар анықталмаған анализге атау берген Диофанттың өзі туралы, [1] антикалық заманның қызықты оқымыстыларының бірі туралы ештеңе айтылмаған.Оның еңбектері туралы тарихшылар өздерінің кері көзқарасына ие.Олардың көпшілігің ойынша, Диофант қу, алайда жекелеген әдістерді пайдалана отырып, анықталмаған теңдеулерге ұқсайтын жекелеген есептерді шешумен айналысқан.Осы бағалар туралы біз дәлірек төменде айтатын боламыз.

Сонымен қатар Диофант есептерін қарапайым талдау көрсетіп отырғандай,ол анықталмаған теңдеулерді сандарда шешу мәселесін қойып қана қойған жоқ және де оларды шешудің кейбір жалпы әдістерін берді.Осы орайда айта кету керек, антикалық математикада жалпы әдістер ешқашан шешілетін есептерден бөлек «таза түрінде» сипатталмаған. Диофнтпен де жағдай осыған ұқсап тұр.Виет пен Ферма үшін оның әдістері түсінікті болды және олар жаңа есептерді шешу үшін оларды пайдаланады. [1]

Диофант идеяларының дамуы Анри Пуанкаре мен Андре Вейльдің жұмыстарына дейін жалғасты.Сондықтан Диофант анализінің тарихы ерекше қызықты.

Бұл ғылыми жұмыста анықталмаған теңдеулердің түбірлерін табу әдістері қарастырылып мысалдар келтірілді.

1 - Мысал. x+y+z=0 теңдеудің [-1;1] кесіндіде неше бүтін түбірі бар?

Осы түбірлерді табыңыз.

Шешіуі. Кесіндіде үш (-1;0;1) бүтін сан болғандықтан, орналастыру теоремасына i=3 сәйкес (P₃=3!=6) теңдеудің алты бүтін шешімі бар: (-1;0;1), (-1;1;0), (0;-1;1), (0;1;-1), (1;-1;0), (1;0;-1).

2-Мысал. х³+y³+z³=2 теңдеуінің шексіз көп шешімдері болатынын дәлелде.

Шешімі: x=a + b, y=a-b ауыстыруы арқылы теңдеуді 2a³+6ab²+z³=2 түріне келтіріп a=1деп алсақ z³=-6b² → z=-6c → b²=36c² → c=β² → x=1+6β³, y=1-6β³, z=- 6β³, β – кез келген сан.[2]

3-Мысал. x₁+x₂+…+x_n+...=1 теңдеудің бірден бір оң нақты түбірлерін табыңыз.

Шешуі. Белгісіздер саны шексіз болғандықтан, есептің шартына сәйкес бұл түбірлерді табу үшін (теңдеуді шешу үшін) шексіз кемімелі геометриялық прогрецияны қолданамыз.

Ол үшін өткенімізді шолып

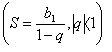теңдеудің екі жағын талдаймыз

Өткеніміз бізге жол сілтейді: х₁=

S=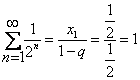

Ендеше жауабы:

4-Мысал 6х²+5у²=74 теңдеуінің шешімін тап.

Шешімі: Берілген теңдеуді 6(x²-4)=5(10-y²) түріне келтірейік. Бұдан x²-4=5u, 10-y²=6v немесе u=v болуы тура →u, v айнымалылары үшін 0 және 1-ге тең болатын екі ғана мүмкіндік бар. u=v=0 болса теңдеудің шешімі жоқ u=v=0 кезде бұдан (3;2),(3;-2),(-3;2),(-3;-2) шешімдерін аламыз.

5-Мысал x₁∙x₂∙x₃∙∙∙x_n∙∙∙= теңдеудің бірден бір нақты түбірлелін табыңыз. Шешуі. Берілген теңдеудің екі жағын талдау, теңдеуді шешу үшін бізді қысқаша көбейту формулаларына алып келеді. Себебі өзге жолы жоқ.

Теңдеудің оң жағында тұрған сан, түбірлерді бөлшек түрінде ізде деп тұрғандай. Бұл жағдайда мына формулаларды:

1. ɑ²-b²=(ɑ-b)(ɑ+b)

2. (ɑ+b)²=ɑ²+2ɑb + b²

3. (ɑ-b)²=ɑ²-2ɑb + b²

4. (ɑ+b)³=ɑ³+3ɑ²b+3ɑb²+b³

5. (ɑ-b)³=ɑ³-3ɑ²b+3ɑb²-b³

қолдану тиімсіз. Олай болса қалған екі формуланы қолданамыз

6. ɑ³+b³=(ɑ+b)(ɑ²-ɑb+b²)

7. ɑ³-b³=(ɑ-b)(ɑ²+ɑb+b²)

Қолданып көрейік. Теңдеудің оң жағында тұрған санның алымы бөлімінен кіші болғандықтан, ізделінді түбірлердің алымы да бөлімінен кіші болып келеді.[3]

Cондықтан, ізделінді түбірлерді 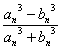түрінде іздестіреміз.

Осыдан теңдеудің оң жағында сан тұрғандықтан, көбейту барысында өрнектер қысқарып, нәтиже саны келіп шығатын ɑ_n және b_n –ді таңдаймыз. Формулаларға және сандардың қысқаруы ережелеріне сәйкес ɑ_n=n, b_n=1деп таңдасақ

Сонымен, жауабы:

ӘДЕБИЕТТЕР

1. И.Г.Башмакова ‹‹Диофант и Диофантовы уравнения›› Москва, 1972г.

2. Цыпкин А.Г. Справочник по математике для средней школы М: Наука. 1980г.

3. Бейсеков Ж. Рахымбек Д. Шарипов Т.А. Орта мектепте математиканы оқытудың әдістемесіне арналған оқу құралы.-Шымкент, 2003.-180б