УДК 69.059.25

Копец К. К.

Луганский национальный аграрный университет, Украина

Декомпозиция процесса тепломассопереноса в

подсистемах теплогенерирующих установок

В статье рассмотрена концепция динамической декомпозиции теплогенерирующих установок, предложен обобщенный показатель и показана методика его использования для упрощения математической модели системы регулирования температуры теплоносителя

Ключевые слова: тепломассоперенос, декомпозиция, температура, регуляторы.

This paper describes the concept of dynamic decomposition of heatgeneration plants, the composite index and the method of its use to simplify the mathematical model of the system of temperature control also proposed

Key words: heat and mass transfer, decomposition, temperature, controllers.

Математические модели процессов, протекающих в теплогенерирующих установках (ТГУ), представляют собой достаточно сложную систему нелинейных дифференциальных уравнений [1], включающую: математическую модель объекта регулирования (чаще всего систему нелинейных дифференциальных уравнений или уравнений в частных производных); математическую модель регулятора, включающего датчик регулируемой величины, преобразователь, собственно регулятор; модели исполнительного механизма и регулирующего органа, линий связи.

Исследование динамики процессов регулирования, оптимизацию настроек параметров регулятора целесообразно проводить на упрощенной модели, если такая возможность имеется. При оценке возможности упрощения математической модели во внимание должны приниматься погрешности идентификации параметров передаточных функций, входного сигнала, частотных характеристик и т.д. Упрощение математических моделей отдельных звеньев можно выполнить с помощью методов теории чувствительности [2].

Динамические свойства элементов теплогенерирующей установки (постоянные времени, времена транспортного запаздывания, частотные характеристики и т.п.) могут существенно отличаться. В связи с этим появляется возможность декомпозиции ТГУ на отдельные подсистемы, каждая из которых объединяет элементы, близкие по динамическим свойствам [3].

Динамическая декомпозиция основывается на концепции так называемого модельного подхода. Если Δy = Δy(t) и динамические характеристики двух подсистем теплогенерирующей установки существенно различны, то переходные процессы в них можно подразделить на быстрые и длительные. Очевидно, что в этом случае достижение нового стационарного состояния всей системой определяется длительным переходным процессом. В связи с этим при рассмотрении нестационарного поведения всей системы можно пренебречь динамикой быстрого процесса [4].

Для решения задачи динамической декомпозиции ТГУ в общем случае требуется исследовать некоторый набор динамических свойств каждого из входящих в ее состав элементов. Эта задача может оказаться весьма сложной и трудоемкой. Для ее упрощения используется показатель С_п, имеющий вид [3]

где T_ip и T_jp - динамический показатель i-ой и j-ой подсистем;

a_p=+1, если р-й показатель характеризует постоянную времени запаздывания или длительность запаздывания;

а_р = -1, если р-й показатель характеризует постоянную времени

предварения.

Обобщенный показатель позволяет осуществить декомпозицию линейных апериодических подсистем. При этом можно пользоваться следующим сопоставлением динамических свойств двух подсистем по показателю С_п [3] (см. табл. 1).

Значение показателя	Влияние подсистемы
СП » 1	Подсистема оказывает небольшое влияние на динамику системы. Динамическая декомпозиция возможна.
СП « 1	Подсистема оказывает небольшое влияние на динамику системы. Динамическая декомпозиция возможна.
СП≈ 1	Обе подсистемы оказывают примерно одинаковое влияние на динамику системы. Динамическая декомпозиция этих систем не возможна.

При определении индексов суммирования р_i и р_j следует исходить из того, что динамическое поведение элемента ТГУ характеризуется не более чем четырьмя величинами: постоянными времени первого и второго порядка; временем запаздывания и постоянной времени предварения. Если известны значения этих величин, то показатель С_П позволяет решить вопрос о возможности динамической декомпозиции. Приведенное выше сопоставление позволяет оценить влияние динамических свойств отдельных подсистем по показателю С_П . Практически можно считать, что для динамической декомпозиции двух подсистем достаточно, чтобы выполнялось условие: С_П >20 или С_П < 0,05.

Хотя показатель С_П и позволяет сравнить динамическое поведение подсистем, тем не менее, он не дает информации о соотношении между динамическими свойствами рассматриваемой подсистемы и динамическими свойствами вектора входной величины U(t) этой подсистемы. Очевидно, что значительные изменения выходной величины >>(/) при имеющихся изменениях U(t) возникают только в том случае, если собственная частота j - й подсистемы находится в определенном от ношении к верхней предельной частоте ω_к входной величины. Если принять отношение:

как показатель, то ситуации, возникающие при оценке фильтрующих свойств подсистемы ТГУ с помощью показателя С_П1 будут соответствовать табл. 2.

Таблица 2

Значение показателя	Влияние подсистемы
CП1 » 1	Сильное фильтрующее действие подсистемы
CП1 « 1	Отсутствие фильтрующего действия подсистемы
CП1 ≈ 1	Переходная область: заметное фильтрующее действие подсистемы

Для инженерных расчетов можно положить, что для динамики важна область отношения частот от двух до трех декад. Поэтому выполнение неравенства С_т >20...30 можно считать достаточным условием для квазистационарного моделирования, j -й подсистемы по отношению к входной величине.

Предложенные показатели были использованы для упрощения математической модели динамических характеристик (структурной схемы) системы регулирования температуры теплоносителя ТГУ (рис. 1).

5

4444

3

2

1

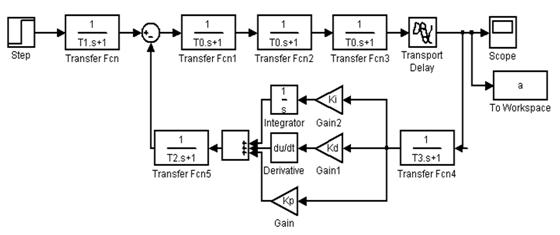
Рис. 1. Структурная схема системы регулирования температуры

(1 - входное воздействие; 2 - объект регулирования; 3 - датчик температуры; 4 - регулятор; 5 - исполнительный механизм и регулирующий орган)

Выполнялась динамическая декомпозиция с использованием параметра С_П и исследование влияния ряда звеньев на ошибку аппроксимации (рис. 2).

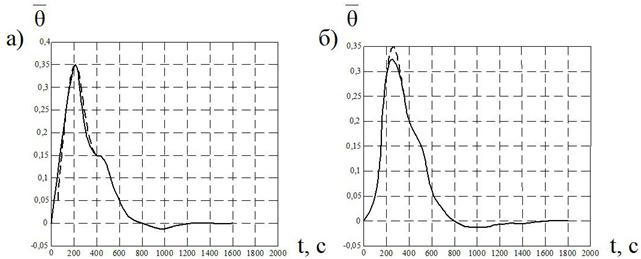
Рис. 2. Результаты динамической декомпозиции (а - влияние звена 3, С_П = 0,04; б - влияние звена 5, С_П - 0,03)

Проведенные исследования показали, что при анализе динамики, определении оптимальных настроек регулятора системы [1, 2] структурная схема может быть упрощена без внесения существенной погрешности в конечный результат. Влиянием звеньев 3 и 5 (рис. 1) при этом можно пренебречь.

Кроме того, более детальное исследование позволило сделать некоторые общие выводы: влияние цепочки последовательно соединенных звеньев (рис. 1) можно оценить суммированием постоянных времени этих звеньев; возмущения в системах с обратной связью затухают значительно медленнее, чем в разомкнутых системах; для систем, содержащих нелинейные звенья также целесообразно применять принцип динамической декомпозиции, при этом нелинейную часть системы необходимо разделить на нелинейные статические и динамические звенья, а затем применить принцип декомпозиции для линейной части.

Литература:

1. Коваленко, А.А. Взаимовлияние процессов тепломассопереноса в котельных установках/А.А. Коваленко, Я.А. Гусенцова, Н.Д. Андрийчук. - Луганск: изд-во ЛНУ им. В.Даля, 2017.- 196 с.

2. Розенвассер, Е.Н. Чувствительность систем автоматического управления / Е.Н. Розенвассер, P.M. Юсупов. - М.: Наука, 1981. - 46 с.

3. Осенин, Ю.И. Декомпозиция процесса теплопередачи в системе охлаждения теплоносителя тепловоза/ Ю.И. Осени, Ю.В. Баранич. - Луганск: изд-во ВНУ им. В.Даля, 2006.- 124 с.

4. Цветков, Ф.Ф. Тепломассообмен: учебник для ВУЗов / Ф.Ф. Цветков. - М.: МЭИ, 2011. - 562 c.