Экономические
науки/Математические методы в экономике
Master student
Aristombaeva M.T.,
students Abilkhanova Zh.K.,
Auezova A.S., Kozhakova D.N., Sambetova M.E.
Research supervisor Candidate of Technical Sciences
Kurmanov B.K.
Kazakh-British Technical University, Kazakhstan
Assessment
of attractiveness of the investment project by the method imitating modelling
The
investment project is developed, based on certain assumptions on capital and
current expenses, sales volumes of manufactured products, prices of goods,
project time frame. Regardless of the quality and validity of these
assumptions, future development related to the implementation of the project is
not ambiguously. In this case, using of investment design consider uncertainty
and risk aspects.
In analyzing of investment projects modern economists faced with need to
consider risk so cash flows of any project can be represented in the
probability-theoretic sense of some-of random variables. In this case, all
parameters of economical mathematical cash flow models are divided into
Quasideterministic (parameters that are unchanged and exactly knownin the
development of this investment project) and random (impacted by several
factors: economic, political, social, etc.). Since all parameters of economical
mathematical models of cash flows interact with each other so statistical
characteristics of random cash flows can be found with using of simulation cash
flows [1].
If we
assume that the annual output (Q), the expected cost (p), variable cost per
unit of output (v) and annual fixed costs (F) is the value of
Quasideterministic, the cash flow for a given tax rate (t) can be determined by
the formula:
С = ![]()
![]()
![]() otherwise
otherwise
In
general, these variables in the formula are random variables with given
distribution laws and procedure of finding random cash flows to conduct a
series of algebraic operations on random variables and in the result to get
distribution law of the random cash flows. Such task is quite time-consuming
and not always feasible, because addition or multiplication operations of
random variables described by distribution law are quite complex.
Simulation modeling is one of the most powerful methods for the analysis
of economic systems. In general, imitating is the process
of conducting experiments on the computer with mathematical models of complex
real-world systems. The objectives of these experiments
can be different from identifying properties and laws of the system to solving
specific problems. With the development of computer software and hardware the using of simulation modeling has grown considerably in economic
sphere. Currently, it is used to solve problems
in internal control of companies and modeling management
on macroeconomic level.
Imitating modeling is based on the use of random number generators. Random
number generator is a computer program that generates sequence of random
numbers in accordance with a certain distribution. In
general, conducting of imitating experiments in
the implementing of following steps:
·
establish the relation between
input and output indicators in the form of the mathematical equation or in
equality;
·
set the laws of probability distribution of key parameters of the model;
·
carry out a computer
simulations of the key parameters of the model;
·
calculate the main
characteristics of the distributions of input and output indicators;
·
analyze the results and make a decision.
Actuality of the question is the using of
imitating modeling technology to allow to do analysis of all factors and circumstances that may lead to a decrease in
expected future income, compared with the predicted [2].
For the simulation of random cash flows we used modern object-oriented system GPSS World (General purpose simulation system), which is a universal
language of imitating modeling [3,4].
We assume that the price of the product, production
volume and variable costs per unit are random numbers, which distributed by the
normal distribution law with given mean value and
deviation from the average. Modeling algorithm of cash
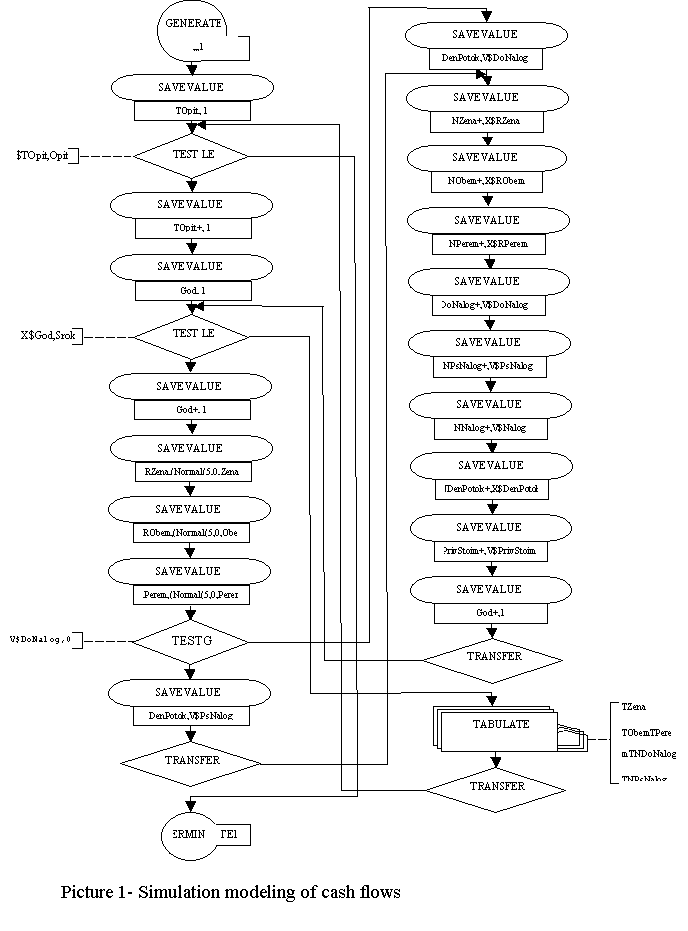
flows with the using of blocks GPSS World is shown in Figure1. In the figure were used the following
notations: Srok–period of
the project (n); Zena - average price for unit of the product(p); Obem - average annual production
volume (Q); Perem - average
variable cost for unit of the product (v); Post - fixed cost for the year (F); Invest - initial
investment (I0),
Stavka - tax rate (t);
Diskont- discount rate (d); Opit - number of ongoing imitating experiments.
In the
modeling also were used the number of variables, description and formulas for
calculation that are given in table 1.
Table 1
– Calculated variables used in imitation modeling
|
Description |
Notation |
Formula |
|
Income for year without
paying tax |
DoNalog |
X$RObem*(X$RZena-X$RPerem)-Post |
|
Income for year with paying
tax |
PsNalog |
V$DoNalog-V$Nalog |
|
Average value of given price
in project period |
VZena |
X$NZena/Srok |
|
Present value |
PrivStoim |
X$DenPotok/(1+Diskont)^X$God |
|
The sum of paid
tax for year |
Nalog |
V$ObNalog*Stavka |
This algorithm is explained as
following:
Block GENERATE
forms a single transact (dynamic object), which in this case will constitute a calculator (occurrence of a
dynamic object to GPSS block initiates the activation of the block).
 0251661312251662336251663360251664384251665408251666432251667456251668480251669504251670528251671552251672576251673600
0251661312251662336251663360251664384251665408251666432251667456251668480251669504251670528251671552251672576251673600
When
the transact entered to the block SAVEVALUE (save value) put a value of 1 in
the stored value TOpit, indicating thereby
that the first imitating experiment is begin. Testing block TEST (test)
checks the correctness of execution
number of experiments (LE means ≤). If the execution is correct, the
imitation will continue. In other case the transact goes to TERMINATE block and
imitating modeling will be finished.
Next
two SAVEVALUE blocks are the counter of experiments and sets the initial value
of counter of number of the project`s past years to 1, which initiatethe
beginning of the first year of project.
Following
TEST LE block controls the end of the project period. If the period is not
done, costs, variable expenses and the amount of products will be played by
normal distribution law (next three blocks of SAVEVALUE). When the project
period is finished, the group of blocks TABULATE (record in the table) will put
statistic data into corresponding table and block TRANSFER (transfer) moves it
to next experiment.
Block
TEST G (>) checks whether to pay tax on profit or not (the profit is
available). If yes, that is defined a cash flow after payment tax and further
the group of SAVEVALUE blocks accumulating data on receipts, the paid tax and
on the specified cost from year to year for project life term follows. Then
carried transition to the next year's project (via the TRANSFER block).
To
illustrate of the given imitatingmodelling we consider specific example.
Let
project period is n=5. Cost of the production, annual output and annual
variable expenses are distributed in normal distribution law with mean value
p=320, Q=15000, v=230, the average deviations make 10% of percent of average
random values. Also it is considered that annual constant expenses F=700000,
volume of investment I0=600000, a tax rate of t = 30% and norm of discount
d=15%. The number of imitating experiments equal 1000, it is enough toreceive
certain results.
In the
process of modelling we will take that average value of the price for the
project period is 320,03 monetary units, production volume – 74951 units of
products, variable expenses – 1149,5 monetary units, the cash flow after
payment of a tax makes 2277601.03 monetary units, the volume of the paid tax –
976114.728 monetary units. The specified cost makes 1479953 that for our
example almost exceeds investment volume twice.
We will
note that results of the modeling can differ from calculation results in
assuming of deterministic values to several percent depending on degree of
dispersion of random variables from the average. In our example (the dispersion
from the average is10%) the calculated value of a cash flow after payment of
the tax is 2275000 that differs from results of modeling approximately for
0,1%.
In
conclusion, using of imitating modeling devicesallows to consider uncertainty
factors, on the basisof using of random
variables in modellingthat gives opportunity to present an economic situation
as it is possible closer to reality that increases objectivity of an
assessment. Such approach considerably increases probability of making correct
decisions in the choice of investment projects.
References:
1.
Yurshevich E.A. Imitating modeling of risks in
business processes. Transport and communication. Volume 3, No. 4, M., 2002
2.
Leifer L.A, Vozhik S.V., Dubovkin A.V. Using of
imitating modeling for forecasting of cash flows of the enterprise and risk
analysis in the business assessment. The property relations in the Russian
Federation, No. 4, M., 2003
3.
GPSS World Tutorial Manual. Copyright Minuteman
Software. Holly Springs, NC, U.S.A. 2001.
4.
Kurmanov B. K., Kurmanov G. B. Development of
imitating models on GPSS World. Manual. – Almaty: Publishing center JSC KBTU,
2011.