ЖЕТИМЕКОВА ГАУХАР ЖЕНИСОВНА

КАЗАХСТАН, Г.КАРАГАНДА

АЛГОРИТМ РАСПОЗНАВАНИЯ ДЛЯ ЗАДАЧ С  ПЕРЕСЕКАЮЩИМИСЯ КЛАССАМИ НА ОСНОВЕ НЕЧЕТКОЙ МОДЕЛИ НЕЙРОСЕТИ

 

The objective of this approach is to combine the particularities of fuzzy theory (using fuzzy membership  p functions) and the particularities of neural network (with a learning process ability by using backpropagation algorithm and a high-speed parallel structures) to construct a special neural fuzzy network which can learn from environments. It has been applied this approach on the nonlinear intersection Iris dataset that consists of three classes and the breast cancer dataset that consists of two classes of benign and malignant.

 

Искусственные нейронные сети  (ИНС) – это математические модели, разрабатываемые для сохранения и обработки некоторой информации, отражающие возможности мозга высокоразвитых животных и мозга человека. Данные модели разрабатываются согласно работе биологического нейрона, подобно ячейкам, соединенным посредством связей с корректируемыми силами/весами.

Способы распознавания образов могут быть с обучением и без обучения.  Сеть с обучением учится с помощью примеров обучения. Сеть без обучения учится, обнаруживая подобие во входных образцах. Алгоритм обучения  обратным распространением - алгоритм с обучением. Сеть без обучения более приемлема для самоорганизованных сетей. [1]

            Модель нейронной сети с обратным распространением ошибки (ОРО) является наиболее популярной моделью в нейронных сетях. Она не имеет соединений обратной связи, но в процессе обучения появляются ошибки обратного распространения.  Цель - получить наименьшую ошибку. Многие приложения могут быть сформулированы с использованием алгоритма обратного распространения, и эта методология была применена для большинства многослойных нейронных сетей.

            Правило обучения распростронение ошибки (ОРО) для многослойной нейронной сети – это обобщение правила дельта-обучение. Модели искусственного нейрона используются для задач распознавания образов с 1950 г. Исходная версия алгоритма ОРО, неудобна для пользователей по многим причинам. [2]

1. Если алгоритм действительно имеет сходимость, то сходится чрезвычайно медленно.

2. Процесс может застрять в локальных минимумах .

3.Чувствительность к состоянию весов, функции энергии, и мощности обучающегося множества.            Существует несколько методов для улучшения алгоритма ОРО. Существует множество проблемных областей (задач), в которых некоторые точки (элементы) полностью принадлежат одному классу, но могут также частично принадлежать другому классу. Когда классы пересекаются, то есть, когда часть    данных принадлежат больше чем одному классу, тогда бинарные значения выходов,  теряют  однозначную  классификацию для этих классов.

  Так что нечеткость данных всех классов лучше, чем их  однозначная принадлежность бинарным значениям. Другой путь состоит в том, чтобы расширить веса и/или вводы и/или выходы (или цели), используя нечеткие числа. Buckley и Hayashi вывели три возможности:

1. четкие входные данные, нечеткие веса, нечеткие выходные данные

2. нечеткие входные данные, четкие веса, нечеткие выходные данные

3. нечеткие входные данные, нечеткие веса, нечеткие выходные данные.

            Был использован первый тип нечеткого нейрона. Этот подход предполагает нечеткость входных векторов через некоторые особенности статистических наборов данных для вычисления функции членства (принадлежности) каждого класса. [3] Для  решения  задачи  распознавания   предлагается использовать p-функцию для фазиффикации  модели.

            Процесс обучения должен быть запущен соответственно первоначальным весам для обучения сети. Возможно использовать генетические алгоритмы для установления начальных весов и начала процесса обучения сети. Однако, установление несоответствующих начальных весов – одна из причин чтобы попасть в локальный минимум (неглубокую долину), в то время как рядом есть более глубокий минимум или войти в неопределенно долгий процесс обучения. Поэтому здесь начальные веса были сгенерированы случайными значениями. [4]

            Алгоритм обратного распространения – один из базовых алгоритмов, применяемых для изучения нейронных сетей. Он был изобретен несколько раз разными исследователями, Bryson и Ho, Werbos, Parker и Rumelhart, Hinton, и Williams. Алгоритм состоит в такой подстройке весов, чтобы заданному входному вектору сеть ставила в соответствие целевой выходной вектор.

Обратное распространение не всегда сходилось в дискретных моделированиях. Некоторые значения начальных условий вели к колебаниям, даже к хаотическому блужданию.

Некоторые защитники обратного распространения утверждали, что алгоритм должен сходиться в случае применения метода градиентного спуска на поверхности ошибки в синоптическом “пространстве весов”. [5] Шар пространства состояний просто должен был прокрутить вниз поверхность ошибки к самому близкому минимуму ошибки и остановке.

Ошибки на выходах накапливаются в результате ошибок в скрытых слоях, и используются как основание для регулирования весов между входными и скрытыми слоями. Корректировка двух наборов весов между парами слоев и перевычисление выходов - итерационный процесс, который продолжается до падения ошибок ниже уровня допустимого. Изучение нормы параметров масштабирует корректировки весов. Параметр импульса может также использоваться в масштабировании корректировок от предыдущей итерации и добавления к корректировкам в текущей итерации.

Базовый Алгоритм Обратного распространения Ошибки

Искусственные нейронные сети состоит из нескольких слоев - входной слой, скрытые слои и выходной слой. Один скрытый слой показан на рис.1. Связи между каждыми двумя слоями называют весами, которые инициализированы  в  начальный момент  маленькими случайными числами между 1 и – 1 при  запуске процесса обучения сети. С примечаниями сети, вход в сеть к нейрону i в слое l+1.  Образец входа xp = {xp1, xp2, …, xpn} значение нейрона в слое l+1 вычислено Уравнением (1).

 

 

 

 

 

 

Рис. 1  Три слои нейросети структура

            (1)

где  представляет вес между нейроном j в слое l и нейроне i в нижнем слое l-1,  - выход нейрона j в слое l, такой, что, в первом слое является равным , чтобы ввести образец xp.

            Сигмоидальные функции на рисунке (2.a, 2.b) обычно используются как функция активации. Здесь две сигмоидальных функции: гиперболическая функция тангенса со значениями в (-1,1), и логистическая функция, имещая значения между (0, 1). Будем использовать логистическую функцию, выход нейрона l с сетевым входом    

        (2)

где, b определяет крутизну функции активации. Обычно b  принимает значение  1.

                              

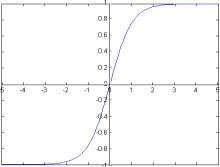
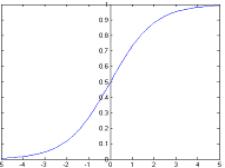
Рис 2.a  Сигмоид  f(x)= tanh (x)                               Рис.2.b  Сигмоид  f(x)=1/(1+e -x)

 

Дельта- Правило

Алгоритм ОРО представляет входной образец, чтобы ввести слой NN, который бы воздействовал на сеть, производя выход. Этот выход иной, по сравнению с желаемым или целевым выходом. Различие между фактическим выходом и желаемым выходом называют дельтой или ошибкой. Ошибка  epi  для  i-го нейрона выходного слоя o для входной обучающей пары (xp , dp) вычисляется как

     (3)

Цель алгоритма состоит в том, чтобы использовать эту ошибку для корректирования весов в пути, для постепенного уменьшения ошибки. Таким образом, алгоритм обучения изменяет веса, используя некоторую процедуру, которая не гарантирует никакого увеличения в значении объективной функции. Объективные функции известны как функции энергии.

            Rumelhart и другие в их оригинале ОРО использовали сумму квадратов ошибки как функцию энергии E. Существует две версии алгоритма ОРО, интерактивный (online) and пакетный (batch).  [6] В интерактивном ОРО веса обновляются  согласно ошибке при  передаче каждой обучающей паре , этот метод использует  функцию энергии, определенную в уравнении (5). В пакетном алгоритме  веса обновляются после накопления ошибок во всех обучающих парах и этот метод использует функцию энергии, определенную в уравнении (4).

           (4)

             (5)

где  no – число выходов,  P число обучающих пар

Метод градиентного спуска  

Сеть обратного распространения по существу использует разновидность метода градиентного спуска, т.к. осуществляет спуск по поверхности ошибки, непрерывно подстраивая веса в направлении - к минимуму. Мы можем изменить к лучшему набор весов, двигая скоростной спуск по поверхности в w пространстве.

Определенно, обычный алгоритм градиентного спуска   предлагает изменение каждого  количеством , пропорциональным градиенту квадратной ошибки E:

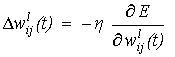              (6)

где, h - размер шага или изучение коэффициента скорости, t - итерация или номер шага в процессе обучения. Правая часть уравнения пропорциональна частичной производной E относительно веса. Вместо Уравнения (7) часто используется, чтобы приспособить размер как функция местного искривления поверхности ошибки. Уравнение (6) изменяет в векторах веса только в направлениях входных векторов образца. Таким образом, любой компонент весов, ортогональных к образцам оставляет неизменным спуск. В пределах подпространства образца метод градиентного спуска обязательно уменьшает ошибку, если h является достаточно маленьким. Таким образом, через некоторое множество итераций, мы приближаемся к основанию точки минимума близко от любой отправной точки как показано в рис. (3). Функцией модифицирования веса для пакетного режима дают

 

Рис. (3).
 
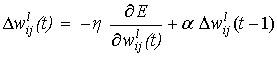                                (7)                                                                                                               

                                               (8)                                                                                                            

 

где, α - коэффициент момента, который может иметь значение между 0 и 1. Второе слагаемое  делает текущее направление поиска показательным взвешенным средним числом последних направлений. Для интерактивного ОРО, модифицирующего вес правила, функция энергии в Уравнении (7) - замененная энергия Ep.

     (9)     

 

Что касается выражения для   от Уравнения 1, просто найти это

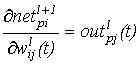        (10)

Выражения для   различные для скрытого слоя нейронов и выходного слоя нейронов. Таким образом это удобный обозначить  = - . Правило обновления весов в уравнении есть

   (11)

Используя сигмоидальную функцию (Уравнение (2))

с β =1, для выходного слоя

      (12)     

и, для скрытого слоя, сигнал ошибки ЕС ь

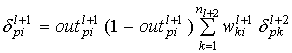   (13)

Из уравнения (12) ясно, что сигнал ошибки вычислен непосредственно из соответствующей ошибки, но сигнал ошибки для нейронов в скрытых уровнях получен размножением сигналов ошибки нейронов в слое только после этого, как это: алгоритм Обратного Распространения ошибки. Рисунок 4 иллюстрирует вычисление сигналов ошибки для нейрона i в слое l+1.                                               

 

                                                     

                                                                                                         

·

·

·
 
                                                                                                                                                                   

                                                                                                                            

                                                                                                         

                                                                                                                   

 

 

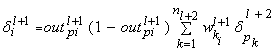
Рис. 4. Вычисление сигнала ошибки

Объединяя уравнение (11) с уравнением (12), можно вычислить исправления веса для нейронов выходного слоя. Точно так же исправление веса для скрытых нейронов уровня может быть вычислено, объединяя Уравнение (11) с Уравнением (13). Процесс обучения упреждения искусственной нейронной сети  - итерационный процесс.

Каждая итерация процесса обучения нейронной сети состоит из следующих шагов:

1) Выбор входной обучающей пары (xp , dp) .

2) Проход Вперед:

 представьте входной образец xp и определите его выход. Уравнения (1) и (2) необходимы для вычисления этого прохода.

3) Проход  в обратном направлении:

Вычислите сигнал ошибки для каждого нейрона. Должно быть отмечено, что ошибка сообщает о запусках вычисления от выходного слоя и до  входов в обратном направлении к скрытым слоям. Например, если ИНС имеет четыре уровня - один входной слой, два скрытых слоя, и один выходной слой - тогда сначала вычисляются сигналы ошибки для нейронов выходного слоя. Вычисляются сигналы ошибки для второго скрытого слоя нейронов. Вычисляются Сигналы ошибки для первого скрытого слоя нейронов (наиболее близких к входному слою).

4) Корректировки Веса: Корректируйте веса, используя Уравнение (11) согласно версии типа изучения Пакетной или Интерактивной Версии.

            Каждый образец представлен однажды, и исправление веса рассчитано, но веса фактически не откорректированы; и расчетные исправления веса для каждого веса добавляются вместе для всех образцов, и затем веса откорректированы только однажды использование совокупного исправления.  

Интерактивная Версия:

Значения нескольких параметров важны в осуществлении ОРО алгоритма. Начальное значение весов должно быть маленьким и выбрано случайным образом, чтобы избежать проблемы симметрии. Sietsma и Dow  использовали однородно распределенные случайные числа между-0.5 и 0.5 как веса смещения, и между (-0.5/nl) и (0.5/сш) как начальные веса для связей между слоями l и l+1. Обратите внимание, что деление на nl дает число входов нейрона.

Значение h играет очень важную роль. Меньшее значение h делает обучение медленным, но слишком большое значение h вызывает колебание, препятствующие сети обучить задачу. Практически, самое эффективное значение h зависит от проблемы. Например, Fahlam взял коэффициент 0.9 для изучения одной проблемы, а Hinton  взял 0.002 как коэффициент скорости обучения для другой проблемы. Изменение в значении обучения оценивает коэффициент h для более быстрого обучения.

Для решения задач распознавания с пересекающимся классами за счет использования  для фаззификации p-функции принадлежности построена модель нечеткой нейросети.

Для этой  нейросети в алгоритме обучения удалось использовать алгоритм обратного распространения  и  для того чтобы ускорить процедуру обучения сети используется, учитывая особенности градиентного пространства динамически изменяемый коэффициент обучения. 

 

Литература

1. Головко В.А. Нейроинтеллект: Теория и применения. Книга 1. Организация и обучение нейронных сетей с прямыми и обратными связями - Брест:БПИ, 1999, - 260с.

2. Головко В.А. Нейроинтеллект: Теория и применения. Книга 2. Самоорганизация, отказоустойчивость и применение нейронных сетей - Брест:БПИ, 1999, - 228с.

3. Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика, 1992 - 184 с.

4. A.I. Wasserman, “Neural Computing: Theory and Practice,” Van Nostrand Reinhold, New York, 1989.

5. Ежов А.А., Шумский С.А. – Нейрокомпьютинг и его применения в экономике и бизнесе. – Москва, 1998.

6. Вороновский Г.К., Махотило К.В., Петрашев С.Н., Сергеев С.А. – Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности. – Харьков:Основа, 1997.