ПОСЛЕДОВАТЕЛЬНАЯ РЕГРЕССИОННАЯ ИДЕНТИФИКАЦИЯ

ДИНАМИЧЕСКИХ СИСТЕМ

Петренко В.О., Гарькина И.А.

Пензенский государственный университет архитектуры и строительства

Для иллюстрации рассмотрим класс эргатических систем [1], описываемых уравнениями движения:

;

- управляющие движения оператора.

В конечных разностях имеем:

,

или:

.

где - число измерений .

Параметры, доставляющие минимум функционалам качества ,

определятся из систем уравнений в матричной форме соответственно:

,	(1)
,	(2)

, , .

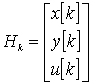
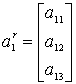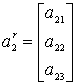Введем

,

(3)

Тогда из (1) следует:

, ;

(4)

а из (4) и (1):

, .

Справедливо:

.

Последняя формула легко приводится к виду

.

Получим рекуррентную формулу для оценки при r-ом измерении через оценку при (r-1)-ом измерении . Аналогично - для оценки : . Оценку можно получить рекуррентно по предыдущей оценке и по измерениям ,, если матрица так же получена последовательно.

По (3):

.

(5)

Если известно начальное значение матрицы , то, умножая (5) слева на , получим:

;

(6)

а умножив на (6) справа, -

.

(7)

Из (7), умножая на справа, получим:

.

Умножая далее справа на , получим:

.

(8)

Подставив в (7) из (8), имеем

.

Получили окончательный вид рекуррентной формулы:

.

(здесь ; начальная оценка может быть произвольной).

В развернутом виде формула (8) имеет вид:

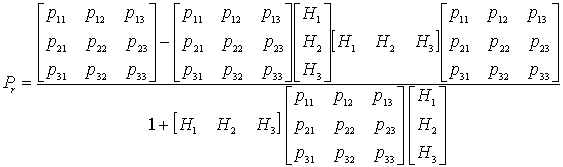
Алгоритм идентификации непосредственно вытекает из:

; ,

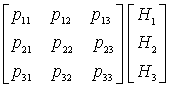
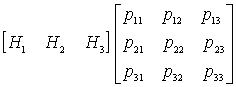
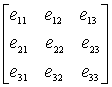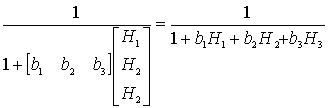
; q.

Для рассматриваемого класса систем можно принять:

, ; .
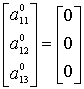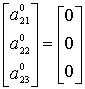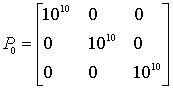