ПРИЛОЖЕНИЯ МЕТОДОВ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА

К СИНТЕЗУ СЛОЖНЫХ СИСТЕМ

Карев М.Н., Данилов А.М.

Пензенский государственный университет архитектуры и строительства

Проиллюстрируем использование методов планирования эксперимента на двух конкретных реализованных проектах систем.

1. Рассмотрим некоторый объект с оптимально настроенным автоматом стабилизации:

;

,

где - обобщенные координаты; - команда управления, .

Целью эксперимента является определение значений параметров управляющего сигнала и , при которых целевая функция достигает своего минимума при апериодичности переходного процесса . Здесь - время перехода (в режиме управления) объекта с одного значения на другое. Примем

.

Определенная по данным таблицы ПФЭ 2² (табл.1,2) зависимость имеет вид

.

Далее производилось крутое восхождение; результаты приводятся в таблице 3.

Таблица 1

1	-	-	14,6
2	+	-	14,0
3	-	+	14,8

Таблица 2

Исходные данные	, м	, град
Основной уровень	31,5	30
	0,8	0,6
	-0,35	0,05
	-0,28	-
	1	-

Таблица 3

1	31,5	30	14,6
2	32	30	14,2
3	32,5	30	14,0
4	33	30	13,7
5	33,5	30	13,5

Можно убедиться, что точка =33,5; =30 является почти стационарной; . Исследование окрестности этой точки с применением ортого-

нального центрально-композиционного плана дает

.

1. Рассмотрим более сложную задачу, связанную с синтезом маломощной электромеханической слабодемпфированной управляемой системы, уравнения движения которой в векторной форме имеют вид

;	(1)
;	(2)

; - матрицы с размерностями соответственно;.

Систему (1)- (2) можно привести к виду

; ; ;

; .

Матрица и столбец имеют блочную структуру:

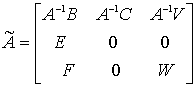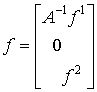
, , - единичная матрица.

Исходя из требований к системе управлений, целевая функция принималась в виде 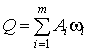, где и максимальные амплитуды и соответствующие им частоты, отобранные из условий в разложении в ряд Фурье ошибки системы; - коэффициенты Фурье.

Использовалась приводимая ниже методика синтеза, включающая итерационную процедуру.

1. В первом приближении a'priori задавались структурная схема системы автоматического управления (САУ) и конструктивные подсистемы и параметры упругодемпфирующих связей между ними (конструктивная схема).

2. В соответствии с п.1 составляются уравнения движения (математическая модель).

3. По предварительным конструктивным и динамическим проработкам устанавливалась область изменения параметров .

4. По результатам линейного синтеза выбиралась исходная точка в пространстве параметров.

5. Методом Бокса-Уилсона определялись и точка , в которой ;.

6. Если требуемая точность САУ не достигалась, то задавалась ее уточненная структурная схема при прежней конструктивной схеме и далее выполнялись пп.2-5.

7. Если требуемая точность САУ вновь не достигалась, производилась коррекция конструктивной схемы и выполнялись пп.2-6 и т.д.

В каждом необходимом случае определялась в результате интегрирования уравнений движения с параллельным разложением в ряд Фурье ошибки САУ в диапазоне ; промежуток времени , как и весь диапазон рассматриваемых частот, определялся из конструктивных соображений (для изучаемых систем 20с, ). Сначала в пространстве параметров решалась задача , где реальные части корней характеристического уравнения. Взяв полученную в результате решения этой задачи точку в пространстве параметров в качестве исходной, методом Бокса-Уилсона производилась оптимизация параметров линейной системы по критерию , - соответственно отобранные резонансные частоты колебаний системы и соответствующие им частоты. Точка, оптимальная в смысле минимума , принималась за исходную точку для нелинейного синтеза, который производился по изложенной выше методике. Выбор целевой функции осуществлялся, исходя из приоритета требований к скоростям перед фазовыми координатами; жесткости конструктивных элементов относительно их прочности.