Д.т.н. Заднепровский Р.П.

Волгоградский государственный архитектурно-строительный университет, Россия

О впитывании суспензированных жидкостей в дисперсные пористые породы

Даны уравнения впитывания суспензированных жидкостей с нератворимыми взвесями и их анализ применительно к пористым грунтам при постоянной и переменной интенсивности подачи жидкостей.

Ключевые слова: уравнения впитывания, просачивание жидкостей с нерастворимыми примесями, инфильтрация, движущие потенциалы просачивания жидкостей в пористые среды

Известны эмпирические и теоретические зависимости для расчета скорости впитывания в стадии просачивания жидкой фазы в пористые тела типа почвогрунтов [ 1,2 ]. В этих уравнениях наличие взвесей в жидкости или характер изменения ее свойств, как правило, не учитывается. Наиболее исследована фаза фильтрации применительно к технологическому процессу очистки природных и сточных вод. Такая очистка с использованием песка различной дисперсности исследована в работе Ю. А. Ищенко [ 6 ], где приведены эмпирические формулы для скорости фильтрования.

Ряд исследований по фазам просачивания и инфильтрации влаги основывается на явлениях диффузии и различных характеристик влажности среды (относительная влажность, максимальная и молекулярная влагоемкость и им подобные характеристики ). Например, в работе [ 4 ] приводится уравнение диффузии ( по Гарднеру), где коэффициент диффузии ( как функция влажности) D = D, где - соответственно, сложные нелинейные эмпирические или полуэмпирические функции характеристик влагоемкостей различного уровня. При этом, наличие дробных степеней этих функций и отсутствие явной связи с осоновными измеряемыми физическими параметрами пористых тел и явлениями сопровождающими капиллярный перенос сильно затрудняют корректный анализ влияния физических показателей на анализ процесса впитывания для различных конкретных случаев суммарного движущего потенциала течения жидкостей в пористой среде. Наличие опытных коэффициентов, не связанных с конкретными свойствами почво-грунтов, не позволяет, хотя бы приближенно, оценить влияние этих свойств на характер впитывания. Теоретические зависимости перемещения влаги в почве, полученные на основе теории тепломассопроводности, весьма сложны и также не решают эту задачу.

Вывод и решение основных уравнений впитывания ( для постоянной и переменной массы жидкости без учета взвесей) [1] основан на дифференциальной форме закона Ньютона с учетом конкретных свойств почвогрунтов. При этом, передвижение влаги под действием градиентов температуры, неравновесной пленочной влажности и концентрации солей не учитывалось, ввиду малой скорости этих процессов по сравнению со скоростью инфильтрации (особенно в первые 2 часа), а глубина промачивания практически имела конечное значение. Ниже дается вывод комплекса уравнений инфильтрации, включая все три стадии: смачивание, просачивание, фильтрация с вариациями общего движущего потенциала, учитывающего изменение физико-механических свойств системы пористая среда – загрязненная жидкость (влага). В случае одномерной задачи (движение влаги вглубь пористой среды перпендикулярно внешней плоскости)

d(mV)/dt = + mg ( 1 )

При значительном размере плоского участка выражение ( 1 ) пригодно и для оценки двухмерного движения. Двух-трехмерную модель имеет смысл рассматривать лишь для краев участка, ограниченного зоной действия гидроисточника.

Сумма сил – Р ( или их потенциалов) слагается из сил тяжести mg, трения - Р_т, капиллярного давления Р, сопротивления защемленного воздуха Р_е и гидравлических сопротивлений Р_г (слияния, повороты). В общем случае, активный (движущий) потенциал р=р+ р, где к частным потенциала сил могут относится, соответственно: напор из локального источника поступления жидкости- р, капиллярный и температурный потенциал и, в ряде случаев –потенциал испарения Электродный потенциал -р и остальные движущие потенциалы рассмотренные в работе [ 5 ] несущественны и рассматриваются в особых случаях. В зависимости от структуры слоев и распределения температуры, капиллярный и температурные потенциалы могут менять направление (и соответствующий знак в их сумме). Молекулярно- адсорбционную часть поглощенной жидкости может быть учтена совокупной капиллярной силой. Для более детального анализа начальной скорости впитывания необходима отдельная оценка молекулярно-адсорбционного взаимодействия жидкости с поверхностями твердой фазы. Отметим, что так называемая «связанная влага» для суглинистых грунтов составляет 10-15%. Для упрощения решения в левую часть уравнения (1) вводим условное сопротивление боковой утечки Р. Физический смысл этой силы заключается в следующем. При передвижении воды вглубь почвы часть ее задерживается боковыми (горизонтальными) порами. Интенсивность этой боковой утечки определяется размерами пор, количеством, размерами и химико-физической активностью взвешенных частиц, временем соприкосновения с ними и достигнутой влажностью. То-есть, при движении массы воды т часть ее как бы теряется и движущаяся масса становится все меньше. Это эквивалентно некоторому условному сопротивлению. Считая движение в порах ламинарным, силы трения и гидравлических сопротивлений можно представить в виде , где коэффициент учитывает вязкость воды, пористость и текстуру (сложение) почвогрунтов.

Силы Р и Р_у являются в общем случае нелинейными функциями х (глубины впитывания), но при небольшой величине защемления воздуха и существенной глубине промачивания приближенно можно считать, что сумма Р. Cуммарный потенциал указанных выше сил сопротивления и движущих сил ( например, температурный потенциал) может менять знак и являться в конкретных ситуациях как силой сопротивления так и движущей силой, включающей и другие виды потенциалов , о которых говорилось выше. В общем случае при m = уравнение нелинейно. При наличии локально-точечного источника с перепадом подземного напора ориентировочная интенсивность подачи жидкости . В простейшем случае при m = const (впитывание слоя воды начальной высоты h₀) или, например, для дождя постоянной интенсивности масса, приходящаяся на единичную вертикальную пору m = at = rt. Здесь y- удельный вес, r - эквивалентный радиус, о - отношение площади участка к площади вертикальных пор (коэффициент живого сечения). После преобразований при m = const получаем

х - х - хb/m + P. + g = 0. ( 2 )

При равномерной подаче (m = at) или нелинейном расходе , учитывая основные варианты получаем следующие соотношения при переменной массе ( при просачивании по направлению сил тяжести - x):

tx** - Аx* - Dx + gt +Р/а = 0, ( 3 )

При неравномерной интенсивности подач ( притока) жидкости

(4 )

Здесь A = , D = , в большинстве случаев величина 0 < n < 3.

Для локального ( близкого к точечному ) источнику подачи жидкости с растеканием по сфероидным горизонтальным поверхностям при координате y R получаем:

ty**- Ay* - Dy + P = 0, (5 )

где D. Для сфероидных поверхностей с приведенным радиусом , изменяющимся от r до R коэффициент боковой утечки b. При растекании по горизонтальной плоскости ( координата –y) гравитационная сила отсутствует, а при движении вверх ( относительно координаты –x ) ее знак меняется.

Решение уравнения (3 ) находим в виде многочлена, считая

x = d₀ +t +- ... + d_xt^l.

Коэффициенты этого многочлена находятся по формуле Маклорена из краевых условий: при t = 0, х=0.

Общее решение уравнения ( 4 ) имеет вид

x* = V = V + (6)

Для значительных величин коэффициента А и достаточно большого числа слагаемых уравнения, уравнение принимает вид:

V где = V,

В окончательной форме получаем:

V = ( 7 )

Конечная скорость V, начальная скорость VP/38, коэффициент экспоненты .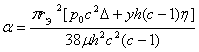

Капиллярное давление р= 2/r, где - поверхностное натяжение жидкости и угол смачивания частиц пористой среды. Капиллярная сила в расчете на одну пору Р, где к – коэффициент учитывающий форму пор . Для приближенных расчетов величина к = 2- 5 .

В общем случае при m = уравнение нелинейно. В простейшем случае m = const (впитывание слоя воды начальной высоты h₀) или, например, для дождя постоянной интенсивности р масса, приходящаяся на единичную вертикальную пору:

m = at = r. Здесь у — удельный вес, r_э — эквивалентный радиус (приведенный к круглой поре), о — отношение площади участка к площади вертикальных пор (коэффициент живого сечения).

Решение уравнения ( 3 ) при постоянной массе -m ( например, при начальном уровне жидкости на поверхности пористой твердой фазы – h ) имеет вид

V = V ( 8 )

где V, , m = y

После заполнения пор ( окончание фазы впитывания) уравнение (3) примет вид

. Частное решение этого уравнения для фазы фильтрации:

V= P/ (9 )

Это уравнение по форме аналогично известному уравнению Дарси.

Для сплошного затопления слоем значительной высоты можно записать в общем виде :

V = V, ( 10 )

Структура основных уравнений ( 7-10 ) может быть использована и для загрязненных суспензированных жидкостей и их смесей после внесения поправок в коэффициенты а,b,,,отражающие характерные параметры загрязненных жидкостей. Для этих жидкостей возрастают значения приведенной вязкости - , эквивалентного размера частиц взвесей –r, снижаются глубина просачивания, коэффициент живого сечения пористой среды - и соответствующее время впитывания.

Рассмотрим эти поправки с учетом характеристик взвесей. Можно разделить взвеси на две основные группы: взвеси со слабосвязанными частицами и агреатирующиеся ( золи, коллоиды, клатраты и др.). В реальности могут быть промежуточные подклассы. Для учета изменения вязкости растворов с твердыми частицами , для разбавленных суспензий можно использовать формулу ,[ 3 ], а для устойчивых взвесей . Здесь - соответственно : вязкость дисперсионной среды, коэффициент формы частиц и обьемная концентрация взвеси.

Для несферических частиц коэффициент f > 2,5. Для суспензий с полимерными частицами концентрацией более1% резкое повышение вязкости связано с увеличением молекулярного взаимодейсвия . Отметим, что в природной воде могут быть частицы размером 1-100 мкм с обьемным содержанием до 1%. В первом приближении коэффициент учитывающий форму частиц А= S/, где S, - соответственно, площадь поверхности частицы и ее обьем. Для реальных размеров частиц сфероидной и плоской формы величина А = 2 – 10. Для природных суглинков А = 2-4. Для скоростных потоков ( при значительном отклонении от ламинарного просачивания) вычисляется динамический коэффициент формы Г= 1+0,35(А-1) [ 6 ]. Этот коэффициент применим для быстоосаждающихся взвесей при размере частиц более 1мкм. Для частиц с размером менее 10 наблюдается обратно пропорциональная зависимость времени осаждения от размера частиц.

Для определения скорости фильтрации через песчаные смеси [ 7 ] предложена опытная зависимость V = 1/ 4,6 – 6,4 [exp( - d)] , где d относительное соотношение условного и эквивалентного размера частиц фильтрующей среды. При этом следует отметить:

графики предельного насыщения частицами взвеси среды по ее глубине имеют вид близкий к экспоненте, а зависимость массы отложений взвесей в среде от скорости фильтрования имеет гиперболический характер ( при наличии критической скорости в интервале V = 2-10м/с в закольматированном песке при d = 0,2-0,6мм ).

Закупорка пор – основная причина резкого снижения скорости впитывания и прекращения процесса фильтрации жидкостей. Она определяется соотношением эквивалентных размеров пор и частиц взвесей - , величиной коэффициента , гидронапором жидкости, склонностью к набуханию частиц среды и адгезией.

Химико-физическую активность ( адгезия) частиц взвесей можно выразить коэффициентом к, теоретическое обоснование которого требует отдельного исследования для каждого химического состава взвеси.

Если размеры пор и частиц взвеси соизмеримы , то количество закрытых пор ( сокращение живого сечения) п , где к- вероятность условия . При равномерном распределении в однородном поровом пространстве время закупорки наступает быстро. Приближенно это время t.? Здесь Т – время просачивания для чистой жидкости при данном напоре. Отиетим , что пористость большинства горных пород колеблется в интервале 0,1 ( лавобрексия) – 0,85 ( туф).

При интенсивности подачи жидкости существенно большей скорости просачивания , жикость растекается по наружной поверхности пористой среды. Рассмотрим вопрос об общей скорости растекания . С учетом данных в работе [2] , скорость растекания по наклонной поверхности

V , (11)

где избыточная интенсивность ( разности скорости подачи и интенсивности впитывания), tg-параметр уклона поверхности стока. При достаточно малом периоде времени , где - время наступления фазы фильтрации и время впитывания, полная скорость растекания . Убывание напорного слоя жидкости на наружной поверхности среды h =Vt

Скорость стекания по уклону

, ( 12 )

где t – время подачи жидкости с избыточной интенсивностью.

Вероятность распределения частиц взвеси во времени по длине потока (глубине –h )для двухмерной среды = к, где d- размеры данной фракции и эквивалентный. Вероятность учитывает неодновременность попадания частиц взвесей полностью закрывающих поры слабонабухающей среды в начальный период времени. Для существенно набухающих сред закупорка пор происходит постепенно, если размеры частицы взвеси существенно меньше размеров пор. Глубина отложений взвеси имеет характер близкий к экспоненте и требует экспериментальной оценки.

В глинистых грунтах размерная фракция частиц менее 2мкм может составлять до 90% набухание достигается слабыми адгезионными силами ( теплота смачивания 10-25 ккал/моль), удаление обеспечивается температурой около 90.

Произведем расчетную оценку постоянных коэффициентов. Капиллярная сила Р_к=р. Эквивалентный радиус ( по Б.Дерягину ) r = e/S, где е — пористость, S — кинематическая поверхность: отношение поверхности частиц к объему тела. Для определения эквивалентного радиуса-rмалоглинистых грунтов может быть использована формула Козени ( на основании гранулометрического состава дисперсных пород)

Значение е можно определить экспериментально с помощью прибора Б. Дерягина по сопротивлению почвы разреженному потоку газа. Капиллярное давление, определенное по методу В. Г. Корнева, составляет для разных почвогрунтов величину порядка 1-10 МПа. Без учета частичной молекулярной адсорбции величина капиллярного давления определяется по величине поднятия столба воды h в слое пористой среды по формуле :

r= 2.

Значение коэффициента можно оценить, рассмотрев движение воды в вертикальной поре с учетом только гидравлических сопротивлений. В этой задаче Пуазейля, как известно, средняя скорость

. Здесь вязкость воды, H -предельная глубина пропитывания.

Из краевых условий при x = H, когда силы сопротивления Р и P_г уравновешиваются весом образовавшегося столба волы высотой H, имеем, как принято выше P_T+P_r=. Тогда .

С учетом полной влагоемкости W и начальной влажности w₀ ( в относительных долях) предельная высота впитывания h (глубина просачивания)

, где y - удельный вес твердой фазы.

В соответствии с принятым допущением, коэффициент

и коэффициент . Здесь р -начальное давление воздуха в почве (близко к атмосферному).

Для дисперсных пород типа супесчаных и глинистых грунтов можно принять значения характеристик при просачивании воды: вязкость = 10кгс/м, капиллярное давление р= 10Па, h = 0,5-1 м, W - = 0,3-0,6, r= 10м, y = 1500 – 2000 кг/м, интенсивность ( для дождевого орошения) м/с, . Для выбранных условий расчетные значения коэффициентов уравнений впитывания- просачивания имеют интервалы значений : b = кг/м, = 0,02 – 0,006 кг/с, величина коэффициента а = 10 кг/с. Важно отметить, что >> a. Капиллярная сила в расчете на пору может изменяться в широких пределах : Р = 10Н. Расчетные значения начальной и конечной скорости ( для принятых условий интенсивности притока воды и величин расчетных коэффициентов) составляют: V= (1-5)10м/с и V= 10м/с.

При средних величинах D = 10 1|c Глубина просачивания при ( t) h= (V . В общем случае величина h=.

Эксперименты проводились на плотных суглинистых грунтах с эквивалентным радиусом пор, рассчитанным по данным гранулометрического анализа на основании формулы Козени. При этом величина r= 10 h = 0,7м, показатели относительной влажности W = 0,71 и = 0,12, капиллярное давление по методу В.Корнева – р = 15 кПа, интенсивность капельно-дождевого орошения составляла 5- 20 мм/мин. Опыты проводились на трех типах суглинистых грунтов с определением изменения скоростей впитывания с интервалом времени от 1 до 120 мин при измерении соответствующих глубин просачивания . Опытная установка состояла из трубчатой колонны с прозрачными окнами – щелями по ее высоте . Экспериментальные и расчетные данные для конкретных данных имели удовлетворительное схождение по величине начальной и конечной скорости и экспоненциальному характеру впитывания . Осредненные опытные величины начальных скоростей (для грунта с величиной конкретного эквивалентного радиуса), представленные в практически более удобной размерности составляют 13 – 25 мм/ мин, соответственно, конечная скорость - 0,1 – 0,6 мм/ мин. Отклонение опытных и расчетных данных не превышало 15 -20%, что для подобных систем можно считать вполне корректным.

Полученные уравнения вполне удовлетворительно описывают процесс заполнения порового пространства твердой среды ( фазу впитывания), а частные решения уравнений впитывания -

процесс фильтрации ( при постоянной конечной скорости).

Коэффициенты расчетных формул напрямую связаны с конкретными свойствами пористого материала типа почвогрунтов ( гранулометрический состав, эффективный радиус пор, вязкость жидкости, капиллярное давление, влажность и влагоемкость и др.) Эти свойства определяются известными стандартными методами.

Литература

1. Заднепровский Р.П. К определению скорости просачивания воды в почвогрунты // Метеорология и гидрология , 1969, № 109. С. 69-75

2. Заднепровский Р.П. Рациональная скорость движения дождевальной машины //Механизация и электрификация сельского хозяйства, 1971, № 7, с.21-23

3. Фролов Ю. Г. Курс коллоидной химии. М:Химия, 1989,

С. 420-427

4. Ветренко Е.А. Аналитический подход к определению некоторых водно-физических характеристик почвогрунтов. Материалы межд. научно-практической конференции « Актуальные проблемы АПК» , Волгоград : ВГСХА, 2005. С.135-138

5. Заднепровский Р.П. Энергетические показатели межфазных процессов в глинистых породах и закономерности электродных потенциалов грунт-металл

// Геоэкология, инженерная геология , грунтоведение. 2005, №1. С.64-67

6. Ищенко Ю.А. Явление и технология дельта-фильтрования природных и сточных вод. Волгоград: ВГСХА, 1997, 209с