Математика

5. Математическое моделирование

Колеснікова Н.В.

Херсонський державний університет

Модель Морлі для згинних деформацій пластин

Постановка проблеми. Метод скінченних елементів – один з найбільш ефективних сучасних методів чисельного розв’язування інженерних і математичних задач. Для розрахунку згинних деформацій пластин методом скінченних елементів найбільш широко використовуються найпростіші скінченні елементи: прямокутний і трикутний.

Найпростіший можливий елемент для розв’язування задач про згин тонких пружних пластин був побудований Морлі наприкінці 60‑х років минулого століття [5]. Він показав, що, не дивлячись на достатньо очевидне порушення неперервності, отриманий при використанні цього елемента розв’язок збігається і співставляється за точністю з розв’язком, отриманим при використанні більш складних трикутних елементів.

За допомогою трикутних елементів можна ідеалізувати пластину будь-якої конфігурації, тому цей елемент дуже важливий для практичних застосувань.

Аналіз останніх досліджень. Функції форми та матриці жорсткості для трикутних елементів були побудовані Зенкевичем, Морлі, Сіє, Клафом, Точером, Айронсом, Аргірісом, Беллом, Боссардом, Віссером, Куппером, Батліном, Фордом [1, 2, 4].

До розв’язку пред’являються вимоги міжелементної неперервності функції та її похідних. Саме з цим пов’язані складності, що виникають при побудові функцій форми цих елементів.

У більшості практичних інженерних розрахунків точність, що досягається при використанні неузгоджених трикутних елементів, виявляється достатньо прийнятною. Найчастіше такі трикутники дають кращі результати, ніж еквівалентні узгоджені елементи [2, 3].

Формулювання цілей статті (постановка завдання). Альтернативою традиційному алгебраїчному підходу до побудови базисних функцій на дискретному елементі є простий, наочний і зручний геометричний метод. Тому особливий інтерес представляє вивчення можливостей геометричного моделювання базиса Морлі.

Основна частина.

Деформації згину пластин моделюються рівнянням Софі Жермен четвертого порядку (бігармонічне рівняння).

4

5

2

3

6

1

Для бігармонічного рівняння енергетичний функціонал містить другі похідні. На трикутнику визначимо квадратичну функцію за її значеннями у вершинах трикутника і за значеннями її нормальної похідної в серединах сторін.

Рис. 1 Трикутний елемент Морлі

При моделюванні неузгоджених елементів вимагається неперервність прогину у всіх точках на границі між елементами і співпадіння кутів нахилу у спільних кутах. Це завжди призводило принаймні до кубічного закону зміни . Якщо трохи послабити деякі з цих вимог, то з’являються цікаві можливості. Так для трикутника з 6 вузлами, у якості шести степенів волі якого прийняті значення в кутових вузлах і значення нормальної похідної у додаткових вузлах, визначається повний квадратичний поліном:

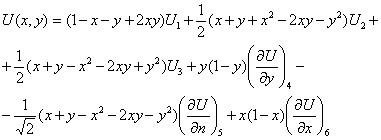
В результаті отримуємо найпростіший можливий елемент для задач про згин з постійними моментами і кривиною, еквівалентний трикутнику з постійною деформацією. Не дивлячись на достатньо очевидне порушення неперервності, отриманий при використанні цього елемента розв’язок збігається і співставляється за точністю з розв’язком, отриманим при використанні більш складних трикутних елементів. На думку Стренга і Фікса, ефективно використовувати не тільки неузгоджені, а й незбіжні елементи [4].

Важливою є задача візуалізації та дослідження функцій форми:

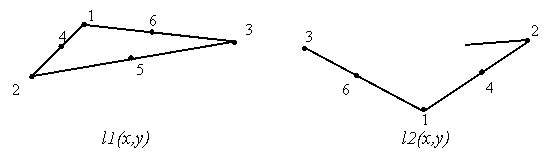
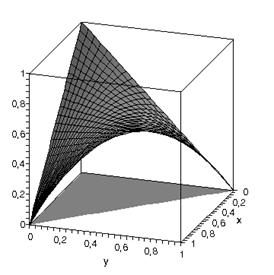
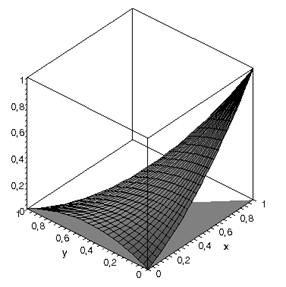
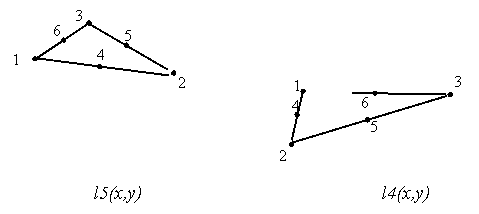
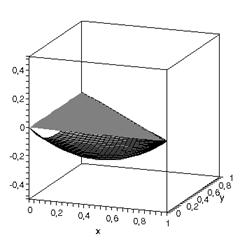
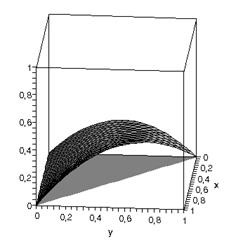
Рис.2 Функції форми елемента Морлі

Поряд з математичною перевіркою несумісних елементів кусочним тестуванням (Айронс і Раззак 1972 р.) використовують комп’ютерний експеримент. Елементи вважаються витримавшими кусочне тестування, якщо чисельний розв’язок відтворює відому відповідь з урахуванням помилок округлення [3].

Висновки. Проведено серію комп’ютерних експериментів для дослідження базисних функцій трикутника Морлі, а також вивчаються геометричні властивості базисних функцій за допомогою ліній рівня та площин , .

Література:

1. Галлагер Р. Метод конечных элементов. Основы. – М.: Мир, 1984. – 428 с.

2. Зенкевич О. Метод конечных элементов в технике. – М.: Мир, 1975. – 541 с.

3. Митчелл Э., Уэйт Р. МКЭ для уравнений с частными производными. – М.:Мир, 1981. – 216 с.

4. Стренг Г., Фикс Дж. Теория метода конечных элементов. –М. :Мир, 1977. – 349 с.

5. L.S.D. MORLEY, The triangular equilibrium element in the solution of plate bending problems, Aero. Quart., 19 (1968), pp. 149-169.