секция: «Технические науки»

подсекция 2

К.т.н. Похилько Л.К. , Бондаренко Ю.В.

Национальная металлургическая академия Украины

Днепропетровский национальный университет

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ НЕКОТОРЫХ ОТКЛОНЕНИЙ ФОРМЫ В УЗЛАХ ПОДШИПНИКОВ СКОЛЬЖЕНИЯ

Исследование влияния отклонений формы и расположения сопрягаемых деталей подшипников скольжения на величину критической толщины масляного слоя h_кр вызывает необходимость установления законов распределения отклонений формы и расположения как случайных величин.

Рассмотрим случаи отклонения формы цилиндрических поверхностей – отклонения от круглости и от цилиндричности.

В первом случае реальный профиль поперечного сечения цилиндрической детали может быть описан с помощью разложения ряда Фурье [1]:

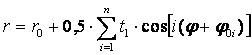, (1)

где r, - полярные координаты точек реального профиля;

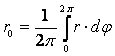– среднее значение радиуса профиля;

і – порядковый номер гармоники составляющей ряда ( і = 1...n);

t_{i ,} – амплитуда и фазовый угол i-й гармоники.

Первый член разложения указывает на наличие эксцентриситета средней окружности относительно центра системы координат.

Слагаемое с номером i = 2, а именно , представляет собой погрешность формы, называемую овальность (t₂ – величина овальности).

Последующие слагаемые с i > 2 – это отклонения формы, называемые огранкой, с числом граней, равным i.

В общем случае, отклонение от круглости представляется полным спектром накладывающихся друг на друга гармоник, однако на практике всегда имеет место доминирование одной из гармоник, составляющих ряд (1), что приводит к появлению частных видов отклонений от круглости – овальности и огранки [2]. Поэтому рассмотрим реальный профиль детали с учетом только доминирующей гармоники с номером i = m. Тогда форма реального профиля цилиндрической детали опишется так:

f_m = 0,5 t_m ·cos [m (φ + φ_om)]

В этом выражении величина t_m полностью характеризует отклонение от круглости в соответствии с принятым в ДСТУ 2498-94 определением.

Определим радиусы профиля детали в двух направлениях (рис.1), одно из которых выбрано произвольно, а другое - под углом π/2m к первому.

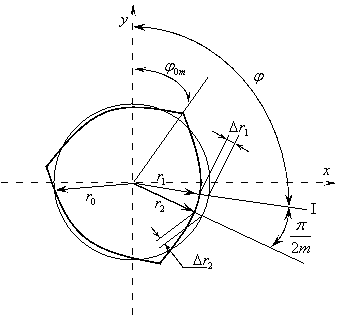
Рис.1. Определение отклонений поперечного сечения.

Тогда отклонения профиля ∆r₁ и ∆r₂ от средней окружности r₀

∆r₁= r₁ – r₀ = 0,5t_m cos [m (φ + φ_om)],

∆r₂= r₂ – r₀ = 0,5t_m sin [m (φ + φ_om)].

Умножив оба уравнения на 2, возведя их квадрат и сложив между собой, получим выражение отклонения от круглости t_m (амплитуда m-й гармоники).

.

Как размерные величины ∆r₁ и ∆r₂ распределены по закону Гаусса [2] с параметрами М(∆r) = 0; D(∆r) = σ₀², следовательно t_m является радиусом-вектором при двумерном нормальном распределении и подчиняется, как следует из теории вероятностей [3], закону Релея.

Аналогичные рассуждения можно провести и при анализе отклонений формы продольного профиля. При этом реальный профиль также может быть описан в виде ряда Фурье:

,

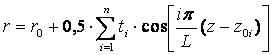где - прямоугольные координаты продольного профиля; i – порядковый номер составляющей гармоники; L – длина профиля; - амплитуда и фазовое расстояние i-той гармоники; - средний радиус профиля.

Первый член гармонических составляющих (i=1):

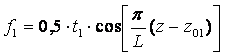
можно рассматривать, как наклон образующей – конусообразность: прямая () или обратная ().

Второй член разложения (i = 2):

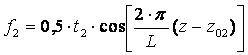
дает аналитическое описание седлообразного () либо бочкообразного () продольного профиля вала.

Аналогично определяем отклонения радиусов ∆r₁ и ∆r₂ в двух направлениях, расстояние между которыми равно (k – номер доминирующей гармоники), одно из направлений выбрано произвольно (рис.2).

Откуда следует, что частные виды отклонений формы профиля продольного сечения (конусообразность, седлообразность, бочкообразность) также подчиняются закону Релея.

Рис. 2. Определение отклонений продольного сечения

Литература

1. Ляндон Ю.Н. Функциональная взаимозаменяемость в машиностроении.-М.: Машиностроение, 1989.

2. Справочник по производственному контролю в машиностроении / Под ред. А.К.Кутая.- М.: Машиностроение, 1974.

3. Приборостороение и средства автоматики / Под ред. А.Н. Гаврилова.-М.: Машиностроение, 1993.