Д.С.
Куракбаев, Г.А. Палманова
Южно-Казахстанский
государственный университет им. М. Ауезова
СОЗДАНИЕ КОМПЛЕКСА ПРОГРАММ ПО ДИСЦИПЛИНЕ «ЧИСЛЕННЫЕ МЕТОДЫ»
В данной
работе создан комплекс программ для приближенных методов: решения
алгебраических и трансцендентных уравнений, решения систем алгебраических
уравнений, метода наименьших квадратов, приближенных методов вычисления
определенных интегралов и численного решения обыкновенных дифференциальных
уравнений. После запуска программы окно программы имеет следующий вид (рис. 1):
Рис. 1. Окно формы «Численные методы»
Здесь изображена информация о комплексе программ.
Нажимаем на кнопку Далее, которая находится в нижней части окна. После этого
откроется следующее окно программы
(рис. 2):
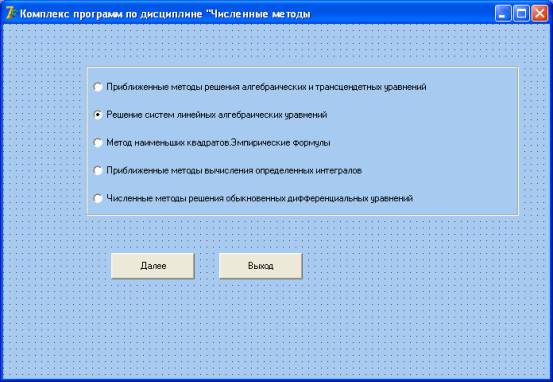
Рис. 2. Комплекс программ по дисциплине «Численные методы»
В появившемся диалоговом окне пользователю будет
предложен комплекс программ по дисциплине «Численные методы» (рис.2), из
которого выбираем «Решение систем линейных алгебраических уравнений». В появившемся окне
выбираем метод Гаусса. В окне программ
пользователю будет предложено ввести размерность (например 3) системы линейных
алгебраических уравнений (рис. 3).
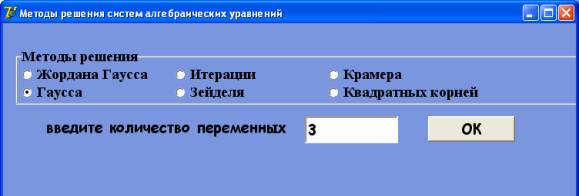
Рис. 3. Методы решения
систем линейных алгебраических уравнений
На этом этапе доступно только поле ввода размерности и
OK. Щелчок по этой кнопке открывает таблицу, которая
предназначена для ввода матрицы коэффициентов и вектора правых частей системы
уравнений. После ввода данных доступными становятся кнопки Решение и Выход (рис. 4)
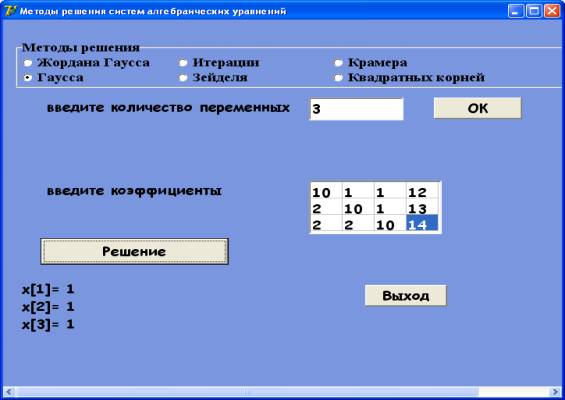
Рис. 4. Решение систем линейных алгебраических уравнений
методом Гаусса
Щелчок по кнопке Решение открывает таблицу, в которой
пользователь может увидеть решение данной системы (рис. 4). Кнопка Выход прекращает выполнение программы.
Если выбираем метод Зейделя или метод Итерации,
то появится поле для дополнительного ввода данных eps, который
используется для точности решения систем линейных алгебраических
уравнений (рис. 5) и нажимаем – OK, тогда в окошечке появится разбитая на клетки таблица
в которую следует внести коэффициенты систем уравнений. Далее нажимаем на кнопку Решение и тогда ниже появятся
результаты вычислений.
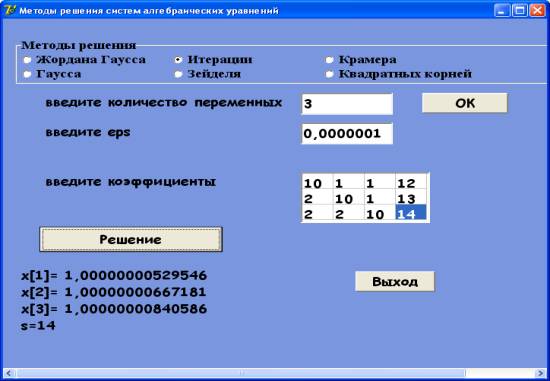
Рис. 5. Решение систем линейных алгебраических уравнений
методом
итерации
При выборе кнопки «Приближенные методы решения алгебраических и трансцендентных
уравнений»
откроется окно программы. В этом окне изображены кнопки «Отделение корней уравнений», «Метод
половинного деления», «Метод хорд», «Метод касательных», «Комбинированный
метод» и «Метод итерации». Для определения количества и интервала нахождения
корней уравнений выбираем кнопку «Отделение корней уравнений». На экране
появится запрос об уравнении, границах нахождения корней уравнения и шаг
(например задавая функцию f(x), А=-100, В=100, h=0.1), тогда при помощи
комплекса программ можно установить возможно тесные промежутки, в которых
содержится один и только один корень, а также количество корней уравнения.
Далее выбирая одну из вышеприведенных методов можно уточнить корни, т.е.
довести их до заданной степени точности (например задавая f(x), f1(x), f2(x), А, В, EPS).
Если в
результате эксперимента были получены некоторые данные зависящие от x и y, тогда
используя метод наименьших квадратов построим аналитическую зависимость 
, наиболее близко проходящую к экспериментальным точкам.
Задача
подбора экспериментальной зависимости методом наименьших квадратов состоит из
двух этапов: на первом этапе по экспериментальным данным выбирается вид
зависимости (прямая, парабола, и т.д.), на втором этапе подбираются параметры
выбранной зависимости.
В
созданном комплексе программ имеется программа «Метод наименьших квадратов» при
выборе которого в окне программ появится кнопки «Метод наименьших квадратов для
линейной зависимости» и «Метод наименьших квадратов для параболической
зависимости». При выборе одного из них в окне программ пользователю будет
предложено ввести количество проведенных экспериментов (например, n = 10), после нажатия
кнопки OK в окошечке появится разбитая на клетки таблица, в
которую следует ввести экспериментальные данные x и y, затем нажимаем на кнопку Решение
тогда в окне решении появится результаты вычислений.
Используя комплекс программ можно приближенно вычислить определенные
интегралы при помощи формул левых и правых прямоугольников, формул трапеции,
Симпсона, Гаусса, Чебышева, а также формул А.А. Маркова 1, 2. При нажатии
кнопки «Формула
Чебышева» откроется окно запроса. Здесь задаем в поле значений интегрируемую
фукцию f(x) (для задания
функции используется функция EVALUATE() –
которая вычисляет значения выражения, представленного в символьном виде),
А(нижняя граница интеграла), В(верхняя граница интеграла), N(количество узлов и коэффициентов квадратурной формулы
Чебышева), EPS (точность вычисления
интеграла). При нажатии кнопки Вычислить комплекс программа приближенно вычисляет определенный интеграл с
заданной точностью, а в окне результатов появляется численное значение расчета.
Аналогично можно использовать комплекс программу для вычисления определенных
интегралов вышеприведенными квадратурными формулами.
Если
выбрать кнопку «Численные методы решения обыкновенных дифференциальных уравнений», то
откроется окно программы: «Метод Эйлера для решения задачи Коши», «Метод Рунге
- Кутта для решения задачи Коши», «Решение обыкновенных дифференциальных
уравненй 2-го порядка методом сеток», «Решение обыкновенных дифференциальных
уравненй 4-го порядка методом сеток». При выборе метода Рунге – Кутта откроется
окно запросов. Задаем в поле значений функцию f(x), p(x), q(x) (для задания
функции используется функция EVALUATE() –
которая вычисляет значения выражения, представленного в символьном виде), х0,
у0 (из начального условия задачи) h
(достаточно малый шаг) и N (количество
точек деления), при нажатии кнопки Вычислить комплекс программа
приближенно решает задачу Коши, а в окне результатов появляется численное
значение расчета. При выборе кнопки «Решение обыкновенных дифференциальных уравненй 2-го
порядка методом сеток» решается следующая линейная краевая задача:
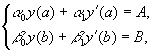
где p(x), q(x), f(x) – известные непрерывные на отрезке [a, b] функции, 
- заданные
постоянные, причем 
и 
Задавая в поле
значении y0, y10, YN, Y1N, A0, A1, A, B0, B1, B, p(x), q(x), f(x) (в символьном
виде) и N при нажатии кнопки Вычислить
комплекс программа приближенно решит вышеприведенную краевую задачу второго
порядка.
В работе численно обоснована применимость
разработанных алгоритмов и программного комплекса на тестовых примерах. Можно
говорить, что задача от её возникновения до решения проходит через некоторую систему,
состоящую из людей, решающих задачу. Решение задачи особенно замедляется в
случае, когда решением задач занимаются представители конкретных наук, например
экономисты, машиностроители, экологи, строители, малознакомые с элементами
численных методов или программирования. Поэтому в настоящей работе создан
комплекс программ с максимально простым обращением предполагающих малую
квалификацию пользователя.
Литература
1. Демидович Б.П., Марон И.А. Основы
вычислительной математики. -М.:
Наука, Главная редакция физико - математической литературы, 1970.
-664с.
2. Мысовских И.П. Лекции по методам вычислений. – М.:
Физматгиз, 1962.
-344с.
3. Крылов В.И.
Приближенное вычисление интегралов. –М.: Наука, 1967.
-500с.
4. Зубов В.С. Программирование на языке TURBO PASCAL .
Версии 6.0 и
7.0. –М.:
Информационно - издательский дом Филинь, 1997. -320 с.
5. Фаронов В.В. Основы Турбо Паскаля. –М.: МГТУ,
-1992. -223с.
6. Чеснокова О.В. Delphi 2007. Алгоритмы и программы. /Под. общ.
редакцией Алексеева Е.Р. –М.: НТ Пресс, -2008. -368с.
7. Омельченко Л.Н., Шевякова Д.А. Самоучитель Visual FoxPro
9.0. –СПб.:
БХВ –
Петербург, 2005. -608с.