Magnetization, chemical potential and entropy of degenerate

                    relativistic electron gas in a strong magnetic field

                                                     V.V. Skobelev

                    Moscow State Industrial University, E-male: v.skobelev@inbox.ru 

Abstract. In the paper paradoxical properties of degenerated electron gas in a strong magnetic field  , in which electrons are on the ground Landau level, are studied. Namely, we obtain, that magnetization decreases with increase of magnetic field, and on the contrary, increases with temperature increase. From our point of view, it is possible to explain this phenomenon effective reduction of space in a strong magnetic field from three-dimensional to one-dimensional (along the field).

          Originally interest to research of magnetic properties of electron gas was stimulated by investigation of metal’s magnetism, which magnetic properties are substantially caused by nonrelativistic electron gas, and with a big degree of accuracy it is possible to consider them as ideal Fermi-gas.    Thus the electron spin magnetic moment causes paramagnetic properties (Pauli’s paramagnetism[1]), and transverse in relation to a field quantum excitation levels-diamagnetic properties (Landau’s diamagnetism[2]).

  With opening of neutron stars-pulsars was an additional stimulus for research of magnetic properties of electron gas, as in them it is essentially relativistic[3],besides being in a superstrong magnetic field of the star[4], therefore, as it will be visible, magnetic properties of electron gas radically change. In the present paper we calculate magnetizationof degenerate relativistic electron gas, and analyze their field induction and temperature dependence, which appears to be extremely unusual.

   The maximum information one can obtain from- potential: 

                                                 ,                                                                (1)

where the sum is over all quantum stateswith energy, andis chemical potential. In our case of constant and homogeneous magnetic field the sum may be presented in a form [5]:                   

                                  ,                                                                                     (2)

where,is an elementary charge,is the momentum along the field,is the numbers of Landau’s states,is the spin statistical weight. Electron energy is equal 

                                     .                                                                (3)

For the further we will notice that according to expression (2) electron concentration is defined by relation

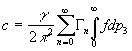                                             ,                                                                          (4)

where

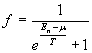                                                -                                                                                    (4à)

is Fermi-Dirac’s distribution function. Further we are interested in a case of strong magnetic field, when main contribution to the sum comes from the ground Landau level. In the case of totally degenerated electron gaswe obtain

                                                ,                                                                                      (5a)

that is Fermi momentum

                                                 ,                                                                                   (5b)

or in dimensionless variables,

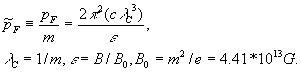                                                                          (6)

From the expression (3) it is evident, that levelsdo not energize, if,or

                                                               ,                                                                             (7)

and in more convenient kind:

                                                                 .                                                  (7a) 

   From the differential relation for-potential [5]  

                                              ,                                                     (8)

whereis a total magnetic moment,-magnetization, follows, that 

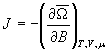                                                  ,,                                                         (9a)

and entropy per unit volume

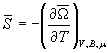                                           .                                                                                 (9b)

Taking into attention (1), (2) we have for:

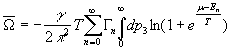                                     .                                                      (10)

Assuming satisfied a condition (7), and integrating by parts, we receive for the contribution:                                    

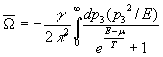                                           ,                                                                 (10a)

where. For the totally degenerated gas with notations one can obtain in dimensionless variables:                        

                                         .                                    (11)

   Using (9a), we find magnetization of the totally degenerated electron gas:

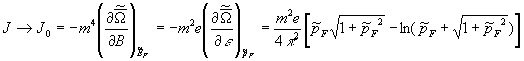      .            (12)

In the nonrelativistic limitthis expression is reduced to

                                      ,                                                                                     (12a)

and in ultrarelativistic case-

                                       .                                                                                     (12b)

Apparently from (12),(12a,b),(6) dependenceon a field is essentially nonlinear, and magnetization decreases with field grows. One can explain this unusual result in the following way.  The electron wave function on the ground Landau level is proportional to exponential factor [6,7]                                               

                                                            ,

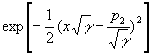 where quasimomentumdefines the position of the wave package center. Choosing for simplicity, we rewrite this factor as . It means, that electron is located in the region, and with a field grows it decreases. Further, our approximation of ideal Fermi-gas may be realized, as for a classical gas, a) or  in a case of low concentration, b) or in a case of  very small sizes of particles (that is their localization regions) . In both cases we have rarefied ideal gas. From here actual equivalence of this  ways of ideal electron gas reception follows. To this requirement  formulas (6), (12), (12a,b) satisfy. In particular,  in according with (12a,b),magnetization decreases or with concentration reduction, or, as it follows from mentioned equivalence, with field grows.

 It is of interest to calculate the temperature corrections toand the meaning of entropy of ideal electron gas in strong magnetic field. Let’s use for this asymptotic expansion [5]:

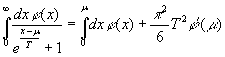
                                                     ,                                       (13)

and preliminary make in the formula (10a) variable replacement

                                        .                                                                                (13a)

Then it becomes

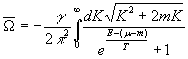                                                  .                                                      (14)

The integral has the form (13), if we put in it:

                                                  .

Thus, expression (14) with square-law accuracy on temperature is equal

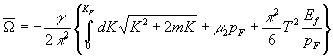                                  ;                               (15)

 a second term in figure brackets appeared at expansion of the first integral in (13) in temperature row , and the first term is a zero contribution in a temperature expansion and leads to expression (11) again.

  For determination(the total contribution of two last terms in (15)) it is necessary to calculate. For this aim in formula (4) we must take onlycontribution and then make variable replacement (13a),after that it becomes

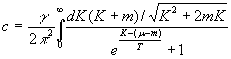                                             .                                             (16)

     By expansion in temperature row (13) in analogous (15) manner we obtain:  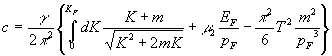                                                                                                                                                                                                                                                   .                                        .                     (17)

First integral leads to expression (5b) for Fermi- momentum again, and last two terms in figure brackets must compensate, because concentration does not depend on temperature. From this condition we find: 

                                                 .                                                                     (18)

On the contrary, “three- dimensional” case [5,8], in our “one-dimensional” case(7a). By substitution of eq. (18) into (17) we obtain for temperature contribution to-potential:

                                                   .                                                              (19)

Correspondingly, taking into account (11), we find for dimensionless-potential:

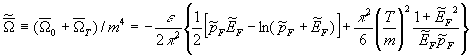                        ,     (20)

whereis defined by (6).   

In according with (9a) we find for magnetizationwith temperature correction:          

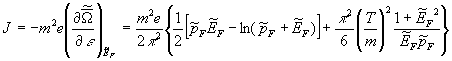                       .          (21)      

Apparently, in a strong magnetic field, that is in “one-dimensional” case, there is one more feature in dependence ofon parameters – with temperature   increasetoo grows.  This, at first sight, strange result  is possible to explain  as follows. Namely, negative sign of leads to a positivity (12), that is to a paramagnetism of electron gas, how should take place, as in the absence of transverse excitations Landau’s diamagnetism too , naturally, is absent, and spin paramagnetism  dominates [1]. On the other hand, the same signmay be explained by signand demand of entropy positivity (note, that only the last term in (15) contribute to derivative, because there takes place at constant)  

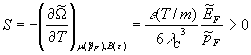                                        .                                               (22)

Thus, the “anomalous dependence”, as well as, actually follows from the physical reasons. We will discuss now the possibility of realization of effects under consideration in laboratory conditions. In this case for one-valent metals[9]and from (7a) follows that. But such fields  exist unless in white dwarfs [10], but in any way in laboratory conditions. Further, in white dwarfs [11], and  value of critical field is, so the considered effects again can’t be realized . And only in neutron stars, in whichand[7],”on a limit” necessary conditions take place [12], but “our” effects would not have, obviously, observable consequences. Thus, in situations known to us the anomalous behavior is out of observation. But it is not excluded that corresponding fields may be realized in laboratory conditions in the long-term future.      

            

 

 

 

      

 

 

 

 

                                   References:                                                                        

1.      W. Pauli, Z. Physik, V.41,P. 81, 1927.

        2. L.D. Landau, Z. Physik, V. 64,P. 629, 1930.

       3  .S.Weinberg, Gravitation and Cosmology, Massachusetts Institute of Technology, John Wiley and Sons, Inc., 1972.

       4  Dall’OssoS., Shore S.N., Stella L., Mon. Not. Asron. Soc., V.398, P.1869 (2009).

 5.L. D. Landau and E.M. Lifshitz, Course of Theoretical Physics, Vol.5: Statistical Physics: Part I,  Butterworth-Heinemann, Oxford,2000.

  6. L.D. Landau and E.M.Lifshitz, Course of Theoretical Physics, Vol.3: Quantum Mechanics: Non-Relativistic Theory ,Butterworth-Heinemann, Oxford, 1977.

 7. V.V. Skobelev, JETP, V. 113, P. 792, 2011.

 8. L. Homorodean, Int. J. Mod. Phys. B, V.13,P. 3133, 1999.

 9. S.V. Vonsovski, Magnetism (in Russian), Moscow, Nauka, 1984.

 10. A.T. Potter and C.A. Tout, arXiv:0911.3657 [astro-ph.SR].

 11. S.Shapiro and S. Teukolsky, Black Holes, White Dwarfs, and Neutron Stars, Wiley, New York, 1983.    

        12.  R.C. Duncan and C. Tompson, Astron. J.,  V.392, P.L9, 1992.