Сельское хозяйство/
Механизация сельского хозяйства
К.т.н. доцент Щербаков Н.В., ст. преподаватель Ким С.А.,
ст. преподаватель Галямова А.А.
Костанайский государственный университет им. А. Байтурсынова, Казахстан
Моделирование работы
широкозахватного культиватора
При совершенствовании и создании широкозахватных почвообрабатывающих
орудий исходим из того, что их производительность должна быть максимальной
(W→max), ширина захвата (В) и
скорость движения (V) – оптимальными (В и V→опт), при минимальных дифференциальных затратах (Uдиф→min)
и номинальной загрузке двигателя с учетом неустановившегося режима его работы. Обеспечение
высокой производительности и качественной обработки почвы возможно при
устойчивом движении орудия по глубине, т.е. их колебания в
продольно-вертикальной и поперечно-вертикальной плоскостях, должны быть минимальными:
(1)
где:
- конструктивные параметры орудия, м;
- массы и моменты инерции;
-
коэффициент жесткости и динамические коэффициенты сопротивления опорных колес и рабочих органов;
-
возмущающие воздействия от неровностей поверхности поля и неравномерности
сопротивления почвы.
В данном случае возникает необходимость в более полном математическом
описании изучаемых процессов с учетом взаимосвязи между динамикой движения
агрегата, характеризующей прежде всего устойчивость орудия по глубине
обработки, и дифференциальными затратами, учитывающими вместе с качеством
обработки энергетические показатели работы. Для теоретического рассмотрения
функционирования агрегата воспользуемся
моделью приведенной на рисунке 1. [1]
В данной модели входными возмущениями
являются неровности поверхности поля 
и неравномерность сопротивления почвы 
, а выходными критериями – среднеквадратическое отклонение
глубины обработки 
и
дифференциальные затраты Uдиф.
Динамика работы орудия определяется
операторами Wh и WR, зависящими от
конструктивных параметров 
и коэффициентов 
, характеризующих систему культиватор-почва.
Оператор Wб определяет влияние качества обработки почвы на
дифференциальные затраты и зависит от ширины захвата орудия В, скорости движения V и
коэффициентов ρ, m, n,….
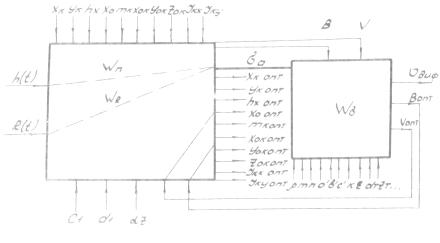
Рисунок 1. Модель функционирования
почвообрабатывающего агрегата
Таким образом, зная операторы Wh,
WR, Wб, можно определить оптимальную ширину захвата орудия Вопт и скорость движения V опт,
минимизируя дифференциальные затраты Uдиф→min.
Для оптимального сочетания ширины и скорости орудия, задаваясь начальными
значениями основных конструктивных параметров, можно последовательно оптимизировать
, минимизируя критерии 
и Uдиф.
Моделирование
широкозахватных шарнирно-секционных почвообрабатывающих орудий рассмотрим на
примере культиватора , состоящего из центральной секции и шарнирно соединенных
с ней поперечными брусьями рамы боковых секций, установленных под углом к
направлению движения рабочих органов.
Причем внутри рамы каждой боковой секции размещена дополнительная
секция, шарнирно соединенная с ее поперечными брусьями (рисунок 2). Для
описания движения орудия выбираем инерциальную систему координат πXYZ с началом в мгновенном центре
вращения подвижной системы координат 0'X'Y'Z', 0"X"Y"Z",
0"'X"'Y"'Z"', жестко связанные с секциями орудия (рисунок
2,3,4).
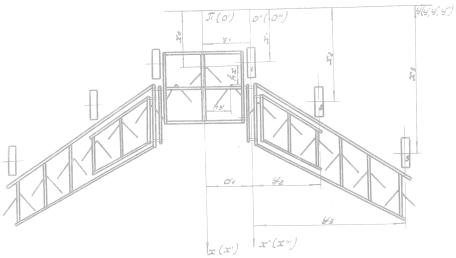
Рисунок 2. Расчетная схема
почвообрабатывающего орудия
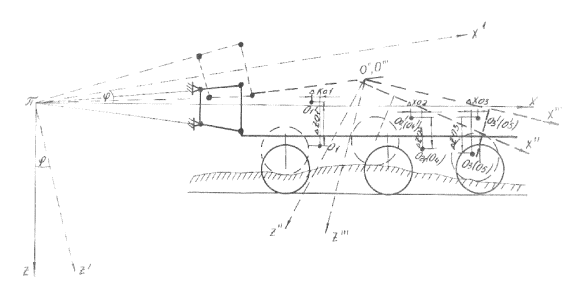
Рисунок 3. Перемещение системы в
продольно-вертикальной плоскости
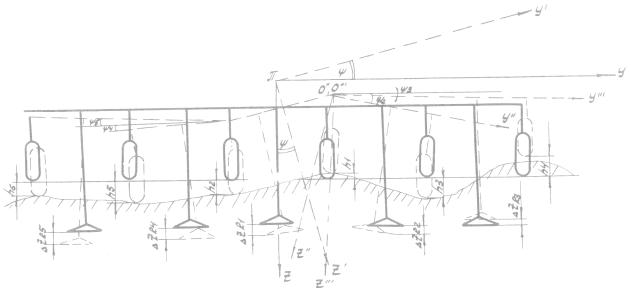
Рисунок 4. Перемещение системы в
поперечно-вертикальной плоскости
При определении операторов Wh и WR
культиватора-плоскореза с учетом общепринятых допущений [2] используем уравнение
Лагранжа II рода в виде:
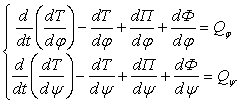(2)
где: 
– кинетическая
энергия орудия;
- потенциальная
энергия;
- функция сопротивления;
и 
- обобщенные силы,
соответствующие обобщенным координатам
и 
, (рисунок 3, 4).
Кинетическая энергия орудия определяется
по формуле:
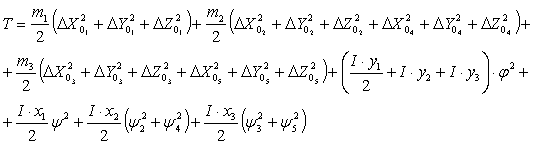(3)
где: 
- масса секций;
- перемещения центров
тяжестей секций;
- моменты инерций
секций.
Потенциальную энергию находим по формуле:
(4)
где:
- жесткость опорных колес орудия;
- вертикальные
перемещения колес центральной секции.
Функция сопротивления системы равна:
(5)
где:
- коэффициент демпфирования колес;
- коэффициент
сопротивления почвы вертикальным перемещениям рабочего органа;
- вертикальные перемещения центров сопротивления отдельных секций орудия.
Обобщенные силы находим из соотношений:
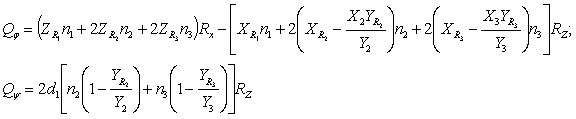(6)
где:
- координаты центров сопротивления секций орудия;
- неравномерность
сопротивления почвы продольному и вертикальному перемещению рабочего органа.
Дисперсия
глубины обработки i-м рабочим органом центральной секции определяется
следующим образом
внутренних боковых секций:
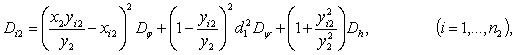
внешних боковых секций:
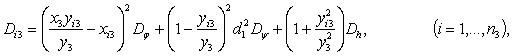
где: 
- дисперсия рельефа и
углов φ и ψ [3]
- координаты рабочих
органов секций.
Устойчивость глубины обработки всего орудия оценивается величиной
среднеквадратического отклонения секций:
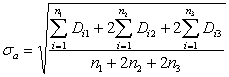(7)
Используя [4], определим стоимость потерь урожая:
(8)
где:CП –
закупочно-сдаточная цена продукции, тнг /га;
U –
урожайность культуры, т/га;
U0
– урожайность зерновых культур при
оптимальном качестве обработки почвы, т/га;
КП – коэффициент
учета потерь урожая от растягивания сроков уборки, 1/ч;
F –
объем работы, га.
Урожайность культуры в зависимости от среднеквадратического отклонения
глубины обработки аппроксимируется выражением:
(9)
где:
-
среднеквадратическое отклонение глубины обработки, м;
A, a, B, b
- коэффициенты аппроксимации.
Используя математическую модель и экспериментальную
установку, проводили исследования по
изучению влияния расстановки рабочих органов по ходу на качество работы орудия.
[5]
В качестве оценочного критерия при анализе
принимали среднеквадратическое
отклонение колебания орудия от положения равновесия в продольно-вертикальной
плоскости (рисунок 5).
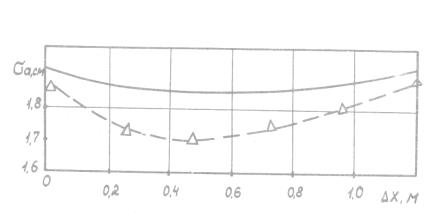
Рисунок 5. Влияние расстановки рабочих органов по ходу
движения (Δx) на устойчивость орудия по глубине обработки
(σа)
- теоретическая кривая; Δ--Δ-
экспериментальная кривая.
Гипотеза об адекватности модели проверялась
методом корреляционного анализа по выборочному коэффициенту r и
подтвердилась (r =0,9) при
доверительной вероятности ρ=0,95 [5].
Таким образом, пользуясь изложенной методикой и принципиальной схемой
почвообрабатывающего орудия как базовой, можно обосновать основные параметры
широкозахватных орудий по качеству обработки почв.
Литература
1. Щербаков
Н.В., Ким С.А. Моделирование технологического процесса внесения минеральных удобрений. - Вестник
науки КГУ 2002.
2. Паскаль С.Р.,
Грибановский А.П. Устойчивость хода культиватора – плоскореза по глубине. –
Механизация и электрификация сельского хозяйства, 1982, №6.
3.Шульгин И. Г. и др.
Методика обоснования основных параметров и режимов работы широкозахватных
почвообрабатывающих противоэрозионных орудий. – Сборник научных трудов НПО
«Целинсельхозмеханизация»
Алма-Ата 1985.
4. Саклаков В.Д.,
Сергеев Н.К. Технико-экономическое обоснование выбора средств механизации. – М.
Колос. 1973.
5. Иванова В.И., и др.
Математическая статистика. – М. Высшая школа, 1981.