Калиев
Б.К., Болат Е.Б.
Костанайский
государственный университет им. А.
Байтурсынова, Республика Казахстан
Применение статистических методов исследования зерновой массы
Гидротермическая
обработка зерна оказывает благоприятное воздействие на технологические свойства
зерна, его питательную ценность и потребительские достоинства крупы.
Гидротермический обработанная
масса зерен крупы является статистической системой, так как число зерновок (то
есть число математических событий) очень значительно, а их распределение в
занимаемом объеме носит случайный характер, что позволяет применять статистические методы.
Поэтому в этом случае можно применить статистические
методы исследования, например выборочный метод с вычислением показателей колеблемости
изучаемого признака.
Эти показатели могут являться показателями степени
однородности или неоднородности выборки, а из дальнейшие исследования дадут
возможность сделать вывод о применении
полученных результатов на всю совокупность, то есть партию зерна [3].
Ряд исследователей основным критерием,
характеризующего качество мелкодисперсной смеси принимают среднеквадратическое
отклонение S или дисперсию S2 содержания ключевого компонента в пробах [1, 2]. Между
тем, наиболее распространенным критерием в большинстве отраслей промышленности
принят коэффициент вариации (неоднородности) V.
В качестве характеристики муки и мучной
композиционной смеси в мукомольной отрасли применяется показатель белизны,
поэтому предлагается цели принять коэффициент его вариации [3].
Если коэффициент вариации меньше 10% -
вариация или неоднородность массы незначительная и она удовлетворительного
качества, а при больших значениях она признается неоднородной и
неудовлетворительного качества. В агротехнических исследованиях принято
считать, что, если коэффициент вариации менее 10%, то она незначительная, если
она более 10%, но менее 20%, то такая изменчивость среднего уровня и
значительная, если коэффициент вариации более 20% [3].
Способ определения однородности мучных
смесей в пищевых производствах состоит в нахождении коэффициента вариации из не
менее десяти проб отобранных из смесителя в различных местах, либо на выходе из
него через определенные промежутки времени [3].
Опираясь на приведённый выше анализ, можно
сделать вывод о том, что, приняв за одну из основных характеристик крупы ее
цвет, в качестве параметров качества можно использовать среднеквадратичные
отклонения Sх, Sу,
дисперсию Sх2, Sу2 и коэффициенты вариации Vх, Vу его координат, при этом предельные значения
последних, определяющие зерновую массу как однородную, можно ограничить по
аналогии с пищевыми производствами 10-ю процентами. Если с помощью коэффициента
вариации можно оценить степень неоднородности зерна или крупы, то величиной М=(100–V)% – наоборот, степень их однородности.
Приведем формулы для определения
вышеуказанных параметров при сгруппированных значениях координат цвета ху:
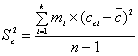 , (1)
, (1)
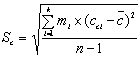 , (2)
, (2)
![]() , (3)
, (3)
где ![]() – среднее значение координаты х или у, равное
– среднее значение координаты х или у, равное
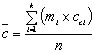 , (4)
, (4)
где сci –
середина i-го интервала для координаты х или у;
mi – число
измерений в i-м интервале;
k –
число интервалов для координаты х или
у;
n –
общее число измерений, равное ![]() .
.
Наиболее полное описание цвета зерна можно
получить построением трехмерных распределений треххроматических координат цвета
XYZ или
значений RGB-составляющих на цветовом треугольнике модели CIE, которые при нормальном распределении каждой составляющей
представляли бы эллипсоид равной плотности. Учитывая преимущества
«плоскостного» представления цвета в координатах ху цветовой диаграммы CIE xyY, полное описание цвета зерна
или крупы можно получить построением двумерного распределения этих координат.
При нормальном распределении каждой координаты цвета и наличии линейной
корреляционной связи между ними плотность совместного двумерного распределения Р(х,у) определяется
выражением
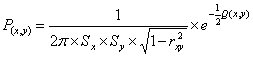 , (5)
, (5)
здесь
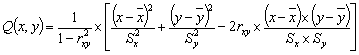 . (6)
. (6)
где rху –
линейный коэффициент
корреляции х и у, определяемый по формуле
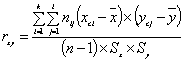 (7)
(7)
где xci, ycj – серединного i-го и j-го интервалов соответственно для координат цвета х и у;
![]() ,
, ![]() – средние значения
координат цвета х и у соответственно;
– средние значения
координат цвета х и у соответственно;
k, l – число интервалов соответственно координаты цвета х и у;
nij – число совместных наблюдений значений x и y.
Подтверждением наличия корреляционной
связи между координатами цвета ху
представляет определенный интерес, при этом предпосылкой к линейному характеру
этой связи может служить доказательство нормальности распределения координат
цвета. Другие виды корреляционной связи между координатами цвета предопределяет
различные выводы о степени изменения как тона цвета, так и его оттенков.
Количественно эту связь можно установить построением регрессионной модели на
основании статистической обработки результатов измерений координат цвета.
Литература:
1. Бобков В.А.
Анализ однородности мучных композиционных смесей по показателю белизны //
Хлебопродукты. – 2005. – №5. – С. 57-59.
2. Ликеш И., Ляга
Й. Основные таблицы математической статистики - Финансы и статистика, 1985. -
356 с.
3. Венецкий И.Г.,
Венецкая В.И. Основные математико-статистические понятия и формулы в
экономическом анализе – М.: Статистика,
1979. – 147 с.