Калиев
Б.К.
Костанайский
государственный университет им. А.
Байтурсынова, Республика Казахстан
Определение параметров исследования зерновой массы
При исследовании процессов
происходящих при гидротермической обработке зерна гречихи число зерновок нами рассматривается
как число математических событий и применяется выборочный метод статистического
исследования с вычислением показателей
колеблемости изучаемого признака.
В ходе исследований нами сделан вывод, что
приняв за одну из основных характеристик крупы ее цвет, в качестве параметров
качества можно использовать среднеквадратичные отклонения Sх, Sу, дисперсию Sх2, Sу2 и коэффициенты вариации Vх, Vу его координат, при этом предельные значения
последних, определяющие зерновую массу как однородную, можно ограничить по
аналогии с пищевыми производствами 10-ю процентами.
Присутствие корреляционной связи между координатами
цвета может подтвердится, в этом случае следует выяснить при анализе нескольких
выборок и однородность коэффициентов корреляции, что позволяет подтвердить или
опровергнуть предположение об однообразии процессов, происходящих при окраске
зерна с использованием исследуемых способов гидротермической обработки, то есть
об их идентичности. Для этой цели может быть применён Z-критерий
существенности различия любых двух коэффициентов корреляции, рассчитываемый по
формуле
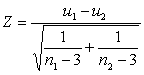 (1)
(1)
где
n1 и n2 – объемы соответствующих выборок, а u1 и u2 –
параметры преобразования Фишера, определяемые в общем случае по формуле
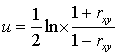 . (2)
. (2)
Если |z| при альтернативной гипотезе ρ1≠ρ2
(ρ1, ρ2 –значения
коэффициентов корреляции для генеральных выборок окажется меньше теоретического значения Z1-α/2, найденного из таблицы для вероятности P1-α/2 и уровне значимости a=0,05 то гипотеза о равенстве
коэффициентов корреляции принималась. В этом случае можно считать, что выборки
взяты из общей совокупности.
Отнесение таких распределений к нормальному
проверяется параметром χ2,
вычисляемым по формуле
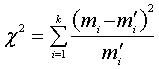 (3)
(3)
где mi
– наблюдаемые фактические частоты;
m¢i
– частоты, рассчитанные по нормальному закону;
k –
число пар, наблюдаемых и рассчитанных частот, которые сравниваются друг с
другом.
Распределение каждой координаты цвета в
отдельности в соответствии с теорией многомерных распределений предопределяет и
нормальность двумерного распределения. С другой стороны, такие индивидуальные
распределения координат цвета будут хорошо иллюстрировать состояние системы
зерен как наиболее однородное по сравнению со случаями, когда эти распределения
будут иными.
Индивидуальные распределения координат
цвета будут хорошо иллюстрировать состояние системы зерен как наиболее
однородное по сравнению со случаями, когда эти распределения будут иными.
Затем, находя из
таблиц при числе степеней свободы n–1 значение c2Т [4] сравнивают
его с расчетным. Если последнее меньше, чем полученное из таблиц для a=0,05,
то можно заключить с 5%-ой вероятностью совершение ошибки, что распределение
частоты появления зерен по цвету является нормальным.
Мерой упорядоченности, а значит и однородности сложной
случайной системы, к которой, как указывалось выше, относится и масса зерна или
крупы, может явиться также величина полной энтропии Н(у/х) для координат цвета х
и у, которую можно определить по
формуле [2]
![]() , (4)
, (4)
где Рij –вероятность любого возможного состояния системы
зерен;
Р(уj/xi) –условные вероятности.
Меньшее значение полной энтропии координат цвета будет
говорить о большей упорядоченности и определенности в цветовой окраске зерна
или крупы, а также ее однородности и отдаленности от состояния равновероятности
появления того или иного сочетания координат х и у.
Во многих случаях, в том числе и
для сравнительной оценки по цветовому признаку качества крупы, выработанной с
применением различных способов ГТО зерна, могут быть использованы и другие,
известные и табулированные в математической статистике критерии, к которым
можно отнести t-критерий Стьюдента существенности
различий преобладающих цветов по вычисленным значениям средних значений
координат цвета ![]() и
и ![]() , F-критерий
Фишера существенности различия между двумя выборочными дисперсиями, критерий
однородности нескольких дисперсий Бартлета М
и критерий существенности различия коэффициентов вариации tф. В первом случае необходимо
вычислить t-статистику
по формуле (на примере координаты х)
, F-критерий
Фишера существенности различия между двумя выборочными дисперсиями, критерий
однородности нескольких дисперсий Бартлета М
и критерий существенности различия коэффициентов вариации tф. В первом случае необходимо
вычислить t-статистику
по формуле (на примере координаты х)
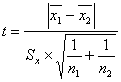 , (5)
, (5)
где ![]() и
и ![]() – средние значения координаты цвета х одной и другой выборки;
– средние значения координаты цвета х одной и другой выборки;
n1 и n2 – число произведенных
измерений для одной и другой выборки;
Sx – среднеквадратическое отклонение, определяемое для
обоих координат по формуле
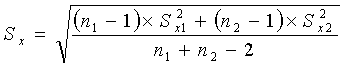 , (6)
, (6)
где ![]() и
и ![]() – дисперсии координаты х одной
и другой выборок.
– дисперсии координаты х одной
и другой выборок.
Статистику t сопоставляют с критическим
значением tкр, находимым из таблиц для уровня значимости α=0,05 и числе степеней свободы n1+n2-2. При t£tкр гипотезу о равенстве координат не
отвергают, а в противном случае бракуют.
Аналогично можно определить и
существенность различия средних значений координат у для двух выборок.
Критерий Фишера F можно вычислить в общем виде по формуле
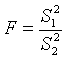 (7)
(7)
где ![]() – большая из двух
дисперсий одноименных координат цвета.
– большая из двух
дисперсий одноименных координат цвета.
Найдя из таблиц значение Fт при степенях свободы k1=n1-1 и k2=n2-1 и сравнивая его с F определяют при уровне значимости a=0,05 существенность различий между![]() и
и ![]() . Если F>Fт то с вероятностью более 0,95 гипотеза о равенстве
дисперсий отвергается и расхождение дисперсий считается существенным, в
противном случае принимается обратное решение.
. Если F>Fт то с вероятностью более 0,95 гипотеза о равенстве
дисперсий отвергается и расхождение дисперсий считается существенным, в
противном случае принимается обратное решение.
М-критерий Бартлета, основанный на предположении о нормальности
(или близости к ней) распределения исследуемого признака в выборках с n>50, для
которых исчислены дисперсии, определяется по величине соотношения М/С, в котором
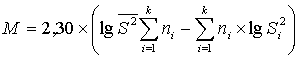 , (8)
, (8)
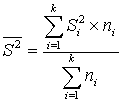 (9)
(9)
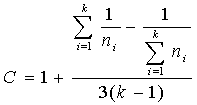 (10)
(10)
В
этих выражениях
Si2 – частная дисперсия координат цвета х или у;
![]() – взвешенная средняя арифметическая дисперсия той или иной
координаты цвета;
– взвешенная средняя арифметическая дисперсия той или иной
координаты цвета;
k – число
анализируемых дисперсий.
Найдя табличное значение критерия ![]() при α=0,05 и m-1 степенях
свободы [1] сравнивают его с фактическим значением соотношения М/С. Если последнее меньше табличного,
то дисперсии различаются незначимо. В противном случае дисперсии признаются
неоднородными.
при α=0,05 и m-1 степенях
свободы [1] сравнивают его с фактическим значением соотношения М/С. Если последнее меньше табличного,
то дисперсии различаются незначимо. В противном случае дисперсии признаются
неоднородными.
Вывод о существенности различия того или
иного статистического показателя при парных сравнениях хотя бы для одной
координаты цвета можно считать достаточным для оценки различия качества
исследуемых выборок и партий крупы, по цветовому признаку.
Таким образом, нами предложены параметры,
характеризующие равномерность гидротермической обработки зерна гречихи. В
качестве параметров качества можно использовать среднеквадратичные отклонения Sх, Sу; дисперсию Sх2, Sу2; коэффициенты вариации Vх, Vу его координат; полной энтропии Н(у/х); t-критерий Стьюдента существенности
различий преобладающих цветов по вычисленным значениям средних значений
координат цвета ![]() и
и ![]() ; F-критерий
Фишера существенности различия между двумя выборочными дисперсиями; критерий
однородности нескольких дисперсий Бартлета М
и критерий существенности различия коэффициентов вариации tф.
; F-критерий
Фишера существенности различия между двумя выборочными дисперсиями; критерий
однородности нескольких дисперсий Бартлета М
и критерий существенности различия коэффициентов вариации tф.
Литература:
1. Венецкий И.Г., Венецкая
В.И. Основные математико-статистические понятия и формулы в экономическом
анализе – М.: Статистика, 1979. – 147 с.
2. Ликеш И., Ляга
Й. Основные таблицы математической статистики - Финансы и статистика, 1985. -
356 с.